目录
博主算法不太好,只做过一百多道题,一个蓝桥杯让我复习了一段时间算法,下面是总结的一些函数等要点做一个备忘录。
并查集的一个题,主要看节点怎么造的,然后如何深搜并给每个节点
辗转相除法求最大公约数 余数是几就再除以几,直到余数为0,最后一个被除以的数即为最大公约数
C++中 string 转 int (stoi 函数和 atoi 函数)
C++中 int 转 string (to_string 函数的使用)
C++中批量递增 vector 的元素 (iota 函数的使用)
注意!初始化vector如果给大小的话用sort排时会把未赋值的0也算进去
重要!string的sort规则,也就是string类型的比大小规则
C++中利用二分法找到下界和上界的方法 (upper_bound 与 lower_bound)
C++中找到 vector 中最大数或最小数的函数 (max_element,min_element)
GCC 自带的内建函数 (__builtin_clz 和__builtin_ctz)
博主算法不太好,只做过一百多道题,一个蓝桥杯让我复习了一段时间算法,下面是总结的一些函数等要点做一个备忘录。
算法笔记
记录没时间学的,比较难的算法
树上启发式合并:用于解决树上求每个结点子树信息的问题。
莫队算法:解决数组上的一些问题,类似暴力但是很多剪枝省时间
求异或和技巧:拆位,一个数组,互相直接两两异或并求和,直接暴力会超时。


**这个乘法定理在草纸上验算了是对的,就是你直接把某一位的0的总数乘上某一位1的总数得到的结果就是这一位上所有数字异或后的和了。**比如某一位的几个数分别是110,1有两个0有1个,则2*1=2.而110互相异或然后和也为2;

记住吧,有点难推。
[先来个蓝桥杯小技巧] excel的使用
向上取整int( (A+B-1)/B )
算法比赛开数组
结论:任何函数里面不要开大数组。
原因:
写在main()外面的变量叫做全局变量,分配在静态数据区。
new出来的变量叫动态变量,分配在堆上。
函数里面的变量叫局部变量,分配在栈上。
前两者基本只受你的内存大小影响,想开多大开多大。
栈空间是和操作系统以及编译器有关的,你用的DevCpp和Windows,那这个限制应该是4MB(如果没有记错的话),int[5000000]需要的空间是19MB,所以就放不下(俗称爆栈),从而就运行错误了。
当然,如果你硬是想把这个数组放在函数里面,可以通过调整编译选项来达到。
点DevCpp上面的'compiler option', 把这段话贴到'add these commands to compiler'的那个框里:
-Wl,--stack,100000000
所以开数组直接开在main外面就行了。
常用容器(包括priority_queue大顶堆)
并查集的一个题,主要看节点怎么造的,然后如何深搜并给每个节点
辗转相除法求最大公约数 余数是几就再除以几,直到余数为0,最后一个被除以的数即为最大公约数

最小公倍数:为两数乘积除以最大公约数
C++中vector的函数传递
void dfs(int i,vector<T> &t) //引用传递
vector<T> t(n+1);
dfs(1,t);
C++中 string 转 int (stoi 函数和 atoi 函数)
string a="adwas15641";
int get=stoi(a.substr(5,5)); //从第5个开始,向后截取5个字符作为新的字符串,并用stoi转换为int类型
//get为15641
string a="adwas15641";
int get=atoi(a.substr(5,5).c_str()); //atoi内的参数是const *char类型,所以必须用.c_str()将string转化为const char*类型,内容与string一致
//get为15641,效果一样运算符中**&&比||优先级高**
取绝对值 abs(n);
C++中将string串逆序
chuan=string(chuan.rbegin(),chuan.rend());
//利用string构造函数,传入原字符串逆向迭代器
C++中 int 转 string (to_string 函数的使用)
int a=123;
string get=to_string(a); //用于将数字常量转换为string类型
//get为字符串123
//对于负数,输出会带负号
int a=-123;
string get=to_string(a); //用于将数字常量转换为string类型
//get为字符串-123
C++中批量递增 vector 的元素 (iota 函数的使用)
vector<int> indices(n);
iota(indices.begin(), indices.end(), 0); //使indices从0开始递增,每次加1
//indices: 0,1,2,3,4,5....n-1
sort(indices.begin(), indices.end(), [&](int a, int b) {
return persons[a] < persons[b]; //小的在前面
//也可以这样写 if(persons[a] < persons[b]) return 1;
}); //此处和sort共用可以用indices中的值来表示persons[]中从小到大排序的关系。-
这种用法是一种不改变 persons 数组中顺序的前提下得到其中顺序的方法。 非常有用!
排序函数sort用法
//需要的头文件
#include<algorithm>
//使用方式
sort(首元素地址(必填),尾元素地址(必填),cmp(比较函数,非必填));
//默认为升序排序,如果想从大到小排
sort(a.begin(),a.end(),greater<int>());
//cmp比较函数
bool cmp(int a,int b)
{
return a>b;
} //从大到小排,若不加cmp则默认升序排注意,sort(a.begin(),a.end(),cmp) 这里cmp不写参数
注意!初始化vector如果给大小的话用sort排时会把未赋值的0也算进去
重要!string的sort规则,也就是string类型的比大小规则
先比第一个字符,如果相同则比第二个字符,若一个有第二个字符一个没有,则有第二个字符的大
比如把7,13,4,246排序成7,4,246,13
**但是!**98,9会被排成98 9 但是989<998
321,32会被排成321,32 但是32321>32132
比较这种时一定记得比较a+b和b+a如下。
bool cmp(string a,string b)
{
return a+b>b+a;//如果a+b>b+a,则把a排在前面,否则将b排在前面
}C++中利用二分法找到下界和上界的方法 (upper_bound 与 lower_bound)
vector<int> a;
int x; //x是要找的目标值
//赋值后
// 升序数组中:
upper_bound(a.begin(), a.end(), x); // 查找第一个 > x的元素的地址
lower_bound(a.begin(), a.end(), x); // 查找第一个 >= x的元素的地址
// 降序数组中:
upper_bound(a.begin(), a.end(), x, greater<type>()); // 查找第一个 < x的元素的地址
lower_bound(a.begin(), a.end(), x, greater<type>()); // 查找第一个 <= x的元素的地址
//上式返回的是找到的元素的地址,若想获得值可以加*,如下,若想获得下标则可以-a,如下
int kkk=*upper_bound(a.begin(), a.end(), 5); //获得第一个 >5的元素的值
int kkk=upper_bound(a.begin(), a.end(), 5)-a; //获得第一个 >5的元素的下标
//lower_bound同理C++中找到 vector 中最大数或最小数的函数 (max_element,min_element)
int mx=*max_element(a.begin(),a.end()); //因为max_element获得的是最大值的地址,所以进行取值操作,取下标可以-a
int mx=max_element(a.begin(),a.end())-a; //取下标
//取最小值同理GCC 自带的内建函数 (__builtin_clz 和__builtin_ctz)
__builtin_clz(mx) //用于获取mx中二进制从左往右连续的0的个数
//mx是一个int类型32位的数,利用下面这个可以获得mx这个数最高位右边有多少位
32-__builtin_clz(mx)-1
//比如mx为10,二进制为0000 0000 0000 0000 0000 0000 1010
int high_bit=32-__builtin_clz(mx)-1; //high_bit的值为3,即为最高位1右边的位数
// __builtin_clz(mx)得到的值为24__builtin_ctz(mx) //用于获取mx中二进制从右往左连续的0的个数
//mx是一个int类型32位的数
//比如mx为8,二进制为0000 0000 0000 0000 0000 0000 1000
// __builtin_ctz(mx)得到的值为3-
如果题目中需要用到位运算,可以思考能否利用上面这个函数进行辅助。
重拾算法(哭
字母一个有26个
ascll码中,A为65,a为97。大小写之间相差32
数字0为48,数字在字母前面!
大写转小写:str[i] = tolower(str[i]);
小写转大写:str[i] = toupper(str[i]);
substr是C++中string类的成员函数,用于从一个字符串中提取子字符串。
其语法如下:
string substr(size_t pos = 0, size_t count = npos) const;其中,pos表示子字符串的起始位置,count表示要提取的字符数。
-
如果只提供
pos参数,则从位置pos开始一直提取到原字符串的末尾。 -
如果同时提供了
pos和count参数,则从位置pos开始提取count个字符。
示例:
string str = "Hello, World!";
string sub1 = str.substr(7); // 从位置7开始提取子字符串,结果为"World!"
string sub2 = str.substr(0, 5); // 从位置0开始提取5个字符,结果为"Hello"注意:substr返回的是提取的子字符串,原字符串不会被修改。
pair&set&map
重拾算法(哈希表STL
哈希表的创建:
//创建哈希表,可以用key来寻找value的值或位置等,查询时间复杂度为O(1)
unordered_map<key,value> Hash{{1,10},{2,12},{3,13}}; //也可以不带后面那些默认值
//或者用另一个哈希表来赋初值
unordered_map<key,value> Hash_2(Hash);//直接复制上面那个哈希表哈希表的插入:
//可以直接用下标的方法插入
Hash[a]=b; //直接将key为a的位置赋值为b,此方法会覆盖之前该位置的value
//可以用insert的方法插入
Hash.insert({a,b}); //将key为a的位置的值赋为b,此方法不会覆盖之前该位置的value,所以原来有值时值不会变键值对的删除:
//使用erase函数
unordered_map<int, int> hmap{ {1,10},{2,12},{3,13} };
unordered_map<int, int>::iterator iter_begin = hmap.begin();
unordered_map<int, int>::iterator iter_end = hmap.end();
hmap.erase(iter_begin); //删除开始位置的元素
hmap.erase(iter_begin, iter_end); //删除开始位置和结束位置之间的元素
hmap.erase(3); //删除key==3的键值对哈希表的查询:
//直接用key查询
int value=Hash[a]; //注意,若a不存时会创建key为a,value为默认值(0)的键值对
//用at查询
int value=Hash.at(a); //注意,若a不存在时会报错,所以必须确保这个key存在
//用迭代器查询
for(auto it=Hash.begin();it!=Hash.end();it++)
{
if(it->first==a)
if(it->second==b) //可以查key也可以查value
//用迭代器it进行循环操作,执行查询等操作
}
迭代器的使用
//用迭代器
unordered_map<int,int>::iterator iter=Hash.begin(); //指向第一个键值对
iter->first; //为第一个值的key
iter->second; //为第一个值的value
unordered_map<int,int>::iterator iter=Hash.end(); //指向最后一个键值对的下一个位置,所以是空
//判断某key的哈希表是否存在时:
auto nb=Hash.find(key);
if(nb!=Hash.end()) //若这个符合,则存在
{
return true; //存在
}
//循环查询时
for(auto it=Hash.begin();it!=Hash.end();it++)
{
//用迭代器it进行循环操作,执行查询等操作
}查看是否存在某key
//用count
int count = Hash.count(key); //若key不存在,则返回0,若存在则返回1,因为哈希表中每个key只有一个
//用find
auto nb=Hash.find(key);
if(nb!=Hash.end()) //若这个符合,则存在
{
return true; //存在
}队列
queue<T> QU;
/*队列的一些常用函数*/
queue.push(value); ///< 在队列队尾插入元素value
queue.pop(); ///< 弹出队头
queue.empty(); ///< 判断队列是否为空,如果为空返回真,否则返回假
queue.size(); ///< 返回队列的长度
queue.front(); ///< 返回队头元素
queue.back(); ///< 返回队尾元素前缀和基础
前缀和与差分
模运算
mod(a,b)相当于a%b,a/b取余,结果的符号和b看齐
函数:fmod(-10, 3)
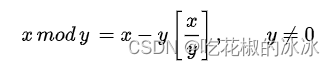
取余运算
rem(a,b)相当于a/b取余,结果的符合向a看齐
函数:a%b
与、或、异或运算
负数用补码参与运算 (补码为所有位置反,末位+1)
按位与运算符(&)
运算规则:0&0=0; 0&1=0; 1&0=0; 1&1=1;
即:两位同时为“1”,结果才为“1”,否则为0
// 3&5 即 0000 0011 & 0000 0101 = 0000 0001 因此,3&5的值得1
//-3 & 5即 1111 1101 & 0000 0101 = 0000 0101 因此,-3 & 5的值得5
与运算小技巧
若想使某数清零,只要与一个各位都为零的数值相与,结果为0
3 & 0=0;
按位或运算符(|)
运算规则:0|0=0; 0|1=1; 1|0=1; 1|1=1;
即 :参加运算的两个对象只要有一个为1,其值为1。
// 3|5 即 0000 0011 | 0000 0101 = 0000 0111 因此,3|5的值得7
“或运算”的小技巧
常用来将数据的 指定位 置为1。
例:将X=10100000的低4位置1 ,用 X | 0000 1111 = 1010 1111即可得到。
异或运算符(^)
参加运算的两个数据,按二进制位进行“异或”运算。
运算规则:0^0=0; 0^1=1; 1^0=1; 1^1=0;
即:参加运算的两个对象,如果两个相应位为“异”(值不同),则该位结果为1,否则为0。
“异或运算”的小技巧: (1)使特定位翻转 找一个数,对应X要翻转的各位,该数的对应位为1,其余位为零,此数与X对应位异或即可。 例:X=10101110,使X低4位翻转,用X ^ 0000 1111 = 1010 0001即可得到。
(2)与0相异或,保留原值 ,X ^ 0000 0000 = 1010 1110。 从上面的例题可以清楚的看到这一点。
树状数组的更新操作
表达式 i & -i 通常用于获取 i 的最低位的 1 所代表的值。这是因为 -i 是 i 的二进制表示的按位取反加 1,其结果仅保留了 i 的最低位的 1,其余位全部置为 0。
举个例子,假设 i = 6,其二进制表示为 110,那么 -i 的二进制表示为 010。则 i & -i 的结果为 010,即 2。
这个操作通常用于位运算中的一些算法中,比如在树状数组或者二进制索引树(Binary Indexed Tree)中用于获取节点的父节点,或者在寻找数组中的某个数的最后一位 1 的位置时。
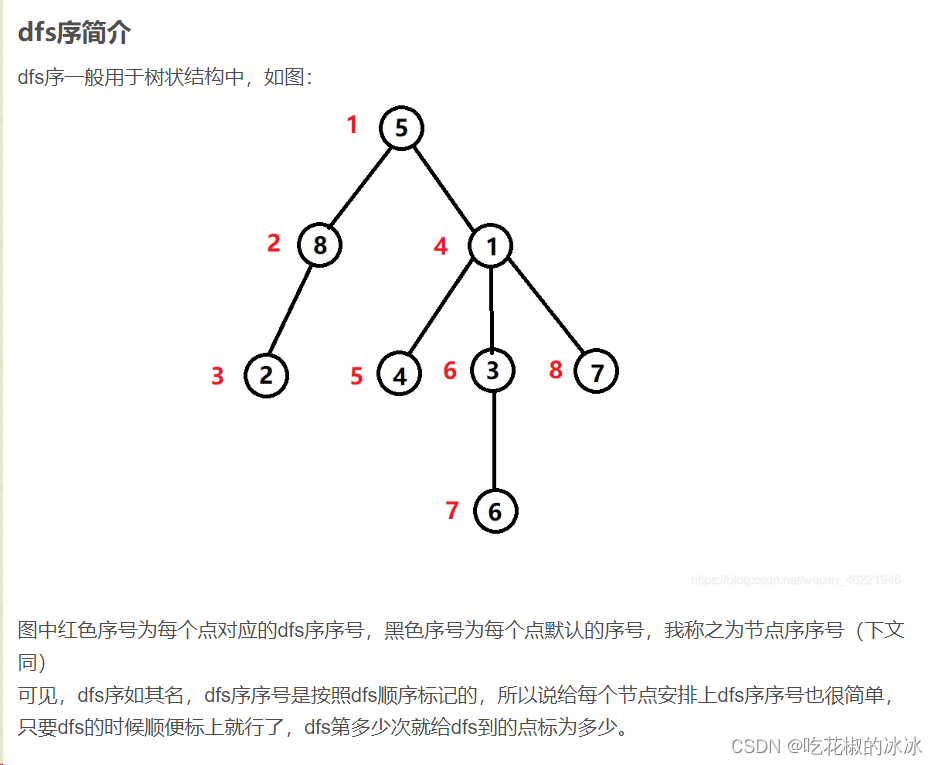
dfs序(这块抄别人的了,因为他写的太好了

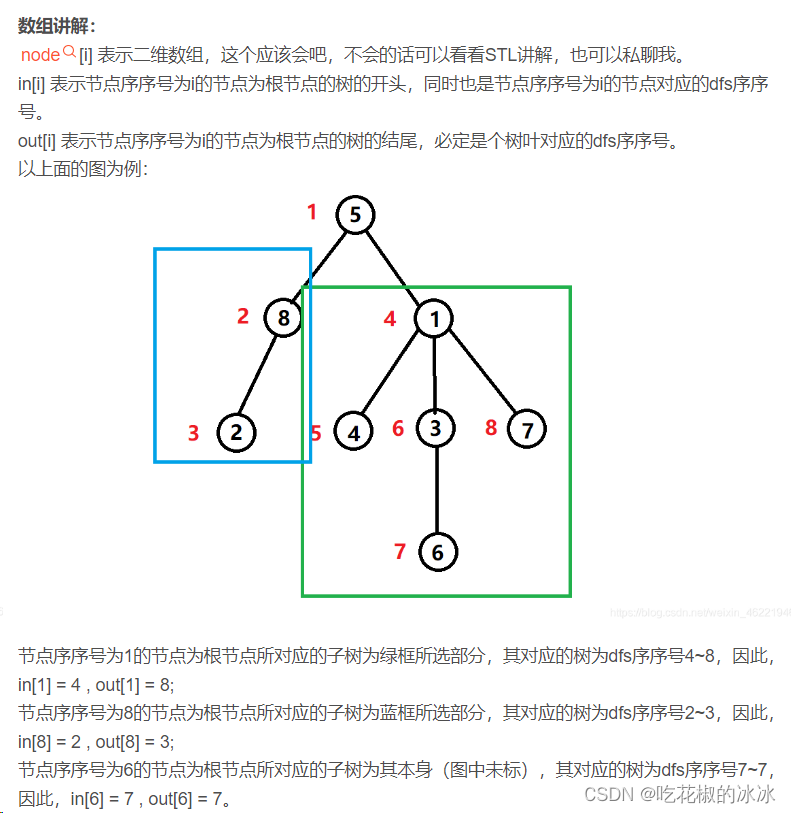


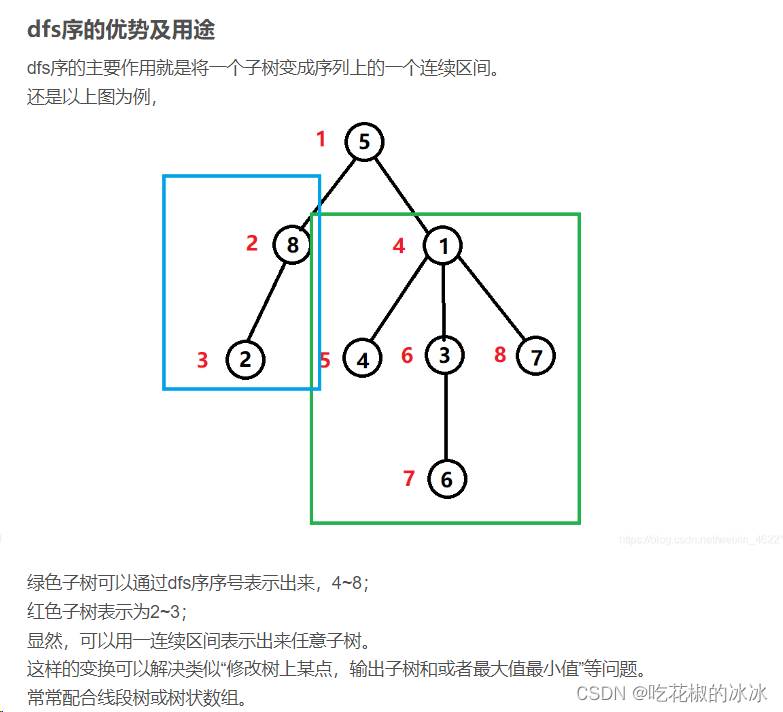
线段树
这个博客抄了很多其他的博客,这里无法一一列举




 本文是一篇算法复习笔记,涵盖了C++中的各种函数、数据结构(如并查集、优先队列、哈希表、线段树等),以及排序、位运算、树状数组和DFS序等内容,旨在帮助记忆和理解算法竞赛中的关键知识点。
本文是一篇算法复习笔记,涵盖了C++中的各种函数、数据结构(如并查集、优先队列、哈希表、线段树等),以及排序、位运算、树状数组和DFS序等内容,旨在帮助记忆和理解算法竞赛中的关键知识点。
















 3485
3485

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








