什么是反向传播算法

反向传播算法（Backpropagation）是一种训练神经网络的核心算法，用于计算并调整网络中每个参数（如权重和偏置）的梯度，以最小化预测输出与真实值之间的误差。反向传播通过链式法则计算每层参数的梯度，然后利用这些梯度更新权重，以便神经网络逐步优化和收敛。

反向传播算法的基本步骤

反向传播算法的步骤包括前向传播、误差计算和反向传播三个主要阶段。

1. 前向传播（Forward Propagation）

• 输入数据经过网络层层传递，经过每一层的权重和偏置的加权处理以及激活函数的变换，最终得到输出。
• 输出结果与真实值之间的误差即是我们要优化的对象。

2. 误差计算（Calculate Loss）

• 使用损失函数计算模型预测输出与真实值之间的误差，例如常用的均方误差（MSE）或交叉熵损失。
• 损失值越大，说明模型预测结果与真实值偏差越大。

3. 反向传播（Backward Propagation）

• 计算梯度：通过链式法则，反向计算每个参数对损失的导数（即梯度）。从输出层开始，逐层向前回溯，直到输入层。
• 更新参数：利用计算出的梯度，用优化算法（如梯度下降）更新每层的权重和偏置，使得损失值逐步减小。

反向传播的具体原理

举例说明

例1

假设有一个函数 其中x=-2,y=5,z=-4

那么将其拆成线性处理得到：

我们成从左到右的计算过程为前向传播，

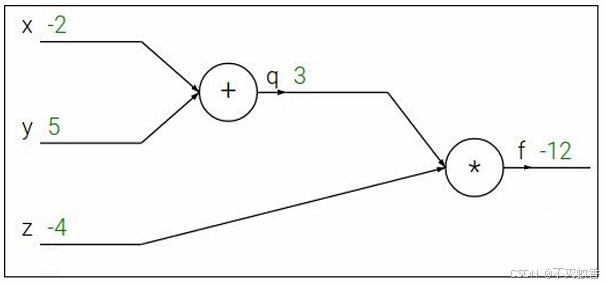
添加节点名称，并对每个结点求偏导得到上图。

那么怎么求，初始变量x、y、z的偏导数呢。

先求出最后面的偏导，第一个对原函数的偏导数永远是1。

然后依次反向求偏导。

然后当求到对y求偏导数的时候发现，f对y的偏导数其实等于f对q的偏导数乘上q对y的偏导数。

这里我们将f对q的偏导数成为远端梯度，f对q的偏导数成为本地梯度。

后面对x的偏导数也能验证这一结果，所以根据求导的链式法则，所有的偏导数都可以这么求，用远端梯度乘以本地梯度，就能得到总体的梯度。

例2

有一个函数

展开后：

反向传播：

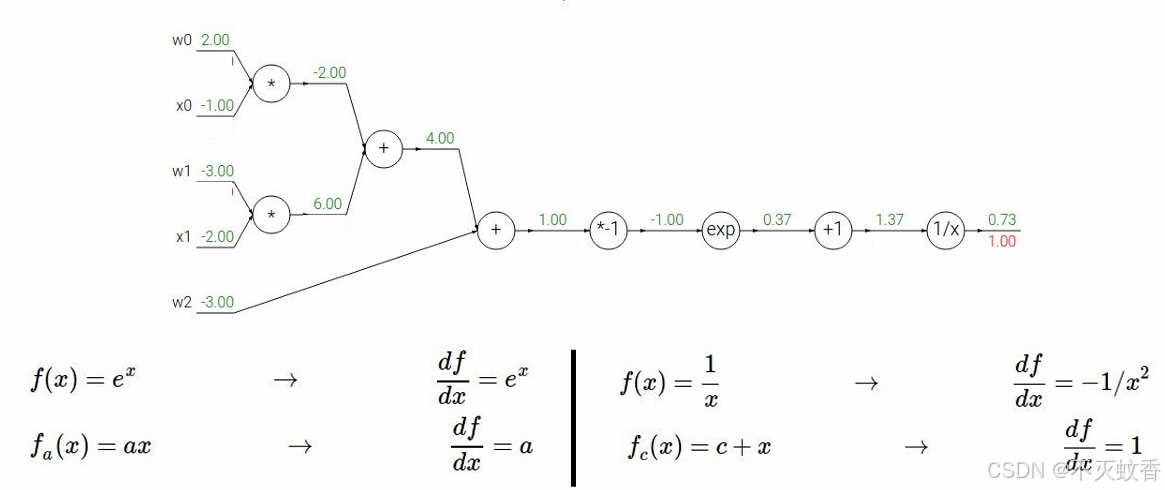
到此一个复杂函数求导验证完成。

总结：

每次计算只关注本地梯度，整个问题就会变的很简单，多复杂的公式都可以用反向传播来求导数。

反向传播的优缺点

优点：

• 高效的训练：反向传播算法能够快速计算出参数的梯度，显著提高训练速度。
• 通用性强：可适用于几乎所有类型的前馈神经网络，简单适应多层网络。

缺点：

• 梯度消失/爆炸：在深层神经网络或长时间序列中，梯度可能会在传播中变得非常小（梯度消失）或非常大（梯度爆炸），导致模型难以收敛。
• 依赖大量数据：反向传播的效果在数据量大的情况下更好，数据不足时可能会导致过拟合。

反向传播算法是现代神经网络训练的基础，其改进版本和优化算法广泛用于各种深度学习任务中。