深度优先解决搬动积木块问题python

首先我们来看题目，题目要求我们对初始状态到目标状态进行求解，我们对初始状态分析可得

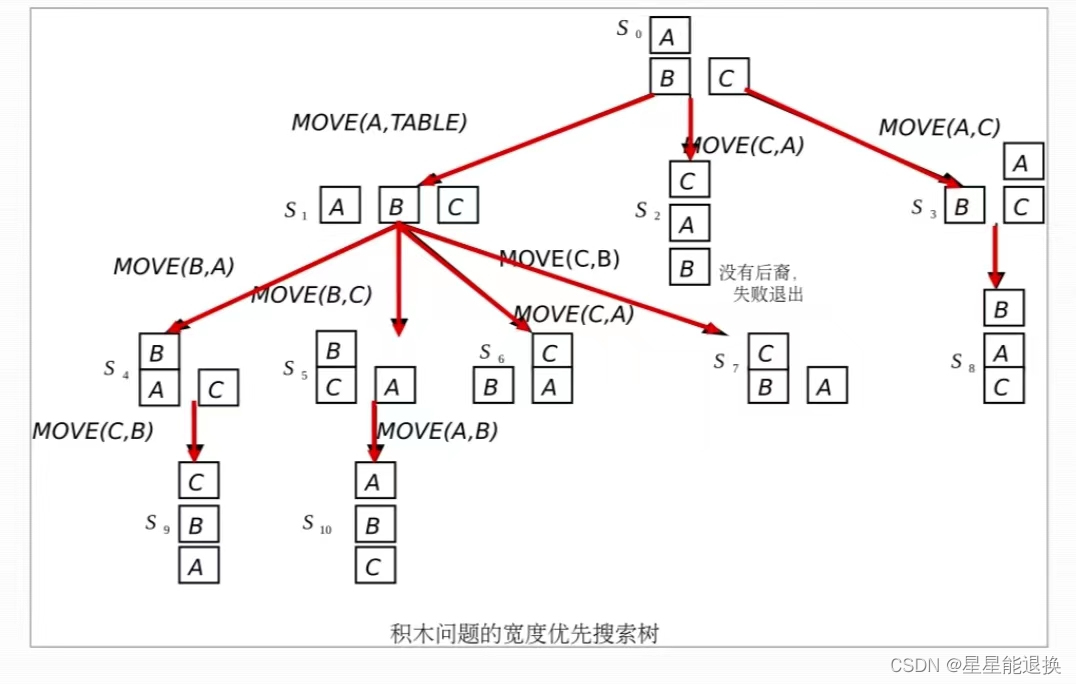
 把该搜索策略的过程构建为多叉树

 

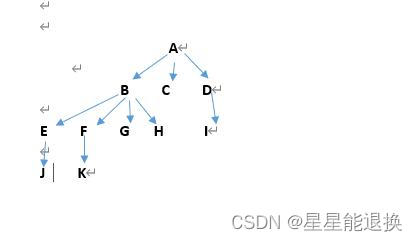
 那么根据题目要求，我们能知道从初始状态到目标状态的过程就是从状态A到状态K的过程，

求解思路为

1.传入start 和 end 两个 目标值

2. 找到从根节点到目标节点的路径

3. 从所在路径，寻找最近的公共祖先节点，

4. 对最近公共祖先根节点 拼接路径

import copy

#节点数据结构
class Node(object):
    def __init__(self,value=None):#初始化节点
        self.value = value#节点值
        self.child_list = []#子节点列表
    def add_child(self,node):
        self.child_list.append(node) #添加子节点
'''构建多叉树
                 A
        B        C        D
    E  F  G  H            I
    J  K
'''
def init():
    root = Node('A')
    B = Node('B')
    root.add_child(B)
    root.add_child(Node('C'))
    D = Node('D')
    root.add_child(D)
    E = Node('E')
    B.add_child(E)
    F = Node('F')
    B.add_child(F)
    B.add_child(Node('G'))
    B.add_child(Node('H'))
    D.add_child(Node('I'))
    E.add_child(Node('J'))
    F.add_child(Node('K'))
    return root


def deep_first_search(cur,val,path=[]):#深度优先，找到从初始状态到目标状态的路径
    path.append(cur.value)   #当前节点值添加到路径
    if cur.value == val:   #判断是否找到目标值，如果找到则返回该路径
        return path
    if cur.child_list == []:#判断子节点列表是否为空
        return 'no'
    for node in cur.child_list:  #对子列表里的每个每个子节点进行递归
        t_path = copy.deepcopy(path) #将临时路径path拷贝到t-path
        res = deep_first_search(node,val,t_path)
        if res == 'no':   #判断是否为no,如果是则继续寻找子节点
            continue     #终止本次循环
        else:
            return res  #如果不是no，则说明找到了路径，返回res
    return 'no'
'''输入两个目标值start和end，找到从根节点到目标节点的路径，然后找到两条路径的公共父节点，将两条路径进行合并'''
def get_shortest_path( start,end ):
    path1 = deep_first_search(root, start, [])
    path2 = deep_first_search(root, end, [])
    if path1 == 'no' or path2 == 'no':
        return '无穷大','无节点'     #
    #两条路径从后向前找公共父节点
    len1,len2 = len(path1),len(path2)
    for i in range(len1-1,-1,-1):
        if path1[i] in path2:
            index = path2.index(path1[i])
            path2 = path2[index:]
            path1 = path1[-1:i:-1]
        break
    res = path1+path2 #目标路径
    length = len(res)
    path = '->'.join(res)#将路径进行合并
    return '%s:%s'%(length,path)
if __name__=='__main__':
    root=init()
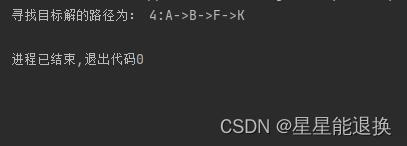
    res = get_shortest_path('A','K')
    print("寻找目标解的路径为：",res)

运行结果为

 本题解题灵感来自https://blog.youkuaiyun.com/weixin_30905133/article/details/96071969