第六次作业

一阶系统的频率响应

对于一阶系统，当传递函数为线性函数G（s），当s=jw，输入函数为Misin（wt+Φi），输出函数为M0sin（wt+Φ0）

推导用到拉普拉斯变换以及逆变换，可得频率响应就是稳态响应。在利用欧拉公式思想反代，得到下面图片公式

重要公式：

1、Mo/Mi=M（振幅响应）

2、Φ0-Φi=Φ（相位响应）

 

常见传递函数，G（s）=a/（s+a），令s=jw，通过一系列推导，得到如图公式：

 当w=a，我们称之为截至频率，

频率增加，振幅降低，称为低通滤波器

当上图公式w与a互换位置时，

频率增加，振幅降低，称为高通滤波器

二级系统的频率相应

常见现象：共振效应

对于二阶系统，当传递函数为线性函数G（s），当s=jw，输入函数为Misin（wt+Φi），输出函数为M0sin（wt+Φ0）

 

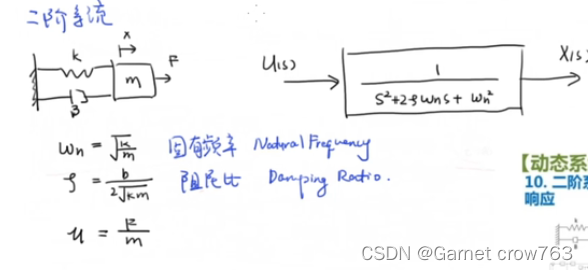
G（s）=wn方/（s方+2*wn*S*ε+wn方）

Ω= 输出频率/系统固有频率

 当系统达到共振频率时，

 

对于阻尼比系统比较小的情况下，系统会表现强烈的振幅反应

自动控制-根轨迹

“根”约等于“极点”

对于一般一阶系统，G（s）为上方函数，根等于-a

对于根的位置（重要指标），影响着系统时间常数等

对于二级系统，

对于跟的位置（重要指标），影响着系统的上升时间等

对于更高阶，拆开分析即可

根轨迹的几何性质：

常见形式：

判断跟是否在根轨迹上：