这节课会介绍一些基本的概念,并结合例子讲解。
在马尔科夫决策框架下介绍这些概念
本博客是基于西湖大学强化学习课程的视屏进行笔记的,这是链接:
课程链接
强化学习的基本概念
网格世界:

世界由边界以及不同的区域组成:可进入、障碍、目的。
这个例子能很好的理解概念。在
grid-world的例子中,强化学习的目的是找到一个比较好的路径到达目标。
要解决这个问题,有一个比较核心的问题是:我如何评价这个路径是好还是坏。
直观上的评价:要避免forbidden,不要由没有必要的拐弯,不要试图超越边界等等。
state和state space

state在这里就对应了一个网格的位置(在x方向上的,在y方向上的)。这个state其实算是一个比较简单的state了,如果agent是一个机器人的话state可能还需要包括速度、加速度等等。
State space:状态空间,其实就是状态总的一个集合,用花括号来表示。后面的数字表示i的范围。
Action和Action Space
下一个概念ACtion:在每一个状态中,都有一系列可以采取的行动。在这里Action就有五个可以选择的动作,如图。

Action Space:就是在某个状态下,所有可能得action的集合。这里需要注意的是,Action Space和状态是依赖的。
途中A(Si)这种写法也表示了它其实是一个函数。
State transition
当采取了一个状态的时候,agent有可能会从一个状态移动到另一个状态中去,这样的过程就叫
状态转移。状态转移其实是
定义了agent和环境交互的行为。
在forbidden area的定义有两种可能:
- forbidden area可以进入,但是进入这个区域会被惩罚
- forbidden area不可以进去
我们这节课选择的是第一种解释方式。

这种解释方式有可能会带来一些比较有意思的情况出现:agent为了更快地达到target有可能会冒险进入forbidden area。
我们可以通过表格的方式来表示状态转移。
但是这种表达方式在日常使用中是比较受限的。因为这种表达方式只能表达一些determine的状态,但是有很多种情况是表示不出来的,比如说s7往下走被弹回了s1。
这时候我们引入state trainsition probability(条件概率)。这是第一次引入probablity来描述状态转移。
图中的两种表达方式就是
直观与数学的表达方式的区别。

这里提到了一个比较重要的数学基础————
条件变量(概率论),需要去学习一下基础的概念。
其实意思就是,在s1时tack a2时跳到s2的概率是1。
虽然这里采取的还是确定性的例子来解释,但是条件概率还可以形容一些随机性的例子,比如说有一股风从上往下吹,这样s1 tack a2就有50%的概率到s2还有50%的概率到s5。
Policy
Policy会告诉agent在某个状态会采取什么action
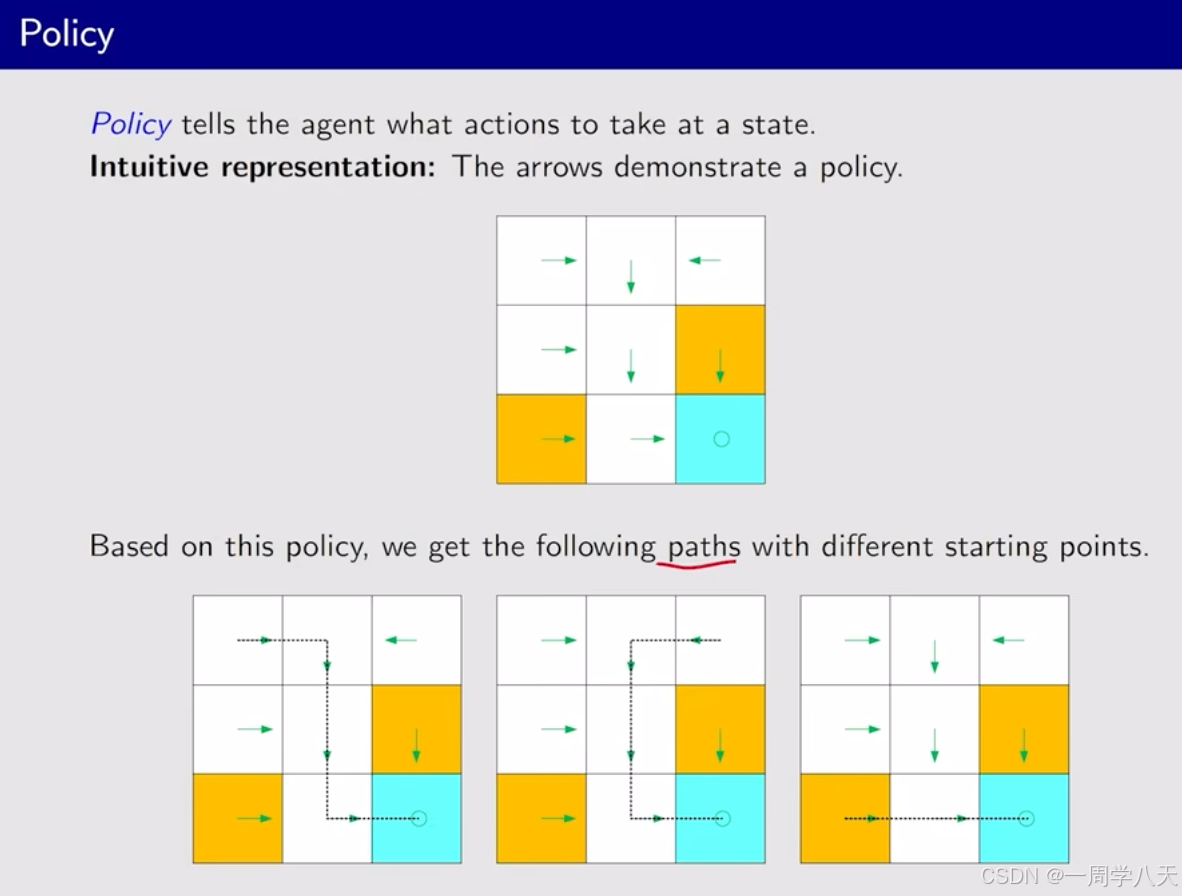
上面那一张图其实就是一个策略,在不同的格子采取不同的action,最终目的都是达到最后的target。根据这个策略不论在哪个格子出生都能到达target。
用数学的语言描述Policy,可以通过条件概率来表示Policy:
再次提到确定性:
在这里确定性的意思是——在s1状态下一定会采取a2的动作。
相对的就有不确定的情况,通过条件概率能够很好的理解。
在s1中采取a2和a3的概率都是0.5
策略也是可以通过表格的方式表现出来:
这个表格是非常general的,能够表达确定性的和随机性的情况。实际上在编程的方式——就可以通过矩阵的方式来封装这些数据,达到表示这个策略的效果。然后在选取策略的时候,去一个在0~1之间的随机数就可以了,然后通过这个随机数落在的区间来确定最后采取的action。
Reward
是一个非常独特性的概念。
首相他是一个标量:正数表示鼓励这个行为;负数表示惩罚这个行为。
如果这个值为0意味着什么?意味着没有punishment,没有punishment就意味着一定程度上的鼓励(有点像法无禁止皆可为)
我们可以对一些情况设计一些reward值:超出边界就-1,进入forbidden area就-1,到达target就+1。
我们可以把
设置reward值当做是人机交互的一种手段。我们可以引导agent,它应该怎么做不应该怎么做。
通过表格来表示不同state下采取不同action的影响:
这个表格
适用性不广泛,还是因为确定性问题。实际情况下得到的
reward不一定是确定的。
这也就意味着不能通过矩阵将其简单记录。
这时候我们引入了数学的方式来描述:
条件概率。
敲黑板:我们举出的例子是确定性的,但是奖励转换有可能是不确定的,比如:你努力学习了,一定会获得奖励,但是获得多少奖励是不确定的。
而且奖励是依赖于当前的状态和采取的行动的,而不是下一个状态相关的。
trajectory
是一个state-action-reward链(chain),return是一个tracjectory整个链收集到的reward总和。
Policy不同trajectory也不同
return的作用:通过一个具体的数值,可以用来形容哪个policy更好。而不是人类直观地感受出来的。
Discounted return
trajectory有
可能是无限的。比如在上面的例子中,s9的位置一直在循环的话最后的return是无限的。
为了解决这个问题,引入了discount rate来解决这个问题。
通过调整gama,我们可以控制reward的积累速度。close to 0就积累的慢,close to 1就积累的比较快。
减小gama可以让agent变得近视——也就是让他更注重最近的reward。如果gama比较大的话他就会变得更加远视——更加注重长远的reward。
这里的结果是一个
等比数列求和。
Episode
一个resulting的trajectory被称为一个episode,一个episode通常是有限步的,这样的任务也被称为episodic tasks。
不过有些任务是没有terminal states的,这就意味着有些agent与环境的交互是永远不会结束的。这种任务被称为continuing task。但是在这节课我们不区分episodic和continuing tasks这两种方式,因为我们有两种方法将episodic转化为continuing tasks。
- 将target这一个state的所有action选择改为只有一个action选择——就是在这个状态重复(a5) ,还要再讲这里获得的所有reward都设置为0。这样就实现了将target state转换为absorbing state
- 将target state认为是一个普通的状态。然后选择一个策略,如果策略的结果好的话就会一直重复这个策略,不好的话也可以跳出来。
在我们的课程中,我们采用的是第二种方式,这种方式不会区别对待各种状态。这样也会更一般化。
Markov decision process(MDP)
将我们上面学到的这些概念放入马尔科夫决策框架中去,
这是一个框架。
MDP有很多的要素:第一个要素就是它包含了很多集合。
Sets:
- State:状态集合
- Action:A(s)
- Reward:奖励的集合R(s,a)
第二个要素就是probablity distribution:
- p(s'|s,a)
- p(r|s,a)
第三个要素就是policy:在状态s采取状态a的概率pi(a|s)
第四个要素是马尔科夫性质:memoryless property。一般来说:以前的状态和决策会影响到今天的决策,但是马尔科夫性质定义下一个状态的转换不会与以前的状态、动作有关,只与上一个相关且概率相等。
Markov->Markov property
decision->policy
precess->通过Sets和Probablity distribution来描述,从某个状态跳到某个状态这个过程

























 498
498

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










