数模笔记：拟合算法（最小二乘法）

基本思想：

        拟合问题的目标是寻求一个函数（曲线），使得该曲线在某种准则下与所有的数据点最为接近，即曲线拟合的最好（最小化损失函数）。

        与插值问题不同，在拟合问题中不需要曲线一定经过给定的点。

具体步骤：

        1、确定拟合曲线（比如y=kx+b）

        2、用最小二乘法求解参数k和b（yihat是拟合值，yi是真实值）

                第一种定义:

                        

                 第二种定义：

                     

                第一种定义有绝对值，不容易求导，因此计算比较复杂。

                所以我们往往使用第二种定义，这也正是最小二乘的思想。

                为什么不用四次方？

                (1)避免极端数据对拟合曲线的影响。

                (2)最小二乘法得到的结果和MLE极大似然估计一致。

                     不用奇次方的原因：误差会正负相抵。

                 损失函数:

                       

                分别对k和b求偏导，令其偏导数等于0，解得可以使L取得最小值的(k,b)。

                

        3、利用Matlab的曲线拟合工具箱cftool

 

        4、评价拟合的好坏

                总体平方和SST:

                

                 误差平方和SSE：

                

                 回归平方和SSR：

                

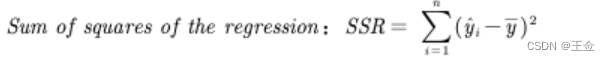
                 可证明：SST=SSE+SSR

                拟合优度:

                

                拟合优度越接近1，说明误差平方和越接近0，误差越小说明拟合越好。

                 注意，R方只能用于拟合函数是线性函数（参数是线性的）时，对于拟合结果的评价。

                非线性函数和其他函数，直接看SSE即可。

 小知识：

        cftool可以画三维拟合图。