二分法（力扣）

二分法

定义

二分法（Bisection method） 即一分为二的方法. 设[a，b]为R的闭区间. 逐次二分法就是造出如下的区间序列([an，bn])：a0=a，b0=b，且对任一自然数n，[an+1，bn+1]或者等于[an，cn]，或者等于[cn，bn]，其中cn表示[an，bn]的中点.

典型算法

算法：当数据量很大适宜采用该方法。采用二分法查找时，数据需是排好序的。
基本思想：假设数据是按升序排序的，对于给定值key，从序列的中间位置k开始比较，
如果当前位置arr[k]值等于key，则查找成功；
若key小于当前位置值arr[k]，则在数列的前半段中查找,arr[low,mid-1]；
若key大于当前位置值arr[k]，则在数列的后半段中继续查找arr[mid+1,high]，
直到找到为止,时间复杂度:O(log(n))

求法

给定精确度ξ,用二分法求函数f(x)零点近似值的步骤如下:
1 确定区间[a,b],验证f(a)·f(b)<0,给定精确度ξ.
2 求区间(a,b)的中点c.
3 计算f©.
(1) 若f©=0,则c就是函数的零点;
(2) 若f(a)·f©<0,则令b=c;
(3) 若f©·f(b)<0,则令a=c.
(4) 判断是否达到精确度ξ:即若|a-b|<ξ,则得到零点近似值a(或b),否则重复2-4
（二分法释义来源于百度）

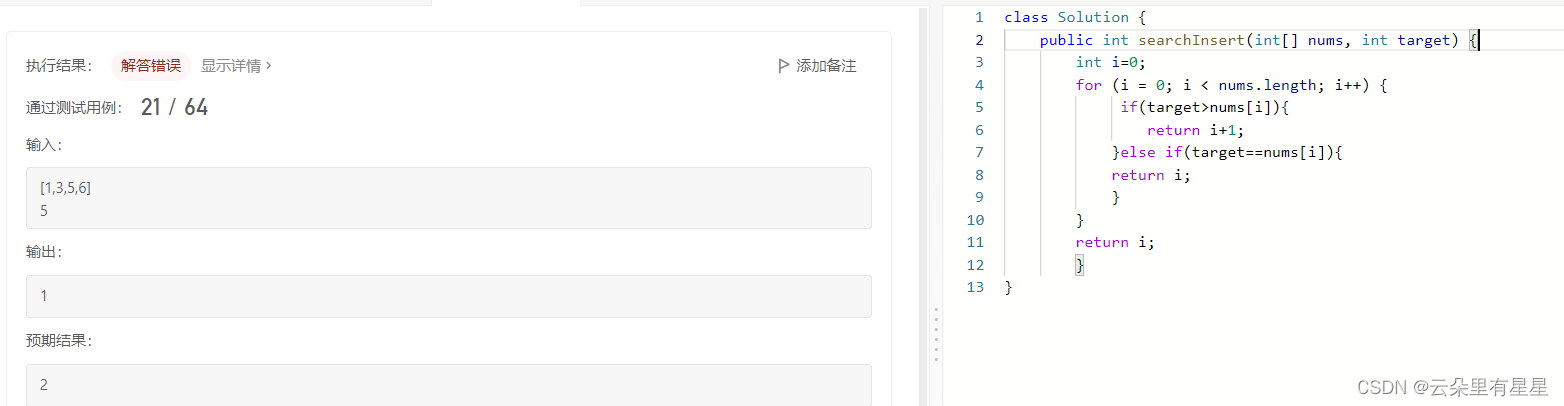
搜索插入位置（35）

题目

题解

官方题解：

class Solution {
	public int searchInsert(int[] nums, int target) {
	    int n = nums.length;
	    int left = 0, right = n - 1, ans = n;
	     while (left <= right) {
	        int mid = ((right - left) >> 1) + left;//(right - left) >> 1相当于(right - left)/2，但位运算符比/运行快
	        if (target <= nums[mid]) {
	             ans = mid;
	             right = mid - 1;
	        } else {
	             left = mid + 1;
	            }
	        }
	        return ans;
	    }
	}

(right - left) >> 1+left与**(right + left) >> 1** 效果一样，但在本题中，前一种写法避免了值超出int型数的范围。

二分查找（704）

题目

官方题解+理解

class Solution {
    public int search(int[] nums, int target) {
    int left=0,right=nums.length-1;
		while(left<=right) {
			int mid=((right-left)>>1)+left;
			if (target==nums[mid]) {//如果目标值等于数组的中间值，表明目标值等于数组下标为mid的数，直接返回
				return mid;
			}else if(target<nums[mid]) {//如果目标值小于数组的中间值，表明目标值在数组下标为[0,mid-1]的范围内
				right=mid-1;
			}else  {//如果目标值大于数组的中间值，表明目标值在数组下标为[mid+1，right]的范围内
				left=mid+1;
			}
		}
		 return -1;       
    }
}