（算法）三道事例让你懂得二分法

简述二分法与常规找排序的不同以及优势

通常我们在寻找一个有序数组中的最大值，或者是找某个数，最常规的做法是遍历，比如从左向右依次比较，时间复杂度为O（N），而使用二分法，则可以将时间复杂度控制到O（logN，log（2，N在这里通常简写为logN））。

第一个简单事例来初步了解

• 在一个有序数组中，寻找到一个指定的数。

（1）常规做法，遍历一边O（N）

（2）使用二分法：我们找到整个数组的中间位置，将它与需要寻找的指定数字进行比较，若中间数字比目标数字小，则我们可以确定该数字在整个数组的右边，再对右半边数组进行二分，找到中间的数字比较，继续二分，直到找到该数字。

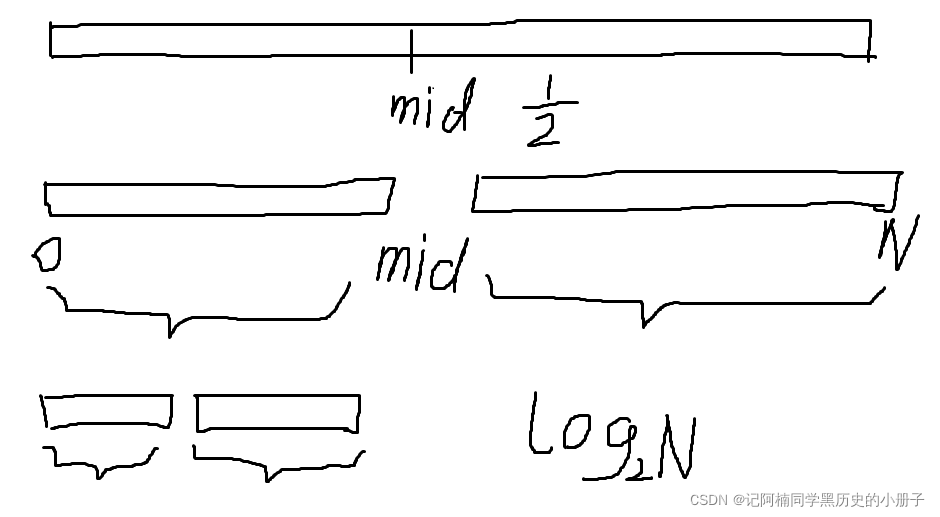
因为每次都是对剩下部分的 二分之一进行一个比较的处理，所以得到时间复杂度为O（logN）

第二个事例

• 在一个有序数组里面，找到大于等于（<=）某个数的最左侧的位置。

 

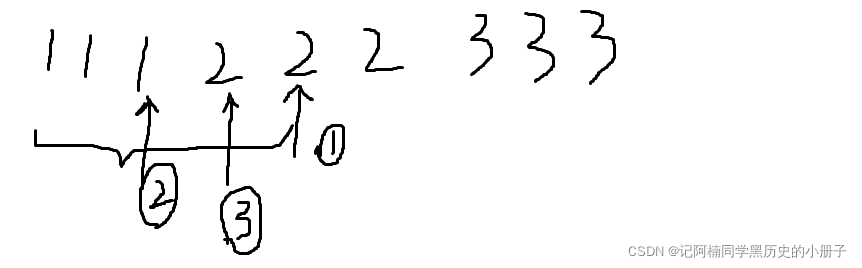
 比如上面这个有序数组，我们目标找到小于等于2的最左侧的那个数字，首先进行二分，找到中间的2，等于目标数字（但是不确定它是不是最左侧的），我们选择左半边的数组再进行二分，得到1，小于目标数字，说明目标数字在它的右边，我们以它为左边边界，前一个2作为右边边界，继续进行二分，等于2，然后发现它的左边只有1个1，得出我们要找的目标数字。（ps：它与前一个事例的一个重要区别，它必须二分到底，才得到我们的结果）

第三个事例

（二分法并非只有在有序数组里面使用，无序数组中同样适用）

• 在一个无序数组中，需要找到一个局部最小的数。（局部最小，就是一个数字比它两边都小，比如[312]，该数组中“1”就是局部最小，同样两头的数[132],该数组中“1”和“2”都是局部最小）

我们在遇到题目时，首先一定要先看它的特性，无论是否是有序。

首先查看两头的数字是不是局部最小，如果是，则可以直接返回，若不是，我们进行二分，找到中间数字查看是否是局部最小，若不是则它大于两边的数字，那么，无论是左边还是右边都一定存在一个局部最小，看下图参考理解。

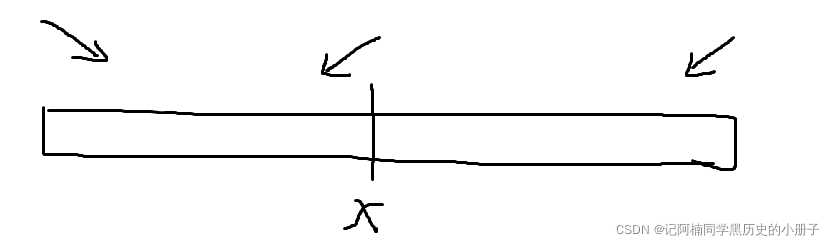
 它们在旁边一定有一个向下降的势，两头都是下降那么中间一定有一个局部最小。