文章详细解析了LeetCode中的三数之和问题的多种解法，包括排序加暴力枚举、双指针配合去重操作。同时，介绍了四数之和的解题思路，同样涉及到排序、双指针以及防止重复和遗漏的处理。并提供了最接近的三数之和问题的解决方案，利用数组有序性和双指针优化算法。
一)三数之和:
如果数组已经有序了，请先想到两个算法，双指针和二分查找
排序+暴力查找+hashSet去重
1)这个题的暴力枚举是很麻烦的，先固定三个数，将所有的三元组枚举出来，在数组无序的情况下还需要进行去重操作；
i!=j!=k，还有上面的[-1，0，1]和[0，1，-1]虽然下标都不相同，但是里面的元素都是相同的，所以说最终我们还是需要进行考虑一种情况即可，这种的去重操作一般来说就比较麻烦
2)针对于暴力破解这个方法来说，最终的去重操作是非常麻烦的，其中一个思路就是针对里面result中的的每一个元素List<Integer>进行排序，然后使用HashSet来进行去重操作
就是将最终的每一个三元组进行排序，然后进行去重；
2.1)使用Stream流的方式实现去重
2.2)使用HashSet集合的方式实现去重
class Solution { public List<List<Integer>> threeSum(int[] array) { //1.先进行对数组进行排序,这样排序完成之后得到的数对的顺序都是相同的 Arrays.sort(array); List<List<Integer>> result=new ArrayList<>(); for(int i=0;i<array.length-2;i++){ for(int j=i+1;j<array.length-1;j++){ for(int k=j+1;k<array.length;k++){ if(array[i]+array[j]+array[k]==0){ List<Integer> list=new ArrayList<>(); list.add(array[i]); list.add(array[j]); list.add(array[k]); result.add(list); } } } } //2.使用JAVA中的hashSet来进行去重 HashSet<List<Integer>> set=new HashSet<>(); for(List<Integer> list:result){ set.add(list); } //3.清空result中的元素,重新将HashSet中的元素存放到result中 result.clear(); for(List<Integer> list:set){ result.add(list); } return result; } }
思路2:将整个数组排序+暴力枚举+去重操作，那么最终的每一个三元组就是有序的，于是就可以使用HashSet进行去重了，将整个数组排序就是为了避免计算出List<Integer>的时候还要讲里面的元素进行排序，然后再来使用HashSet来进行去重操作
[-1，1，0] [-1，-1，2] [-1，1，0]
思路3:双指针+手动去重操作
1)算法原理，核心思路:首先进行排序+固定一个数top+在该数后面的区间内，利用双指针算法快速找到两个数的和等于-a
2)保证不漏操作:
解决方法:当我们的left指针和right指针所指向的数的和等于target值的时候，此时我们应该继续从[left，right]区间内来查询我们最终想要进行寻找的数字，此时应该让left++，right--
当我们找到一种结果之后，不要停止left和right指针的移动，应该缩小[left，right]区间，继续在缩小的区间进行寻找
3)去重操作:要想真正的实现去重操作:
3.1)在指定的区间之内找到一种结果之后，left指针和right指针要跳过重复元素
3.2)当使用完一次双指针算法以后，top也许要跳过重复元素，防止程序继续执行双指针算法再次查找值是-top的两数之和；
4)代码优化:
4.1)常数级别的优化:在这里面还是有一个小小的优化的:假设如今target=0，top元素已经走到了10这个元素位置，但是此时要在10的后面找到一个和是-10来和10进行相加得到0，但是因为数组此时是有序的，一旦top定位到了一个正数的元素，那么在后面永远无法匹配到一个数和当前top下标位置的元素相加之和等于0，所以top指向的下标的元素要大于等于0；
4.2)如果发现数组的元素小于3个，那么直接返回null
class Solution { public List<List<Integer>> threeSum(int[] array) { List<List<Integer>> result=new ArrayList<>(); HashSet<List<Integer>> set=new HashSet<>(); if(array==null||array.length==0){ return null; } if(array.length<3){ return null; } Arrays.sort(array); for(int top=array.length-1;top>=2;top--){ int right=top-1; int left=0; int target=-array[top]; while(left<right){ if(array[left]+array[right]>target){ right--; }else if(array[left]+array[right]<target){ left++; }else{ List<Integer> list=new ArrayList<>(); list.add(array[left]); list.add(array[right]); list.add(array[top]); result.add(list); //以前是找到相同的元素直接进行跳过了,现在直接采取缩小区间的方式进行保证不遗漏 left++; right--; } } } List<List<Integer>> newList = result.stream().distinct().collect(Collectors.toList()); return newList; } }class Solution { public List<List<Integer>> threeSum(int[] array) { //1.存放返回值的List<Integer>的元素 List<List<Integer>> result=new ArrayList<>(); if(array==null||array.length==0){ return null; } if(array.length<3){ return null; } //2.对数组进行排序,只有先进行排序之后,在使用双指针算法进行解决问题 //一旦看到了排序,首先想到的算法是双指针+二分查找 Arrays.sort(array); for(int top=array.length-1;top>=2&&array[top]>=0;top--){ //3.进行去重操作,防止进行重复的双指针算法进行查找以前曾经相同的target值 if(top+1<array.length&&array[top]==array[top+1]){ continue; } //4.使用双指针算法进行解题 int right=top-1; int left=0; int target=-array[top]; while(left<right){ if(array[left]+array[right]>target){ right--; }else if(array[left]+array[right]<target){ left++; }else{ List<Integer> list=new ArrayList<>(); list.add(array[left]); list.add(array[right]); list.add(array[top]); result.add(list); int leftdata=array[left]; int rightdata=array[right]; //5.此处还要防止数组越界,所以让left指针进行++操作去除掉重复元素,right指针进行 //--操作去除掉重复元素 while(left<right&&array[left]==leftdata){ left++;//防止数字越界 } while(left<right&&array[right]==rightdata){ right--; } } } } return result; } }最推荐的写法:class Solution { public List<List<Integer>> threeSum(int[] nums) { List<List<Integer>> ret=new ArrayList<>(); Arrays.sort(nums); for(int top=nums.length-1;top>=2;){ int left=0,right=top-1; int target=-nums[top]; while(left<right){ if(nums[left]+nums[right]>target){ right--; }else if(nums[left]+nums[right]==target){ List<Integer> list=new ArrayList<>(); list.add(nums[left]); list.add(nums[right]); list.add(nums[top]); ret.add(list); int leftData=nums[left]; int rightData=nums[right]; while(left<right&&nums[left]==leftData) left++;//不重 while(left<right&&nums[right]==rightData) right--;//不重 //找到一种结果之后不要停,继续缩小两个指针的区间,继续寻找 }else{ left++; } } int topData=nums[top]; while(top>=2&&topData==nums[top]) top--;//不重 } return ret; } }时间复杂度O(N^2)
二)四数之和:
一)暴力解法:数组排序+暴力枚举(四循环)+HashSet去重
在某一次选择中不能选择相同的数(i!=j!=k!=x)
二)双指针:数组排序+双指针，我们的三树之和是固定一个数，在后面的区间中找到两个数之和等于目标值target，那么我们四数之和的思想也很简单
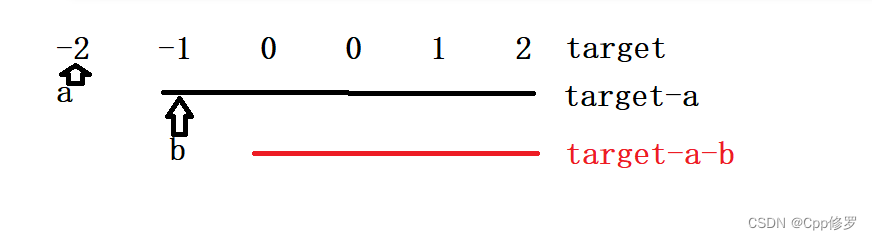
2.1)依次固定一个数a
2.2)在后面的区间1中利用三数之和找到三个数，是他们这些数的和等于target-a即可
2.3)在后面的这个区间1中，固定一个数b，利用双指针找到两个数，使这两个数的和等于target-a-b
所以我们要需要使用两层for循环来依次枚举两个数，然后从剩下的区间中使用双指针算法
不重:不能选择相同的数
1)当我们计算出结果之后，left如果遇到相同的数就一直进行++操作，right指针如果遇到相同的数就一直进行--操作；
2)当我们b遇到重复的数的时候需要跳过相同的数，同理，a遇到相同的数的时候也是需要跳过相同的数
不漏:当我们的left指针和right指针在遇到相同的数的时候，直接进行缩小区间，继续进行寻找
class Solution { public List<List<Integer>> fourSum(int[] array, int target) { List<List<Integer>> result=new ArrayList<>(); if(array==null||array.length==0){ return null; } Arrays.sort(array); for(int top1=0;top1<array.length-3;){//先固定一个数a for(int top2=top1+1;top2<array.length-2;){//在固定一个数b //使用双指针算法 long info=((long)target-array[top1]-array[top2]); int left=top2+1; int right=array.length-1; while(left<right){ if(array[left]+array[right]<info){ left++; }else if(array[left]+array[right]>info){ right--; }else{ List<Integer> list=new ArrayList<>(); list.add(array[left]); list.add(array[right]); list.add(array[top1]); list.add(array[top2]); result.add(list); int leftdata=array[left]; int rightdata=array[right]; //保证不漏,继续缩小区间 //去重,还需要保证不能越界 while(left<right&&array[left]==leftdata){ left++; } while(left<right&&array[right]==rightdata){ right--; } } } //在每一次top2元素固定完成一次双指针之后,继续判断下一个元素是否和当前循环中判断的元素是否相等,如果相等就执行++操作 top2++; while(top2<array.length&&array[top2]==array[top2-1]){ top2++; } } //在每一次top1元素固定完成之后,判断下一个元素是否等于当前元素 top1++; while(top1<array.length&&array[top1]==array[top1-1]){ top1++; } } return result; } }
class Solution { public List<List<Integer>> fourSum(int[] array, int target) { List<List<Integer>> result=new ArrayList<>(); Arrays.sort(array); for(int i=0;i<=array.length-4;i++){ if(i>=1&&array[i]==array[i-1]) continue; for(int j=i+1;j<=array.length-3;j++){ if(j>i+1&&array[j]==array[j-1]) continue; long targetData=((long)target-array[i]-array[j]); int left=j+1; int right=array.length-1; while(left<right){ if(array[left]+array[right]>targetData) right--; else if(array[left]+array[right]<targetData) left++; else{ List<Integer> tempList=new ArrayList<>(); tempList.add(array[i]); tempList.add(array[j]); tempList.add(array[left]); tempList.add(array[right]); result.add(tempList); int leftData=array[left]; int rightData=array[right]; while(left<right&&array[left]==leftData) left++; while(left<right&&array[right]==rightData) right--; } } } } return result; } }
三)最接近的三数之和:
class Solution { public int threeSumClosest(int[] nums, int target) { //1.先将整个数组进行排序 Arrays.sort(nums); if(nums.length<3) return -1; int ans=nums[0]+nums[1]+nums[2]; for(int i=0;i<=nums.length-3;i++){ int top=nums[i]; int left=i+1; int right=nums.length-1; while(left<right){ int sum=top+nums[left]+nums[right]; if(Math.abs(target-sum)<Math.abs(target-ans)){ ans=sum; } if(sum>target) right--;//让距离变得更小 else if(sum<target) left++;//让距离变得更小 else return ans; } } return ans; } }
要尤其注意上面的划红线的这种写法
单调性+数组有序+双指针
四)长度最小的子数组
第一种解法:暴力枚举时间复杂度是O(N^2)
1)可以将这个数组中的所有子数组进行枚举一遍，然后求出它们的和再和目标值进行比较
2)首先让i固定到一个位置，j从i开始走，sum=sum+array[j]不断进行累加，每次累加到一个元素的时候进行判断，如果这个和大于等于target，计算他们元素之间的个数
3)注意，j此时走到这里就可以了，j不需要再向后走了，因为j向后走进行相加的和一定是大于target的况且right-left的值也是在不断增大的，也就是说它们之间的元素个数是在不断增大的，而我们题目中要找的是最小的元素个数，虽然j向后走元素之和满足要求，但是元素个数却是在不断增大的；
4)虽然满足元素和大于target，但是j向后走所以没必要，直接退出循环就可以了，重新再让left进行向后++，前提是后面的数都是正数
5)这里成功利用了单调性，规避了很多没有必要的枚举行为，因为都是正数，所以加的数越多，和就会越大，sum:以i为左区间，right为动态右区间的子数组的和
class Solution { public int minSubArrayLen(int target, int[] array) { int value=Integer.MAX_VALUE; int max=-1; for(int i=0;i<array.length;i++){ int sum=0; for(int j=i;j<array.length;j++){ sum=sum+array[j]; if(sum>=target){ value=Math.min(value,j-i+1) ; break; } } } return value==Integer.MAX_VALUE?0:value; } }
第二种解法:同向双指针+滑动窗口
利用单调性，采用同向双指针来优化，因为从上面暴力解法得出的结论来看，left指针和right指针都是在向右移动的，right不会回退，所以滑动窗口先看暴力解法
1)单调性
2)双指针不回退
3)在同向双指针区间内维护区间里面的一部分信息
同向双指针也被称之为滑动窗口，定义的left指针和right指针都在向一个方向走，滑动窗口算法是在两个指针都不进行回退的情况下，在滑动窗口中，我们所进行维护的就是left到right之间的信息，在这个题中，所进行维护的就是left到right区间里面的和，在left和right移动的过程中，十分类似于窗口在数组中进行移动，这就是所谓的滑动窗口；
什么时候用滑动窗口?暴力枚举发现双指针同向移动，利用单调性
出完窗口的时候为什么还要继续进行判断呢？
为什么出完窗口之后需要继续进行判断，因为一次出窗口之后只是出了一个元素，此时区间元素的和可能还是大于等于target的，而这个区间的长度离我们最终的目标结果又近了一步，所以说我们出完窗口之后还是要继续进行判断的这时一个while循环是需要不断进行判断
class Solution { public int minSubArrayLen(int target, int[] array) { int left=0; int right=0; int len=Integer.MAX_VALUE; int sum=0; while(right<array.length){ while(right<array.length){ //1.先将从left到right下内的值全部进行相加,一定是先将sum求和,在移动right指针 sum=sum+array[right]; //2.如果sum的值已经大于了target的值,那么直接可以跳出循环,right指针不需要再次向后移动 if(sum>=target){ break; } right++; } //3.代码走到这里说明sum的值已经大于等于target了,此处需要先更新len的值 while(sum>=target){ //先进行更新len的值,再进行更新left指针的值,只要sum的值大于等于target,left指针就一直向右进行移动 if(sum>=target){ len=len>right-left+1?right-left+1:len; } //4.更新完值之后,还要将left指针向后进行移动一步 //此处right指针不需要向后进行移动 left++; sum=sum-array[left-1]; } //5.只有当sum的值小于target的时候,right指针才会向后移动 right++; } if(len==Integer.MAX_VALUE){ return 0; } return len; } }1)先进行定义指针:left=0，right=0，维护的窗口信息就是sum，左区间到右区间内所有的数的和；
2)进入到窗口:如果[left，right]区间之内的和小于target，那么就移动right指针，因为你此时移动left指针也没有什么卵用了，就算你移动left指针，最后移动完成之后[left，right]之间的和会变得越来越小
3)判断:
4)出窗口:如果[left,right]区间内的和大于target，也就是有可能说left在向右移动之后，left和right的和仍然是大于target的值的，此时符合题意，但是len的值已经变小了，此时距离满足题意就更进了一步，所以你此时移动完left指针之后要继续进行判断left和right区间内的数是否大于target的值，如果还是sum大于等于target，更新len的值，继续移动left指针，如果移动完成之后发现[left，right]之间的值小于target，此时可以再次进行移动right指针了
5)滑动窗口的正确性:因为本题数组是具有单调性的，[left，right]区间内的和大于等于target，虽然right没有继续向后移动，但是其实向后移动也没什么用，即使枚举，也是瞎枚举，一定不符合最终的结果，这就叫做使用单调性，规避了很多没有必要的枚举，虽然没有进行全部枚举出来，但是在这个策略中已经判断过了，从而进行筛选，根据单调性得知后面的情况一定不是最终枚举的结果，此时就应该让left指针向后进行移动
6)虽然代码中有两层循环，但是实际上每一次只会让left指针或者是right指针向后移动一格，直到right指针移动到最后一个位置，所以移动次数最多也就是2N，时间复杂度是O(N)；
class Solution { public int minSubArrayLen(int target, int[] array) { int n=array.length-1,sum=0,len=Integer.MAX_VALUE; for(int left=0,right=0;right<array.length;right++){ //判断当前的值是否小于target,小于的话就让right++,增大窗口内和的值 sum=sum+array[right];//进窗口 while(sum>=target){ //判断当前窗口内和的值是否大于target,如果是就将left++,进行出窗口的操作,减少窗口内和的值 len=Math.min(len,right-left+1); sum=sum-array[left]; left++; } } if(len==Integer.MAX_VALUE) return 0; return len; } }
推荐写法:窗口中维护的信息就是sum和
因为我们要求的是大于等于taregt的长度最小的子数组，所以要在sum大于等于target的时候的那一刻统计结果，然后再次移动指针left，进行出窗口
扫一扫
6011
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
