一.数字太大溢出与取模
假设x是一个连整型long long都装不下的整数,那么x在存储区将会由于溢出表示为一个负数,那么想不影响计算,可以使用(x%mod+mod)%mod(mod为题目要求取余的数字)来解决。详情可看例题:
例一
题目描述
吃葡萄的叮当猫今天遇到了一个数学问题!
你能帮她算出来 f(n) 的值吗
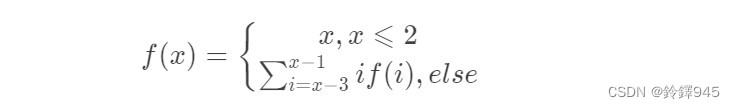
答案可能很大,请你输出 f(n)mod1e9+7 的值
输入格式
一行一个整数 n
输出格式
f(n)mod1e9+7 的值,每个一行
输入输出样例
输入
3
4
输出
5
20
对于 20% 的数据,1⩽n⩽100
对于 50% 的数据,1⩽n⩽1000
对于 100% 的数据,1⩽n⩽2×10^5
注意:本题可能存在多组输入数据,请使用while(scanf() != EOF)的语句结构来控制输入
本题逻辑较简单,主要是注意取余时的技巧,以及在已经给出100%的数据范围时,可以提前将数据全部算好存在数组中,省得对于每一个n都要多次计算。
代码在这
#include<stdio.h>
long long f[200001];
int mod=1000000000+7;
int main()
{
f[0]=0;
f[1]=1;
f[2]=2;
for(int i=3;i<=200000;i++)
{
for(int j=i-3;j<=i-1;j++)
{
f[i]=(f[i]+(j*f[j]%mod+mod)%mod)%mod;
}
}
int n=0;
while(scanf("%d",&n)!=EOF)
{
printf("%lld\n",f[n]);
}
return 0;
}二.分冶算法典例
例二
题目描述
FFT 在计算机领域中可以通过递归来实现,但是使用递归将占用大量计算机内存,为了简化流程,通常将 FFT 展开成迭代形式进行计算,这其中 蝴蝶变换(bit-reversal permutation)蝴蝶变换(bit−reversal permutation) 起到了相当重要的作用。
蝴蝶变换蝴蝶变换 本质上是一种分治算法,其算法如下:
1.首先判断初始序列长度是否满足 2 的整数次幂,如果不满足,在序列尾补 0 直至序列长度为 2 的整数次幂,否则序列不变
2.对新序列,按照元素位置的奇偶来分成两组
3.对划分成的两组序列,根据在新的序列中的位置,按照奇偶性进行划分,每一个序列又划分成新的两组序列
4.当一个序列只剩下一个元素时,划分结束
一个蝴蝶变换的实例:
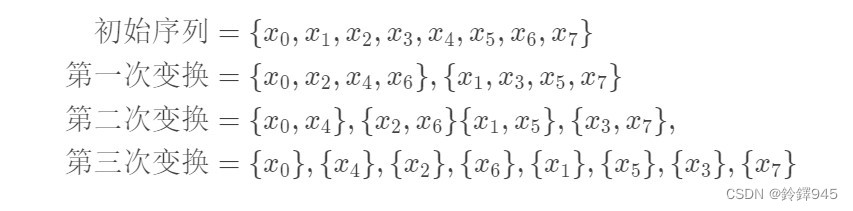
输入格式
第一行一个正整数 n
接下来一行输入 n 个整数 a[i]
输出格式
蝴蝶变换的结果序列
输入
8 0 1 2 3 4 5 6 7
输出
0 4 2 6 1 5 3 7
对于 10% 的数据,1⩽n⩽10^3
对于 20% 的数据,1⩽n⩽10^4
对于 30% 的数据,1⩽n⩽10^5
对于 100% 的数据,1⩽n⩽10^6
对于 100% 的数据,0⩽a[i]⩽10^9
思路
这道题首先要将序列补成2的整数次幂,所以也是要进行预处理,将大于1而且小于等于超过10^9的第一个2的整数次幂全部存到数组中,方便补零;
然后就到分治的函数,可以发现每一次操作都是把一个数列分成两个一奇一偶数列,那么我们用函数递归就可以搞定,按部就班。
代码贴
#include<iostream>
#include<cmath>
using namespace std;
int fenzhi(int a[], int x)
{
if(x==2)
{
cout<<a[0]<<" "<<a[1]<<" ";
return 0;
}
//a1为奇数列,a2为偶数列
int*a1=new int[x/2];
int*a2=new int[x/2];
int t1=-1,t2=-1;
for(int i=0;i<x;i++)
{
if(i%2==0)
{
a1[++t1]=a[i];
}
else
{
a2[++t2]=a[i];
}
}
//将他们分别再次调用去执行相同操作
fenzhi(a1,x/2);
fenzhi(a2,x/2);
}
int main()
{
//将可能使用到的二的次幂全部存入
int two[21]={1,2,4,8,16,32,64,128,256,512,1024,2048,4096,8192,16384,32768,
65536,131072,262144,524288,1048576};
int n=0;
cin>>n;
int*temp=new int[n];
for(int i=0;i<n;i++)
{
cin>>temp[i];
}
if(n==1)
{
cout<<temp[0]<<endl;
}
else if(n==2)
{
cout<<temp[0]<<" "<<temp[1]<<endl;
}
else
{
int m=0;
for(int i=0;i<=20;i++)
{
if(n==two[i])
{
m=n;
break;
}
else if(n<two[i])
{
m=two[i];
break;
}
}
int*a=new int[m];
for(int i=0;i<m;i++)
{
if(i<n)
{
a[i]=temp[i];
}
else
{
a[i]=0;
}
}
fenzhi(a,m);
}
return 0;
}三.区间加法不再TLE
这种题思路就是在每个要进行加法操作的区间在两端将变化量表示出来,每次操作只标识出变化量,最后再做一次前缀和就能出来,而不用每次都对要操作的区间进行一个一个的加法。
概括:假设有一个a数列,要对l到r区间内的所有数加上x,那么只要a[l]+=x,a[r+1]-=x,最后再做一次前缀和就好了,例如a=[1,2,3,4,5],那么再设一个数列为t=[0,0,0,0,0,0],(初始操作数列要为零,且要多一位在r为边界时去给r+1使用),对a[1]到a[4]区间进行加2操作,t[1]+=2,t[r+1]-=2;即t变为[0,2,0,0,0,-2],做前缀和后t变为[0,2,2,2,2,0],将最后一位记数位去掉,a=a+t(各自对应相加),就完成了一次加法操作,多次加法操作每次只要进行a[l]和a[r+1]操作,最后做一次前缀和加法就好了。
例三
题目描述
这一天 uwu 穿越来到了提瓦特大陆!
这片提瓦特大陆上有 n 种怪物,而 uwu 作为一个刚刚穿越而来的旅行者,他的等级只有可怜的 1 级!
为了能在提瓦特大陆上遨游, uwu 决定努力提升自己的等级!
已知 uwu 在 11 级时,每一次攻击能够对这 n 种怪物中的第 i 种造成 a[i] 的伤害
uwu每升一级,它能够对怪物的伤害都将得到提升!
可是提瓦特大陆存在等级限制, uwu只能够提升 m 次自己的等级
每当提升 1 级时, uwu 能够对第 l 至第 r 种怪物提升 k 点伤害!
注意, uwu 每提升一级,提升的伤害值 k 以及受到伤害提升的怪物的区间 [l,r] 可能会有所不同
现在,请你帮助 uwu ,计算出提升了 m 次等级后, uwu 能对这 n 种怪物一次攻击所造成的的伤害值
输入格式
第一行两个正整数 n,m ,表示有 n 种怪物和 m 次等级提升
第二行 n 个正整数,为 uwu 等级为 1 时对第i(1⩽i⩽n) 种怪物一次攻击造成的的伤害值
接下来 m 行,每行三个整数 l,r,k ,含义为对 [l,r] 范围内的怪物造成的伤害提升 k
输出格式
uwu 提升了 m 次等级之后对这 n 种怪物造成的伤害值
输入输出样例
输入
3 2 2 4 7 1 2 3 2 3 4
输出
5 11 11
代码贴
#include<iostream>
using namespace std;
int main()
{
int m=0,n=0;
cin>>n>>m;
int*w=new int[n];
for(int i=0;i<n;i++)
{
cin>>w[i];
}
int*x=new int[n+1];
for(int i=0;i<=n;i++)
{
x[i]=0;
}
int l=0,r=0,k=0;
for(int i=1;i<=m;i++)
{
cin>>l>>r>>k;
l-=1;
r-=1;
x[l]+=k;
x[r+1]-=k;
}
for(int i=1;i<=n;i++)
{
x[i]+=x[i-1];
}
for(int i=0;i<n;i++)
{
cout<<w[i]+x[i]<<" ";
}
return 0;
}四.字典序
例四
输出1到n的字典序排列,一行代码(指核心代码)
next_permutation(a,a+n);
将数组a到a+n的数进行字典序排列
代码贴这
#include<iostream> #include<algorithm> using namespace std; int main() { int a[6]={6,5,4,3,2,1}; int n=6,j=720; //提前算好字典序一共几种可能n*(n-1)*......*2*1 for(int i=1;i<=j;i++) { next_permutation(a,a+n); for(int k=0;k<n;k++) cout<<" "<<a[k]; cout<<endl; } return 0; }
五.全排列(与字典序一样,但是用正常解法,剪枝加回溯)
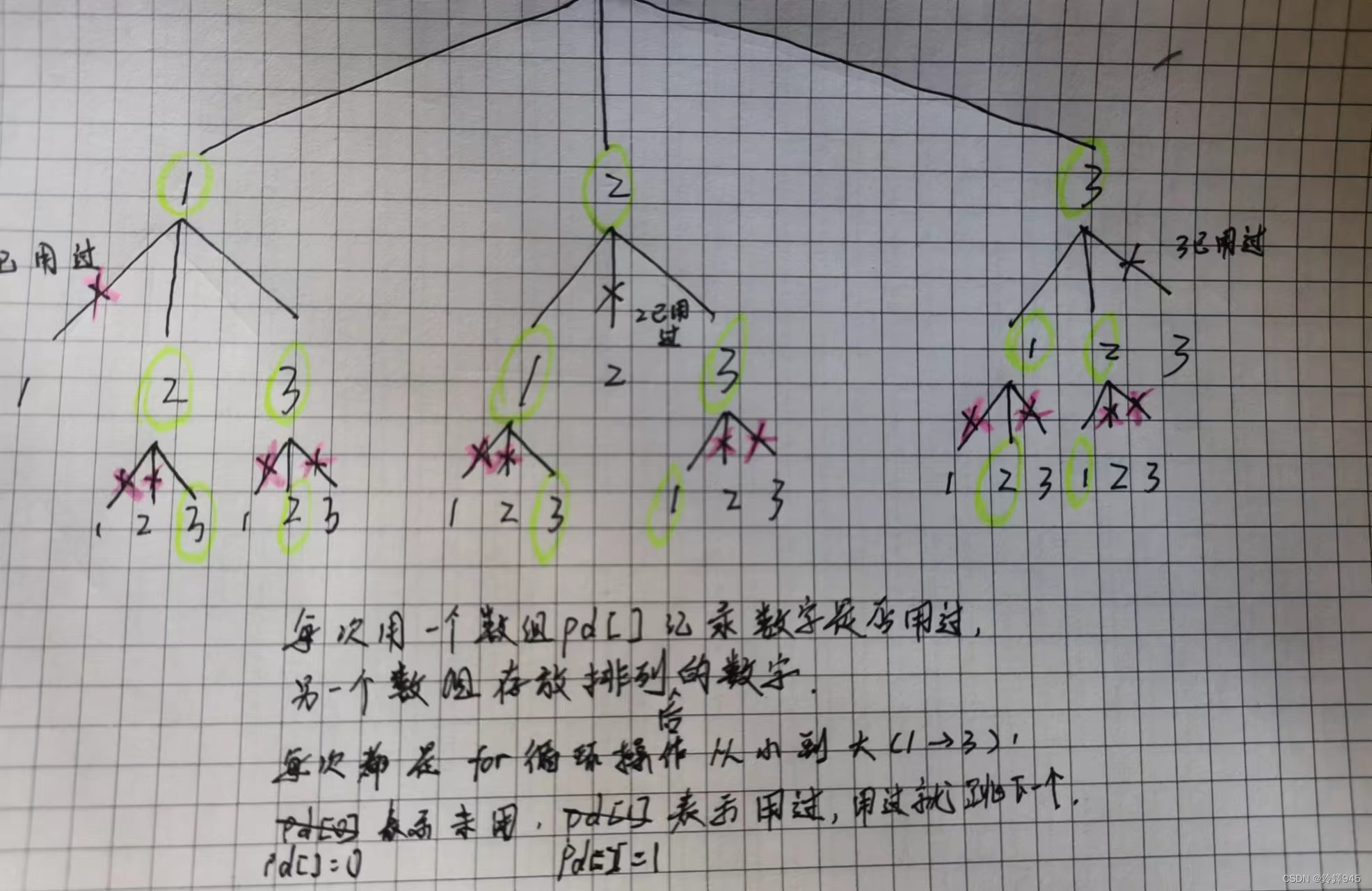
题目链接
代码贴这
#include<iostream>
using namespace std;
int n,pd[100],used[100];
void fn(int x)
{
if(x>n)
{
for(int i=1;i<=n;i++)
{
cout<<used[i]<<" ";
}
cout<<endl;
return ;
}
for(int i=1;i<=n;i++)
{
if(!pd[i])
{
pd[i]=1;
used[x]=i;
fn(x+1);
pd[i]=0;
}
}
}
int main()
{
cin>>n;
fn(1);
return 0;
}六.素数快速判定
求某范围内的质数方法有很多种,详细的可以看这位博主写的,
求质数(素数)算法,及算法优化_# Never Give up &的博客-优快云博客_找质数的公式
我采用的是第五种较快的算法。然后在求出所有质数后,还要找出可表示的加数的质数中最小的质数,所以我们在遍历每一个加数去求它的质数时,直接从最小的质数开始找起,那么我们刚刚已经求得2~10000内所有质数,但它们是乱序的,那么推荐大家用C++自带的set容器 ,这道题可以应用到set容器的两个特性,1:set容器里的元素不重复而且是有序排列的,默认降序;2:set容器里的元素可以用find()去访问是否存在,不用遍历,减少了我们在判断一个加数是否是质数时的时间复杂度。
下面是求1~1000000的所有质数
代码贴
#include<iostream>
#include<stdio.h>
#include<set>
int a[1000000]={0};
using namespace std;
int main()
{
set<int> prime;
for (int i = 2; i < 1000000; i++)
{
if (!a[i])
{
prime.insert(i);
for (int j = i * 2; j < 1000000; j += i)
{
a[j] = 1;
}
}
}
for(set<int>::iterator it=prime.begin();it!=prime.end();it++)
{
cout<<(*it)<<" "<<endl;
}
return 0;
}不足之处多多指教☺



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








