粒子群、遗传算法以及模拟退火算法

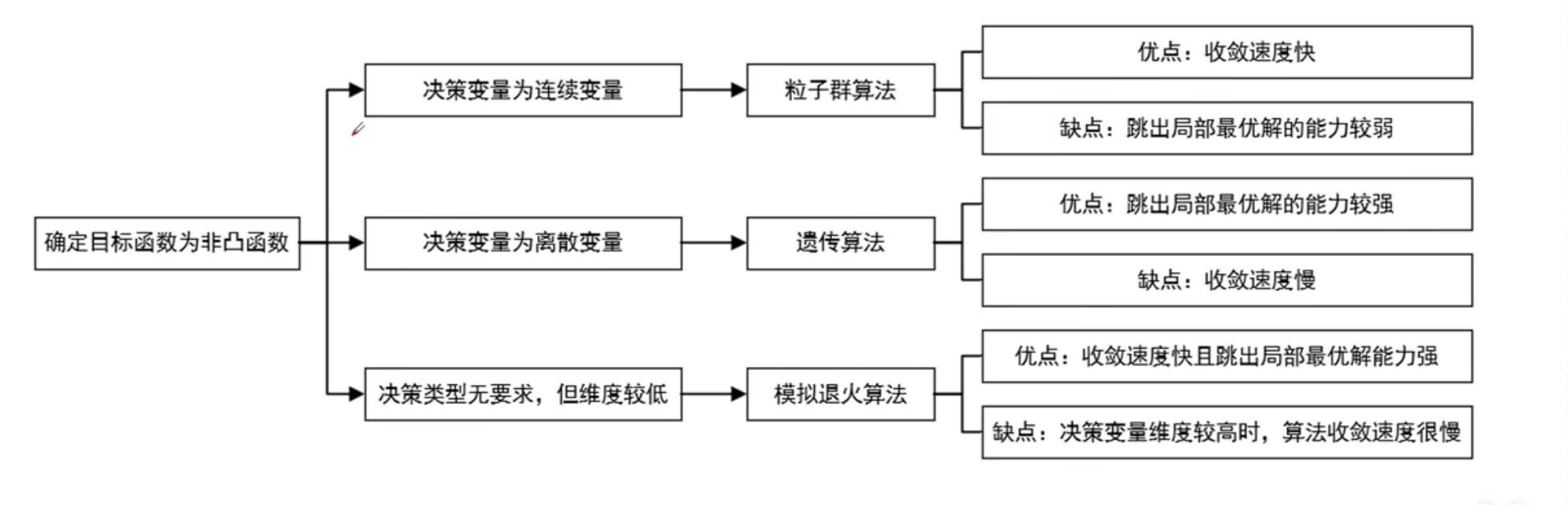
一、遗传算法优化

1.优化

2.概念

1.种群：在解空间中设置许多个个体组成一个群体，也即多个解

2.个体：个体是可能潜在的解空间的解（最优解，次优解或者局部最优解）

3.染色体：也即个体

4.基因：解里面的组成单元（x1,x2,x3,x4,x5）x1到x5称为基因，合在一起称为染色体。

5.适应度（fitness）：评价个体好坏的指标

如下表所示

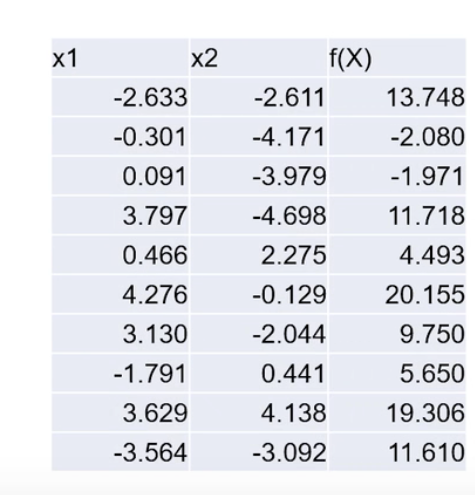
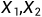称为基因，f(X)称为性状，所有的行称为种群

3.遗传算法的基本操作

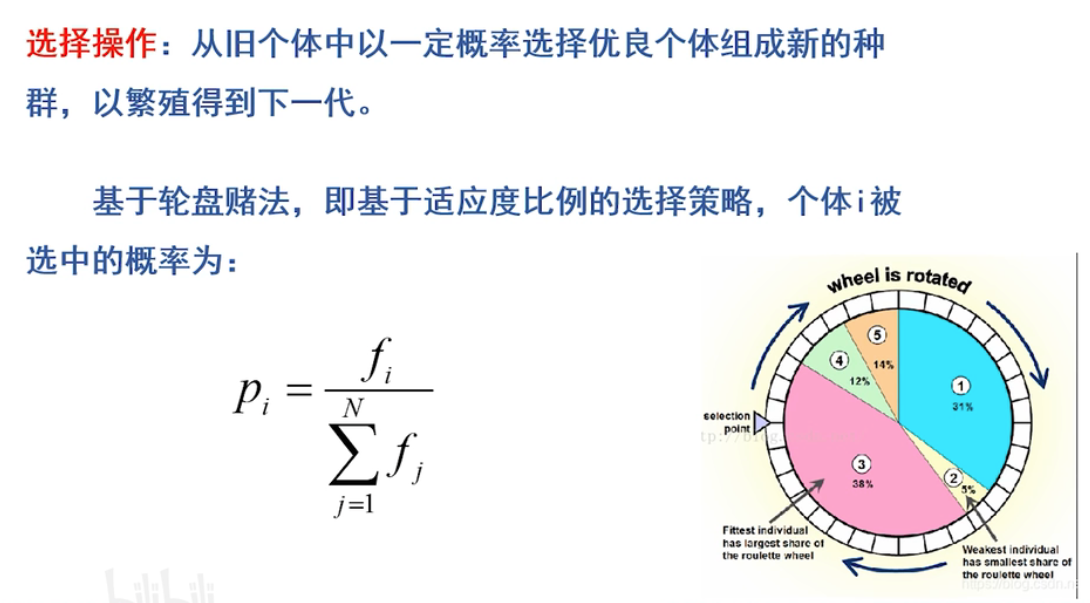
(1).选择操作

从当前群体中选出优良的个体，是他们有机会作为父代为下一代繁衍子孙。选择适应度比较高的个体进入下一代，但并不是适应度高的个体会百分之百的进入下一代。（轮盘赌法）

(2).交叉操作

将群体中的各个个体随机搭配成对，对每一个个体，以交叉概率交换它们之间的部分染色体。

(3).变异操作

对种群的每一个个体，以变异的概率改变某一个或多个基因座上的基因值为其它的等位基因。变异发生概率很低，变异为新个体的产生提供了机会。

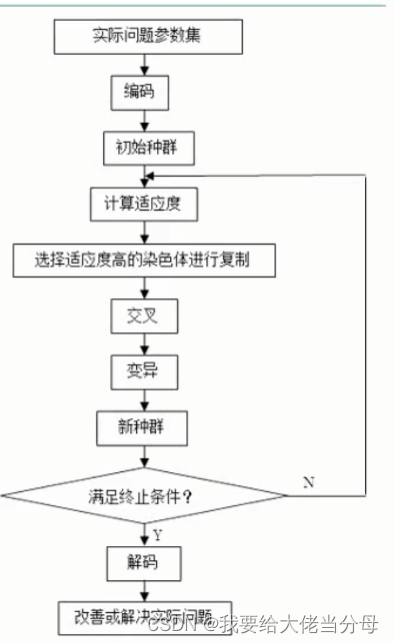
4.遗传算法的基本步骤

1）编码：将解空间的解数据表示成遗传空间的基因串的结构。

2）初始群体生成：随机产生N个初始串结构数据，每个串结构数据称为一个个个体，N个个体构成了一个群体。GA以这N个串结构数据作为初始点开始进化。

3）适应度评估：使用工具箱中的适应度函数

4）选择：选择的目的是从当前群体中选出优良个体，适应性强的个体为下一代贡献一个或多个后代概率大。

5）交叉：产生新的个体，保留父辈个体的一些特性

6）变异: 在群体中随机选择一个个体，对于选中的个体以一定的概率随机地改变串结构数据中某个串地值。通常发生概率很小。

 5.遗传算法的使用

我们使用的是gaot包

（1）initializega

该函数用于创建一个由随机数构成的矩阵，其中矩阵的行数等于种群大小 populationSize，而列数等于变量边界矩阵的行数加 1（多出的 1 列用于存储 f(x) 值，即适应度函数值，该值是通过应用 evalFN 计算得到的）。在遗传算法中，这个函数可以用来生成初始种群，如果用户没有提供种群的话。

• pop：是一个包含初始种群个体的矩阵。每个个体是一个由优化变量值组成的向量，还包括一个额外的列用于存储适应度函数值 f(x)。

• populationSize：种群大小，即需要生成多少个个体。

• variableBounds：一个矩阵，其中包含了每个优化变量的边界值。例如，对于每个变量，边界用行表示，包含两列：第一列是变量的上界，第二列是变量的下界。用这些边界值来限制随机生成的个体的取值范围。

• evalFN：评估函数，通常是用于评估个体适应度的 .m 文件的名称。

• evalOps：传递给评估函数的任何选项，默认为空数组 []。

• options：initialize 函数的选项，例如 [type prec]，其中 type 是 epsilon 值，第二个选项是 1 表示浮点数，0 表示二进制数，prec 是变量的精度，默认为 [1e-6 1]。

该函数的目的是在不提供初始种群的情况下，生成一个具有随机优化变量值的种群，并计算每个个体的适应度函数值。此种群可作为遗传算法的起始点，并随着算法的进化逐渐优化，以找到或接近最优解。

pop = initializega(populationSize, variableBounds, evalOps, options)

参数	意义
pop	随机生成初始种群
populationSize