考研时间复杂度和空间复杂度的计算看这一篇就够了

目录

一.时间复杂度定义

二.时间复杂度的计算方法

三.例题 

3.1 折半查找时间复杂度

3.2 递归累乘的时间复杂度 

3.3：递归累加 

3.4 斐波拉切数列 

四.空间复杂度

4.1 空间复杂度是数额外空间。

4.2 计算方法 

4.3 例题

3.3.1 冒泡排序 

3.3.2 开辟数组

3.3.3 递归调用和斐波拉切数列的空间复杂度 

---

一.时间复杂度定义

1.时间复杂度是估计，O（n），最坏情况。

二.时间复杂度的计算方法

1. 常数O（1）

2. 直观的数循环

3.不直观的用思想去做。

三.例题 

3.1 折半查找时间复杂度

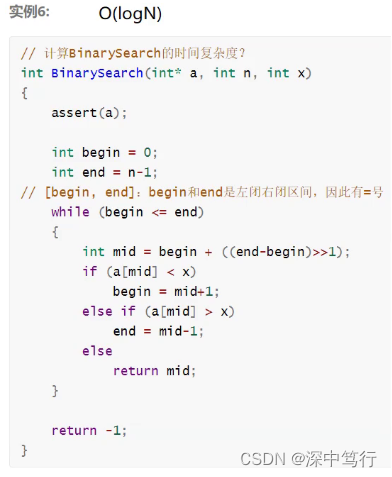
3.2 递归累乘的时间复杂度 

 

累乘n次调用了n次函数,所以时间复杂度为O（n）。

 

 

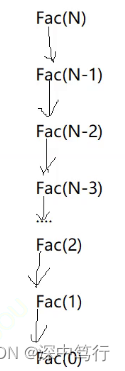
3.3：递归累加 

 

这里N，循环执行N次，调用函数Fac，循环9次，直到循环0次是一个等差数列。 

 

3.4 斐波拉切数列 

 

 

我们会发现这里类似于等比数列求和，可以用错位相减。 所以时间复杂度为O（）

 

四.空间复杂度

4.1 空间复杂度是数额外空间。

空间复杂度不是O（N），就是O（1），除了快排O（log N），二维数组（）

4.2 计算方法 

数自己额外定义的变量，指针，数组等。

4.3 例题

3.3.1 冒泡排序 

 

这里我们定义了 size_t，exchange，i。等虽然定了很多变量但任然是常数，所以空间复杂度为 O（1） 

3.3.2 开辟数组

这里我们发现，我们定义了一个n+1个空间的数组，所以我们额外用了n+1个空间。所以我们时间复杂度为O（n） 

3.3.3 递归调用和斐波拉切数列的空间复杂度 

注意(❁´◡`❁) 

1. 递归的过程不是同时调用的，先让+号左边的递归完，在让+后的递归

2. 时间是累计的，一去不复返。

2. 空间虽然也是累加，但是空间是可以重复利用的。

 

这里用到了函数栈帧的知识。

在Fib(N-1)调用完了之后，就会销毁。但是空间会留下来，给右边的Fib（N-2）使用，所以空间可以重复使用。 Fib1和Fib2调用是一块栈帧的空间。

所以这题空间复杂度是O（N）