可视化B树详细代码实现

本次实验将实现一棵具备完整功能且正常运行的B树，并用dot脚本语言实现B树的可视化，能够根据操作实时进行B树的结构变换。

参考教材：殷人昆老师版 数据结构

代码链接：BTree Visualize

数据结构：B树

此处仅做简介，详细请见教材。B树是一种常用的多路平衡搜索树（也称为多叉树），可以看作平衡二叉树的更为平常的版本，但是拥有m路的B树更加复杂。B树被广泛应用于数据库和文件系统等存储结构中，以支持高效的数据插入、删除和查找操作。B树的特点是每个节点可以存储多个关键码（即key值），并且节点之间的高度尽量保持一致，从根节点到每一个叶子节点的路径长度基本相等，且失败节点均在同一层上，保证了数据的均衡性和快速访问。

B树有如下特性：

1. 每个节点最多有M个子节点（M>=2），即最多有M-1个关键码。通常情况下，M的值很大，可以存储大量的关键字，从而减少树的高度，提高数据访问效率；
2. 根节点至少有两个子节点；
3. 非根节点至少有ceil(M/2)个子节点，即至少有(M-1)/2个关键码；
4. 所有叶子节点位于同一层，即它们具有相同的深度；
5. B树的插入和删除操作都需要进行树的平衡调整，以保持B树的特性。
   在插入操作中，如果插入后导致节点的关键字数超过了M-1个，需要进行节点的分裂，将一部分关键字移到一个新节点中，然后将新节点插入到父节点中。
   
   

在删除操作中，如果删除导致节点的关键字数少于(M-1)/2个，需要进行节点的合并，将相邻的两个节点合并为一个节点，然后将父节点中的关键字删除。

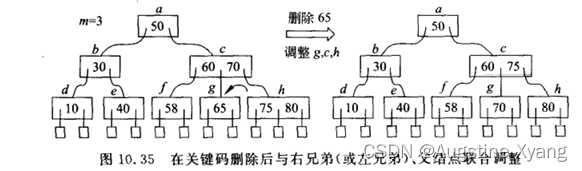
B树的平衡调整过程比较复杂，但它保证了B树各路的高度平衡，从而保证了高效的数据访问速度。B树的应用广泛，特别是在数据库索引和文件系统中，它能够高效地支持大规模数据的存储和查询。

B树代码实现

查找

这是B树的基本功能，search方法会根据关键码在树中搜寻其位置，如果搜寻不到，则会返回该关键码的插入位置

struct ans
{
   
	Bnode* r;   //地址
	int i;    //关键码
	bool tag;  // 0成功，1失败
};

ans BTree::search(const int& x)
{
   
	ans result;
	Bnode* p = root, * q = NULL;//p为扫描指针，q为p的父结点指针
	int i = 0;
	while (p != NULL)
	{
   
		i = 0;
		p->key[(p->num) + 1] = maxValue;
		while (p->key[i + 1] < x)i++;
		if (p->key[i + 1] == x)
		{
   
			result.r = p;
			result.i = i + 1;
			result.tag = 0;
			return result;
		}
		q = p;
		p = p->child[i];    //下移到相应子树

	}
	result.r = q;
	result.i = i;   //记录位置i
	result.tag = 1;
	return result;
}

插入

插入操作会先调用search方法，即可找到该关键码在树中应当插入的位置

bool BTree::insertKey(Bnode* p, const int& x, Bnode* rp)  //用于在p节点中插入一项x
{
   
	int i = p->num;
	while (i > 0 && x < p->key[i])
	{
   
		p->key[i + 1] = p->key[i];//向后移位
		p->child[i + 1] = p->child[i];
		i--;
	}


	p->key[i + 1] = x;   //插入x
	p->child[i + 1] = rp;
	p->num++;

	return true;
}


bool BTree::insert(const int& x)
{
   
	ans pos = search(x);
	if (!pos.tag)
		return false;//x已经存在
	Bnode* p = pos.r;  //p为要插入的地址
	Bnode* q, * t, * rp = NULL;
	int k = x;
	int j = pos