1. 问题背景
表格数据具有以下的特殊性:(1)表格数据包含表示连续、分类和有序值等多个特征,其中值可以是独立的,也可以是相关的。(2)表格数据中列的顺序可以是任意的,没有固定的位置信息
由于表格数据的特殊性,表格模型必须处理来自多个离散和连续分布的特征,并且在不依赖位置信息的情况下发现相关性。
下面作者介绍了专门处理表格数据的模型SAINT, SAINT用了很多方法来克服在表格数据上训练的困难。SAINT对连续特征也进行了类embedding的处理,把每个numerical的feature 用一个1Xd的dense层+relu 直接投影到d维的embedding空间中,category部分就直接走embedding层,这些新向量作为token传入到Transformer的编码器中,该编码器通过以下两种方式使用注意力:
第一是自注意力,它关注每个数据样本内的个体特征。
第二是样本间注意力,它将一行(即一个数据样本)与其他行相关联。
另外作者还利用了对比式无监督预训练来提高半监督问题的性能。
2. 相关工作
2.1 表格模型
传统处理表格数据的模型是TabTransformer,它使用了transformer的编码器在分类特征上学习上下文嵌入,连续特征被接到嵌入特征中,并送入MLP。该模型的主要问题是连续数据不经过自注意力块。这意味着任何关于分类特征和连续特征之间相关性的信息都会丢失。
在作者的模型中,通过将连续特征和分类特征投影到高维嵌入空间,并送入transformer块来解决这个问题。作者提出了一种新型的注意力机制,允许数据点相互关注,以获得更好的表示。
2.2 轴向注意力
作者提出了样本间注意力,首先进行一个样本点的特征交互,然后样本点与其他样本相互交互。
2.3 自监督学习
在语言和视觉领域,通过在无标记数据上执行 “前置任务 ”并在有标记数据上进行微调来实现自监督。对表格数据进行自监督的前置任务有掩码、去噪和替换令牌检测。
- 掩码(或掩码语言模型MLM)是当个体特征被掩盖时,模型去填充它们的值。
- 去噪会向数据中注入各种类型的噪声,目的是恢复原始值。
- 替换标记检测(RTD)在特征向量中插入随机值,并试图找到这些随机值的位置。
- 对比式预训练,即在最大化两个不同点之间的距离的同时,最小化同一点的两个视图之间的距离。
作者将对比式预训练与去噪相结合,在不同数据集上进行预训练,结果表明该方法优于传统的boosting方法。
3. Self-Attention and Intersample Attention Transformer (SAINT)

假设是第i个样本点的长度为n的特征向量。
是第i个样本点的标签。共m个样本点。我们向每个样本追加一个CLS。这样
。E表示嵌入层,将每个特征嵌入到d维空间中。这样
的形状是n+1,
的形状是(n+1)*d
在表格数据中,不同特征的分布可能是不同的,这就需要一种异构的嵌入方式。作者提出将分类特征、连续特征投影到d维空间,然后再通过Transformer编码器。
3.1 模型结构

SAINT由L个stage组成,每个stage由一个自注意力块和一个样本间注意力块组成。自注意力块由多头自注意力层(h个头)、具有GELU的全连接前馈层、跳跃连接和层归一化组成。样本间注意力块与自注意力块类似,只是将自注意力层换成了样本间注意力层。
有1个stage,一批b个输入的时候,具体公式如下:

3.2 样本间注意力
样本间注意力是一种行注意力,注意力是通过不同数据点之间计算的。具体来说,将单个样本的每个特征串联起来,然后计算各样本间的注意力。这使我们能够通过检查其他点来改进给定点的表示。当某行中某特征缺失或有噪声时,样本间注意力使SAINT能够从其他相似样本中借用相应的特征。
在单个头部中计算样本间注意力的流程如下:

在多头的情况下,将q、k、v投影到 d/h 维上,其中h是头的个数。然后将新向量拼接起来,得到长度为d的向量。
4. 预训练&微调
4.1 数据增强
VIME的作者使用mixup作为数据增强的方法,但这仅限于连续数据。作者在输入空间使用CutMix增强样本,在嵌入空间中使用mixup。

数据增强的公式如下,该公式中,m是一个01掩码向量,α是mixup的参数。在cutmix中,对每一个样本点随机选择另一个样本点
, 利用掩码向量m,第i个样本的部分特征被第a个随机样本对应位上的特征替换掉,得到每个样本点的CutMix版本
。在Mixup中,选择一个新的样本点
, 执行混合。
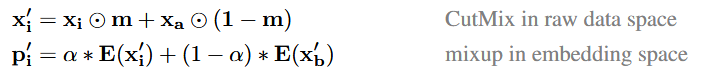
4.2 SAINT和投影头
投影头是由一个隐藏层和一个ReLU组成的。使用投影头可以降低维数,并提高效果。
4.3 损失函数
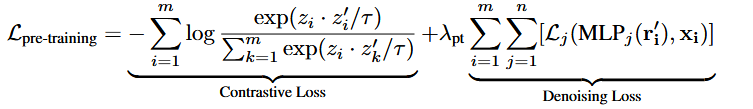
在预训练阶段,损失包含两部分:
(1)对比损失,它鼓励同一数据点的两个视图(zi 和 z′i)接近,鼓励不同点(zi 和 zj,i != j)相互远离。这里作者使用了InfoNCE损失。
(2)去噪损失,我们试图从噪声视图中预测原始数据样本。我们得到 r′i,我们将输入重构为 x′′ i,以最小化原始数据 xi 与重建数据 x''i 之间的差异。这里使用交叉熵损失(特征是离散的)或均方误差(特征是连续的)。
公式中的MLP是由一个隐藏层和一个ReLU组成。共有n个,每个特征对应一个MLP。和
是超参数。
4.4 微调

SAINT使用未标记数据进行预训练,使用标记数据进行微调。在最后的预测步骤中,我们只将与 [CLS] 标记相对应的token通过一个简单的 MLP,该 MLP 有一个带 ReLU 激活的单隐层,从而得到最终输出。最后使用交叉熵或均方误差进行评估。
5. 实验评价
模型变体:SAINT-s变体只有自我注意力,SAINT-i只有样本间注意力。
监督环境中,平均而言,SAINT变体每一个都比所有的基线模型表现更好。
半监督环境中,预训练的SAINT模型(具有自我和样本间的双重注意)表现最好。
嵌入连续数据是重要的,可以显著提高模型的性能。
模型选择:当特征数量很大时,SAINT-i始终优于其他变体。当训练数据点较少且特征较多时,SAINT-i的性能明显优于SAINT-s的。另外,虽然SAINT-i的参数数量远高于SAINT-s,但执行速度比SAINT-s快。
鲁棒性:SAINT和SAINT-i模型比SAINT-s模型更稳健。表明使用行注意力提高了模型对噪声训练数据的鲁棒性。当数据的90%缺失时,SAINT 在对损坏的训练数据进行训练时是可靠的。
批次的大小改变时,我们发现SAINT-i的性能变化较小,与没有样本间注意力成分的SAINT-s相当。























 371
371

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








