【优选算法】1：双指针

目录

一、移动零

二、复写0

三、快乐数

四、盛水最多的容器

五、有效的三角形个数

六、和为S的两个数字

七、三数之和

八、四数之和

一、移动零

题目链接：283. 移动零 - 力扣（LeetCode）

算法思路：

在本题中，我们可以用一个cur指针来扫描整个数组，另一个dest指针用来记录非零数序列的最后一个位置。根据cur在扫描的过程中，遇到的不同情况，分类处理，实现数组的划分。在cur遍历期间，使[0，dest]的元素全部都是非零元素，[dest +1，cur-1]的元素全是零.

算法流程：

1. 初始化cur=0(用来遍历数组），dest=-1（指向非零元素序列的最后一个位置。因为刚开始我们不知道最后一个非零元素在什么位置，因此初始化为-1）
2. cur依次往后遍历每个元素，遍历到的元素会有下面两种情况：
   1. 遇到的元素是0，cur直接++。因为我们的目标是让[dest+1，cur-1]内的元素全都是零，因此当cur遇到0的时候，直接++，就可以让0在cur-1的位置上，从而在[dest1，cur－1]内
   2. 遇到的元素不是0，dest++，并且交换cur位置和dest位置的元素，之后让cur++，扫描下一个元素。
      1. 因为dest指向的位置是非零元素区间的最后一个位置，如果扫描到一个新的非零元素，那么它的位置应该在dest+1的位置上，因此dest先自增1；
      2. dest++之后，指向的元素就是0元素，因此可以交换到cur所处的位置上，实现[0，dest]的元素全部都是非零元素，[dest+1，cur－1]的元素全是零

C++算法代码：

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int dest=-1;
        int cur=0;
        while(cur<nums.size())
        {
            if(nums[cur]!=0)
            {
                swap(nums[++dest],nums[cur]);
            }
            cur++;
           
        }
    }
};

二、复写0

题目链接：1089. 复写零 - 力扣（LeetCode）

算法思路：

如果「从前向后」进行原地复写操作的话，由于的出现会复写两次，导致没有复写的数「被覆盖掉」。因此我们选择「从后往前」的复写策略。
但是「从后向前」复写的时候，我们需要找到「最后一个复写的数」，因此我们的大体流程分两步：
        i．先找到最后一个复写的数；
        ii．然后从后向前进行复写操作。

算法流程：

a.初始化两个指针cur =0，dest=-1；
b.找到最后一个复写的数：
        Ⅰ. 当cur<n的时候，一直执行下面循环：
                判断cur位置的元素：

                        如果是0的话，dest往后移动两位；

                        否则，dest往后移动一位。

                判断dest时候已经到结束位置，如果结束就终止循环；

                如果没有结束，cur++，继续判断。
c. 判断dest是否越界到n的位置：
        Ⅰ. 如果越界，执行下面三步：
                1.n－1位置的值修改成0；

                2. cur向移动一步;

                3.dest向前移动两步。

d．从cur位置开始往前遍历原数组，依次还原出复写后的结果数组：
        Ⅰ. 判断cur位置的值：
                1.如果是0：dest以及dest -1位置修改成0，dest -= 2；
                2.如果非零：dest位置修改成0，dest -=1；
        Ⅱ.cur--，复写下一个位置。

C++算法代码：

class Solution {
public:
    void duplicateZeros(vector<int>& arr) 
    {
        //1.先找到最后一个数
        int cur=0;
        int dest=-1;
        int n=arr.size();
        while(cur<n)
        {
            if(arr[cur]!=0) 
                dest++;
            else 
                dest+=2;
            if(dest>=n-1)
                break;
            cur++;
        }
        //2.处理一下边界情况
        if(dest==n)
        {
            arr[n-1]=0;
            cur--;
            dest-=2;
        }
        //3.从后向前完成复写操作
        while(cur>=0)
        {
            if(arr[cur]==0)
            {
                arr[dest--]=0;
                arr[dest--]=0;
            }else{
                arr[dest--]=arr[cur];
            }
            cur--;
        }
    }
};

三、快乐数

题目链接：202. 快乐数 - 力扣（LeetCode）

算法思路：

为了方便叙述，将「对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和」这一个
操作记为x操作；
题目告诉我们，当我们不断重复x操作的时候，计算一定会「死循环」，死的方式有两种：
        情况一：一直在1中死循环，即1-＞1->1->1.............
        情况二：在历史的数据中死循环，但始终变不到1
由于上述两种情况只会出现一种，因此，只要我们能确定循环是在「情况一」中进行，还是在「情
况二」中进行，就能得到结果。

为什么一个数进行x操作只会有两种情况呢？

简单证明：
a.去一个最大的数9999999999，他进行一个x操作，会变成810，所以给一个数，他进行一个x操作后，它的范围就是[1-810]
b.根据「鸽巢原理」，一个数变化811次之后，必然会形成一个循环；
c.因此，变化的过程最终会走到一个圈里面，因此可以用「快慢指针」来解决

算法流程：

根据上述的题目分析，我们可以知道，当重复执行x操作的时候，数据会陷入到一个循环之中。而「快慢指针」有一个特性，就是在一个圆圈中，快指针总是会追上慢指针的，也就是说他们总会相遇在一个位置上。如果相遇位置的值是，那么这个数一定是快乐数；如果相遇位置不是1的话，那么就不是快乐数。

C++算法代码：

class Solution {
public:
    //返回平方和
    int square(int n)
    {
        int ret=0;
        while(n)
        {
            int tmp=n%10;
            n=n/10;
            ret=ret+tmp*tmp;
        }
        return ret;
    }
    bool isHappy(int n) {
        int slow=n;
        int fast=square(n);

        while(slow != fast)
        {
            slow=square(slow);
            fast=square(fast);
            fast=square(fast);
        }
        return slow==1;
    }
};

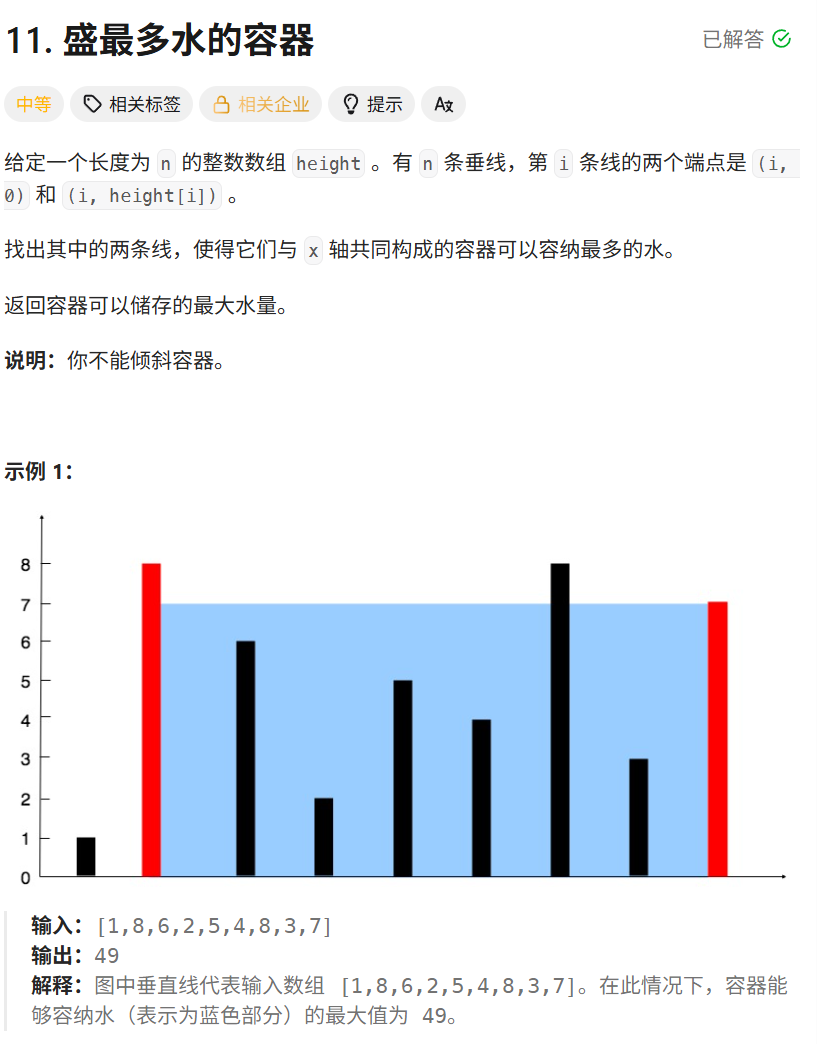
四、盛水最多的容器

题目链接：11. 盛最多水的容器 - 力扣（LeetCode）

解法一：暴力求解（会超时）

枚举出能构成的所有容器，找出其中容积最大的值。
容器容积的计算方式：
设两指针i，j，分别指向水槽板的最左端以及最右端，此时容器的宽度为j－i。由于容器的高度由两板中的短板决定，因此可得容积公式：v=（j－i）*min（height[i]，height[j])

解法一代码：

class Solution {
public:
     int maxArea(vector<int>& height) 
    {
         int n = height.size();
         int ret = 0;
         // 两层 for 枚举出所有可能出现的情况
         for (int i = 0; i < n; i++) 
         {
             for (int j = i + 1; j < n; j++) 
             {
                 // 计算容积，找出最⼤的那⼀个
                 ret = max(ret, min(height[i], height[j]) * (j - i));
             }
         }
         return ret;
    }
};

解法二（双指针）：

算法思路：

设两个指针left，right分别指向容器的左右两个端点，此时容器的容积：
        V =(right - left) * min（height[right]，height[left])
容器的左边界为height[left]，右边界为height[right]。
为了方便叙述，我们假设「左边边界」小于「右边边界」。
如果此时我们固定一个边界，改变另一个边界，水的容积会有如下变化形式：
        容器的宽度一定变小。
        由于左边界较小，决定了水的高度。如果改变左边界，新的水面高度不确定，但是一定不会超过右边的柱子高度，因此容器的容积可能会增大。
        如果改变右边界，无论右边界移动到哪里，新的水面的高度一定不会超过左边界，也就是不会超过现在的水面高度，但是由于容器的宽度减小，因此容器的容积一定会变小的。
由此可见，左边界和其余边界的组合情况都可以舍去。所以我们可以1eft++跳过这个边界，继
续去判断下一个左右边界。

当我们不断重复上述过程，每次都可以舍去大量不必要的枚举过程，直到left与right相遇。期间产生的所有的容积里面的最大值，就是最终答案。

C++算法代码：

class Solution {
public:
    int maxArea(vector<int>& height) {
        int left=0,right=height.size()-1,ret=0;
        while(left<right)
        {
            int e=min(height[left],height[right])*(right-left);
            ret=max(ret,e);
            if(height[left]<height[right])
                left++;
            else 
                right--;
        }
        return ret;
    }
};

五、有效的三角形个数

题目链接：611. 有效三角形的个数 - 力扣（LeetCode）

解法一：暴力求解（会超时）

三层for循环枚举出所有的三元组，并且判断是否能构成三角形。
虽然说是暴力求解，但是还是想优化一下：
判断三角形的优化：

• 如果能构成三角形，需要满足任意两边之和要大于第三边。但是实际上只需让较小的两条边之和大于第三边即可。
• 因此我们可以先将原数组排序，然后从小到大枚举三元组，一方面省去枚举的数量，另一方面方便判断是否能构成三角形

解法一代码：

class Solution {
public:
	int triangleNumber(vector<int>& nums) {
		// 1. 排序
		sort(nums.begin(), nums.end());
		int n = nums.size(), ret = 0;
		// 2. 从⼩到⼤枚举所有的三元组
		for (int i = 0; i < n; i++) {
			for (int j = i + 1; j < n; j++) {
				for (int k = j + 1; k < n; k++) {
					// 当最⼩的两个边之和⼤于第三边的时候，统计答案
					if (nums[i] + nums[j] > nums[k])
						ret++;
				}
			}
		}
		return ret;
	}
};

解法二（双指针）：

算法思路：

先将数组排序。
根据「解法一」中的优化思想，我们可以固定一个「最长边」，然后在比这条边小的有序数组中找出一个二元组，使这个二元组之和大于这个最长边。由于数组是有序的，我们可以利用「对撞指针」来优化。
设最长边枚举到c位置，区间[left，right]是c位置左边的区间（也就是比它小的区间）：

• 如果nums[left]+ nums[right]>nums[c]」：
  • 说明（[left，right一1]区间上的所有元素均可以与nums[right]构成比nums[c]大的二元组
  • 满足条件的有right -left种
  • 此时right位置的元素的所有情况相当于全部考虑完毕，right--，进入下一轮判断
• 如果nums[left]+ nums[right]<= nums[c]：
  • 说明left位置的元素是不可能与[left+1，right]位置上的元素构成满足条件的二元组        
  • left位置的元素可以舍去，left++进入下轮循环

解法二代码：

class Solution {
public:
    int triangleNumber(vector<int>& nums) {
        sort(nums.begin(),nums.end());
        int count=0;
        for(int c=nums.size()-1;c>=2;c--)
        {
            int left=0;
            int right=c-1;
            while(left<right)
            {
                if(nums[left]+nums[right]>nums[c])
                {
                    count+=right-left;
                    right--;
                }
                else{
                    left++;
                }
            }
        }
        return count;
    }
};

六、和为S的两个数字

题目链接：LCR 179. 查找总价格为目标值的两个商品 - 力扣（LeetCode）

解法一：暴力求解（会超时）

两层for循环：

• 外层for循环依次枚举第一个数a；
• 内层for循环依次枚举第二个数b，让它与a匹配;

        ps：这里有个魔鬼细节：我们挑选第二个数的时候，可以不从第一个数开始选，因为前面的数我们都已经在之前考虑过了；因此，我们可以从a往后的数开始列举。

• 然后将挑选的两个数相加，判断是否符合目标值。

解法一代码：

class Solution {
public:
	vector<int> twoSum(vector<int>& nums, int target) {
		int n = nums.size();
		for (int i = 0; i < n; i++) { // 第⼀层循环从前往后列举第⼀个数
			for (int j = i + 1; j < n; j++) { // 第⼆层循环从 i 位置之后列举第⼆个
				数
					if (nums[i] + nums[j] == target) // 两个数的和等于⽬标值，说明我们
						已经找到结果了
						return { nums[i], nums[j] };
			}
		}
		return { -1, -1 };
	}
};

解法二：双指针

算法思路：

a.初始化left，right分别指向数组的左右两端（这里不是我们理解的指针，而是数组的下标)
b.当leftくright的时候，一直循环

         i. 当nums[left]+nums[right]== target时，说明找到结果，记录结果，并且返回;

         ii.当nums[left] + nums[right]<target时:

                对于nums[left]而言，此时nums[right]相当于是nums[left]能碰到的最大值（别忘了，这里是升序数组哈~）。如果此时不符合要求，说明在这个数组里面，没有别的数符合nums[left]的要求了（最大的数都满足不了你，你已经没救了）。因此，我们可以大胆舍去这个数，让left++，去比较下一组数据；

                那对于nums[right]而言，由于此时两数之和是小于目标值的，nums[right]，还可以选择nums[left]大的值继续努力达到目标值，因此right指针我们按兵不动；

iii.当nums[left]+nums[right]>target时，同理我们可以舍去nums[right]（最小的数都满足不了你，你也没救了）。让right-，继续比较下一组数据，而left指针不变（因为他还是可以去匹配nums[right]更小的数的）。

解法二代码：

class Solution
{
public:
	vector<int> twoSum(vector<int>& nums, int target)
	{
		int left = 0, right = nums.size() - 1;
		while (left < right)
		{
			int sum = nums[left] + nums[right];
			if (sum > target) right--;
			else if (sum < target) left++;
			else return { nums[left], nums[right] };
		}
		// 照顾编译器
		return { -1, -1 };
	}
};

七、三数之和

题目链接：15. 三数之和 - 力扣（LeetCode）

算法思路：

本题与两数之和类似，是非常经典的面试题。
与两数之和稍微不同的是，题目中要求找到所有「不重复」的三元组。那我们可以利用在两数之和那里用的双指针思想，来对我们的暴力枚举做优化：
        i.先排序；
        ii.然后固定一个数a：
        iii.在这个数后面的区间内，使用「双指针算法」快速找到两个数之和等于a即可。
但是要注意的是，这道题里面需要有「去重」操作~
        i．找到一个结果之后，left和right指针要「跳过重复」的元素;
        ii.当使用完一次双指针算法之后，固定的a也要「跳过重复」的元素。

C++算法代码：

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        sort(nums.begin(),nums.end());
        vector<vector<int>> ret;
        int i=0;
        int n=nums.size();
        while(i<=n-3)
        {
            int left=i+1;
            int right=n-1;
            while(left<right)
            {
                if(nums[left]+nums[right]>-nums[i])
                {
                    right--;
                }else if(nums[left]+nums[right]<-nums[i])
                {
                   left++; 
                }else
                {
                    vector<int> v={nums[left],nums[right],nums[i]};
                    ret.push_back(v);
                    left++;
                    while(left<right&&nums[left-1]==nums[left])
                    {
                        left++;
                    }
                    right--;
                    while(left<right&&nums[right+1]==nums[right])
                    {
                        right--;
                    }
                }
                
            }
            i++;
            while(i<=n-3&&nums[i-1]==nums[i])
            {
                i++;
            }
            
        }
        return ret;
    }
};

八、四数之和

题目链接：​​​​​​​18. 四数之和 - 力扣（LeetCode）

算法思路：

a.依次固定一个数a1；
b.在这个数a的后面区间上，利用「三数之和」找到三个数，使这三个数的和等于target-a即可。

C++算法代码：

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        vector<vector<int>> ret;
        sort(nums.begin(),nums.end());
        int n=nums.size();
        int a1=0;
        while(a1<=n-4)
        {
            int a2=a1+1;
            while(a2<=n-3)
            {
                int left=a2+1;
                int right=n-1;
                long long aim=(long long)target-nums[a2]-nums[a1];
                while(left<right)
                {
                    int sum=nums[left]+nums[right];
                    if(sum<aim)
                    {
                        left++;
                    }else if(sum>aim)
                    {
                        right--;
                    }else
                    {
                        ret.push_back({nums[a1],nums[a2],nums[left],nums[right]});
                        left++,right--;
                        while(left<right&&nums[left-1]==nums[left]) left++;
                        while(left<right&&nums[right+1]==nums[right]) right--;
                    }
                }
                a2++;
                while(a2<=n-3&&nums[a2-1]==nums[a2]) a2++;
            }  
            a1++;
            while(a1<=n-4&&nums[a1-1]==nums[a1]) a1++;  
        }
        return ret;
    }
};