【深度图像拼接学习01】基础概念学习_图像拼接深度学习-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_62140542/article/details/143831965

最近在进行毕业设计，阅读paper过程中，遇到了挺多专业名词的，由于之前对拼接领域不算太熟悉，因此有些概念上不太清楚，今天开个坑来更新相关内容。

基础线性变换（basic linear tranform）

最早接触和这个词是在pytorch方法中的transforms见过，具体涉及过程就如下所示了。

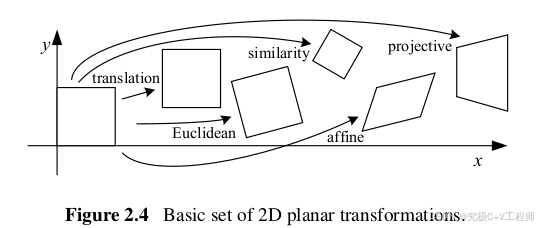
标几种2D平面变换。引自《Computer Vision: Algorithms and Applications》题

（1）translation：

所有点的坐标均发生相同的偏移，其式如下：

$\left\{\begin{array}{l}x^{\prime}=x+\Delta x\\y^{\prime}=y+\Delta y\end{array}\right.$

矩阵形式：

$\boldsymbol{x}=\begin{bmatrix}1&0&\Delta x\\0&1&\Delta y\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix}$

（2）Euclidean:

旋转，将平面上每一个点用极坐标的形式进行表示：

$$\begin{cases}x=rcos\alpha\\y=rsin\alpha&&\end{cases}$$

实际本质就是以原点为圆心，将点$(x,y)$旋转$\theta$角度，最后的坐标可表示为：

$$\begin{aligned}&(rcos(\alpha+\theta),\:rsin(\alpha+\theta))\\&=\quad(rcos\alpha cos\theta-rsin\alpha sin\theta,\:rsin\alpha cos\theta+rcos\alpha sin\theta)\\&=\quad(xcos\theta-ysin\theta,\:xsin\theta+ycos\theta)\end{aligned}$$

使用矩阵形式表示旋转+平移如下：

$$\boldsymbol{x}=\begin{bmatrix}cos\theta&-sin\theta&\Delta x\\sin\theta&cos\theta&\Delta y\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix}$$

（3）similarity

本质关系就是将坐标扩大 $\alpha$ 倍，公式如下：

$$x,y \rightarrow \alpha x,\alpha y$$

缩放+旋转+平移矩阵形式如下：

$$ \boldsymbol{x}=\begin{bmatrix}\alpha cos\theta&-\alpha sin\theta&\Delta x\\\alpha sin\theta&\alpha cos\theta&\Delta y\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix}=\begin{bmatrix} a& -b&\Delta x \\ b&a&\Delta y \end{bmatrix} \begin{bmatrix} x\\ y\\ 1 \end{bmatrix} $$

（4）affine

不改变2D平面平行关系，实际就是做了一次线性变换

$$\left\{
\begin{aligned}
x_{0}' = a_{0}x+b_{0}y+c_{0}\\
x_{1}' = a_{1}x+b_{1}y+c_{1}\\
\end{aligned}
\right.$$

矩阵形式如下：

$$\boldsymbol{x} =\begin{bmatrix} a_{0}&b_{0}&C_{0}\\ a_{1}&b_{1}&C_{1}\end{bmatrix}
\begin{bmatrix}x\\y\\1\end{bmatrix}$$

(5) projective投影

也称作透视变换或同态映射，其作用在齐次坐标上

$$\boldsymbol{x'}=Hx = \begin{bmatrix}a_{0}&b_{0}&c_{0}\\a_{1}&b_{1}&c_{1}\\ a_{2}&b_{2}&c_{2}\\\end{bmatrix} \begin{bmatrix} x\\y\\1\end{bmatrix}$$

单应性矩阵（Homography matrix）

概念：即上述projective使用的矩阵，

大基线、小基线

‌大基线图像和小基线图像的主要区别在于拍摄时两个摄像机之间的距离。‌

‌ 小基线图像‌：当两个摄像机之间的距离较近时，拍摄得到的图像称为小基线图像。这种情况下，摄像机的位置变化较小，焦距和其他内参数变化也不大，对应点的邻域相似‌。

‌ 大基线图像‌：当两个摄像机之间的距离较远时，拍摄得到的图像称为大基线图像。这种情况下，摄像机的位置变化较大，焦距和其他内参数可以有较大的变化，导致图像之间的差异较大。

掩码

在图像处理中中，掩码（Mask）是一种特殊的图像，用于指定对原始图像进行操作的区域。掩码通常是二值图像（即图像上的每个像素只有两个可能的值，通常是0和255，分别代表黑色和白色），但也可以是灰度图像或多通道图像，尽管二值掩码最为常见。

其他：

像素（Pixel）：图像的最基本单元，每个像素都有一个或多个与其关联的数值，这些数值决定了像素的颜色和亮度等信息。
分辨率（Resolution）：图像的清晰度或细节水平，通常用每英寸像素数（PPI，Pixels Per Inch）或每厘米像素数来衡量。高分辨率意味着图像包含更多的细节。
图像增强（Image Enhancement）：提高图像视觉效果或改进图像质量，以便更容易或更准确地进行图像分析的过程。
仿射变换（Affine Transformation）：保持图像中“直线”仍为“直线”和“平行线”仍为“平行线”的变换，包括旋转、平移、缩放等。
插值（Interpolation）：在图像缩放、旋转等操作时，用于估算新像素位置处像素值的方法。
动态范围（Dynamic Range）：图像中最亮和最暗部分之间的亮度比值。动态范围越大，图像能够展现的细节就越多。
色调映射（Tone Mapping）：一种将高动态范围（HDR）图像转换为低动态范围（LDR）图像的技术，同时保持图像中的视觉信息。
色彩空间（Color Space）：描述和表示图像中颜色的数学模型。常见的色彩空间包括RGB、CMYK、HSV和Lab等。
色彩校正（Color Correction）：调整图像颜色的过程，以改善其视觉效果或使其符合特定的色彩标准。
图像配准（Image Registration）：将两幅或多幅图像对齐的过程，以便进行后续的比较、组合或分析。
超分辨率重建（Super-Resolution Reconstruction）：从低分辨率图像中恢复高分辨率图像的技术，常用于改善图像质量和细节。
图像融合（Image Fusion）：将多幅图像的信息融合到一幅图像中，以提高图像的清晰度、对比度或包含的信息量。
纹理分析（Texture Analysis）：对图像中纹理特征进行提取和分析的过程，常用于材料科学、医学图像处理和遥感等领域。
图像恢复（Image Restoration）：从退化的图像中恢复原始图像的过程，退化可能由噪声、模糊、失真等因素引起。
图像编码（Image Coding）：对图像数据进行压缩编码的过程，以便于存储和传输。常见的图像编码标准包括JPEG、PNG和WebP等。
全景图像拼接（Panoramic Image Stitching）：将多幅部分重叠的图像拼接成一幅宽视角的全景图像的技术。