毕业设计准备（1）：密度聚类算法(Matlab)

毕业设计准备（1）：密度聚类算法(Matlab)

一、算法原型

1.1基本解释

密度聚类(Density-Based Spatial Clustering of Applications with Noise，DBSCAN)是一种基于密度的聚类算法，该算法假设样本类别可根据样本分布的密集度 进行判断。DBSCAN算法主要是通过数据类别的密度连通性快速识别任意形状的 簇，将具有足够密度的区域划分为簇。该算法可以发现任意形状和数量的簇，通 过聚类将样本数据划分成不同的簇类。
DBSCAN 算法中数据点可以分为以下三类：

(1)核心对象：若样本 xi 的e邻域内至少包含 MinPts 个样本，即称样本 点xi为核心对象。
(2)边界点：若样本点 xi 的e邻域范围内包含的样本数目小于MinPts ，但是 它在其他核心对象的邻域内，则称样本点xi为边界点。
(3)噪声点：不属于任何一个簇Ci 的离散点。

DBSCAN 算法中基本概念如下：

(1)密度直达：如果xi位于xj的邻域内，且xj为核心对象，则称xi由xj密 度直达，反之不一定成立。
(2)密度可达：若存在核心对象(x2,x3,···,xn−1),且x1 至x2密度直达，x2至x3 密度直达，···，xn−2 至 xn−1 密度直达，xn−1 至 xn 密度直达，则 x1 到 xn 密度 可达。密度可达不具备对称性。
(3)密度相连：若存在核心对象 xi，使得 xi 到 xj 和 xk 都密度可达， 则xj 和 xk 都密度相连。密度相连具有对称性质，如果xj 和xk 密度相连，那 么xk 和xj 也一定密度相连，密度相连的两个点属于同一个聚类簇。
(4)非密度相连：如果两个点不属于密度相连关系，则两个点非密度相连。

1.2问题锚点

实行以上算法需要解决以下几点：
（1）判断样本 xi 的e邻域内是否至少包含 MinPts 个样本；
（2）将包含在xi内的点和其子包含的所有点组成一组；
（3）在运行中要解决运行的速度和内存问题；
（4）参数怎么设置合理；

1.3解决思路

（1）对于1.2（3）问题可以使用矩阵计入点与点的信息，后续操作可以通过对矩阵进行操作以减少运行的速度和内存问题。
（2）对于1.2（1）问题可以先对数据进行标准化处理，再求出2点之间的距离,得到N*N邻接的距离矩阵D，在matlab中有函数pdist2(x1,x2)计算两点之间的距离。
下面是一个简单的例子，演示如何使用 pdist2 计算两个点集之间的距离：

x1 = [1 2; 3 4];
x2 = [5 6; 7 8];
D = pdist2(x1, x2, 'euclidean');

所以邻接的距离矩阵D可以为

%标准化数据
Date = normalize(date, 'range');
%邻接矩阵
D = pdist2(Date,Date);

而对于判断样本 xi 的e邻域内是否至少包含 MinPts 个样本就可以将邻接矩阵中“小于e且不等于0的地方用1表示，其他用0表示”记入矩阵D_K,D_K又可以叫邻接矩阵。

D_K =zeros(size(D,1),size(D,1));
D_K(D_d<epsilon & D_d ~=0) =1;

D_K对列求和就可以得到一个点与多少个点相连，小于等于MinPts且不等于就可以分为边界集K_C，等于0就可以分为噪声集F_C，大于就可以分为核心集Y_C。

F_C =D_N(2,D_N(1,:)==0);
Y_C =D_N(2,D_N(1,:)>MinPts);
K_C =D_N(2,D_N(1,:)<=MinPts & D_N(1,:)~=0);

以上就可以对数据进行分类、求出邻接的距离矩阵D和邻接矩阵D_K。
（3）对于1.2（2）问题，就可以利用邻接矩阵D_K，使用图论中的无向图就可以对点进行分类。具体方法如下：

% 创建图对象
G = graph(D_K);

% 找到连通分量
[bin, binsize] = conncomp(G);
% 初始化元胞数组
components = cell(max(bin), 1);

% 将每个连通分量的节点存储到元胞数组中
for i = 1:max(bin)
    components{i} = find(bin == i);
end

%第一类
C1 =components{1};

简述
这个算法的主要目标是通过邻接矩阵构建一个图，并找到图中的所有连通分量，然后将每个连通分量的节点存储到一个元胞数组中。主要步骤包括：

1. 根据邻接矩阵构建图对象。
2. 使用 conncomp 函数找到图中的所有连通分量。
3. 将每个连通分量的节点存储到元胞数组中。
4. 提取特定连通分量的节点。
   这个算法的时间复杂度主要由 conncomp 函数决定，通常是 O(n+m)，其中 n 是顶点数量，m 是边的数量。空间复杂度主要由邻接矩阵和元胞数组决定，通常是 O(n2)。

二、研究数据

2.1导入数据

本文采用SCADA数据进行深入的统计建模分析。通过对机组的运行状况、风速、等关键部件温度等多维度数据的关联性进行挖掘，并结合风机的运行理论和先进的统计建模技术。

数据链接：
项目首页 - 风电机组运行完整数据集:风电机组运行完整数据集 - GitCode

下载好数据后再main.m文件中导入数据：

clear,clc;
% WINDSPEED: 预测风速
% WINDDIRECTION: 风向
% TEMPERATURE: 温度
% HUMIDITY: 湿度
% PRESSURE: 气压
% PREPOWER: 预测功率（系统生成）
% ROUND(A.WS1): 实际风速
% ROUND(A.POWER0): 实际功率
% YD15: 已有实际功率预测目标
T11 = importfile1("C:\Users\斌\Desktop\风能发电机\数据\e3850-main\data\11.csv", [2, Inf]);
A = [T11.ROUNDAWS1(:),T11.ROUNDAPOWER0(:)];
a = A(A(:,2)<1,:);
date = A(A(:,2)>0,:);

%绘图
figure(1)
subplot(2,2,1)
scatter(date(:,1),date(:,2),'b*');
title("风速与实际功率的关系");
xlabel("风速km/h");
ylabel("实际功率kw/h");
subplot(2,2,2)
histogram(date(:,1))
subplot(2,2,3)
histogram(date(:,2))
subplot(2,2,4)
scatter(a(:,1),a(:,2),'*');

2.2数据描述

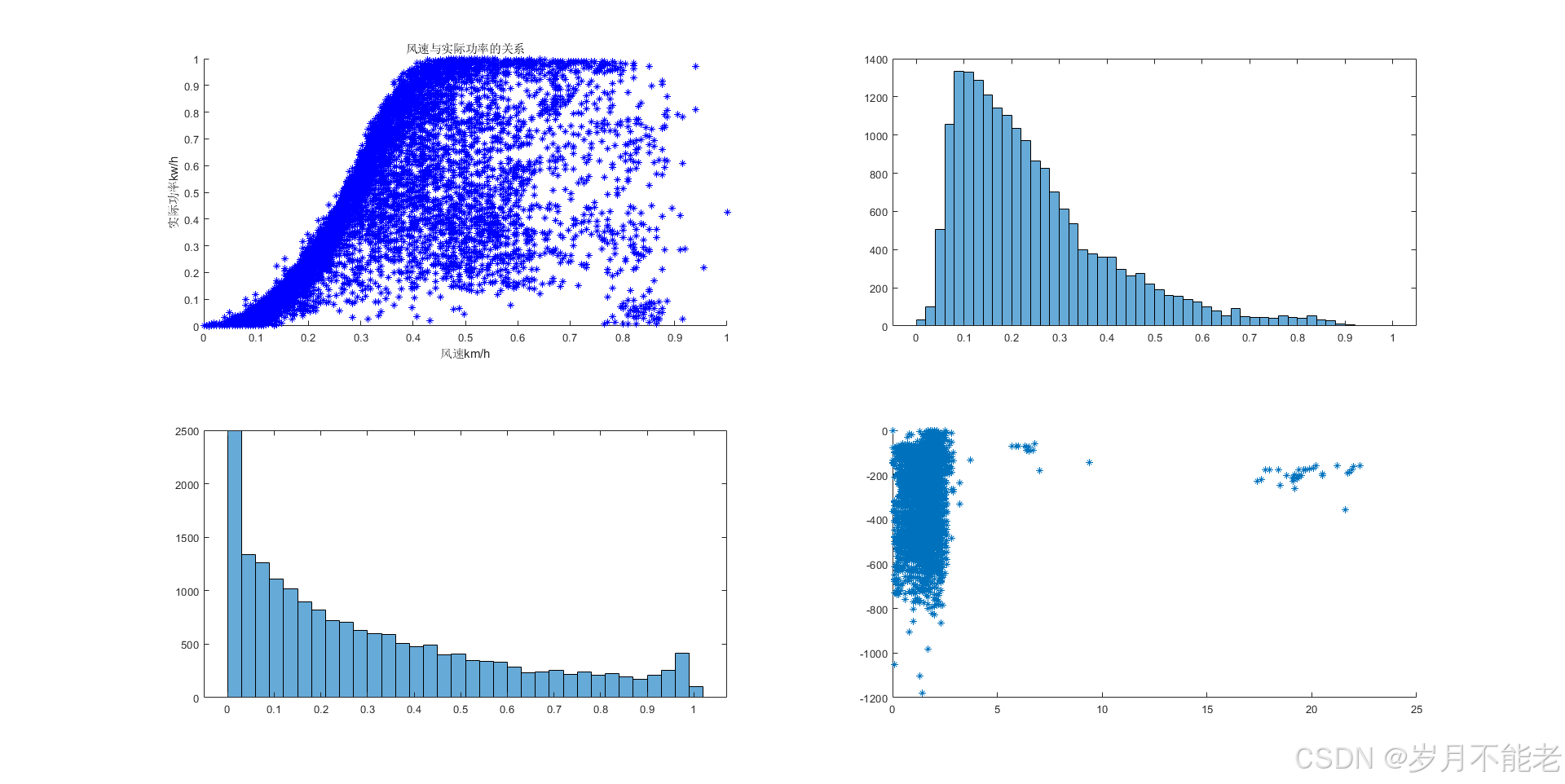
由2.1代码展示可以看出：
（1）数据比较杂乱，需要进行筛选。
（2）大部分数据有聚成一块的现象，少部分数据独立。

2.3密度聚类算法

Date = normalize(data, 'range');
D = pdist2(Date,Date);
%密度聚类
epsilon =0.0225;
MinPts =15;
D_d =D;D_l =1:size(D,1);
D_K =zeros(size(D,1),size(D,1));
D_K(D_d<epsilon & D_d ~=0) =1;

% 创建图对象
G = graph(D_K);

% 找到连通分量
[bin, binsize] = conncomp(G);
% 初始化元胞数组
components = cell(max(bin), 1);

% 将每个连通分量的节点存储到元胞数组中
for i = 1:max(bin)
    components{i} = find(bin == i);
end

C1 =components{1};

D_N =[sum(D<epsilon)-1;1:size(D,1)];
F_C =D_N(2,D_N(1,:)==0);
Y_C =D_N(2,D_N(1,:)>MinPts);
K_C =D_N(2,D_N(1,:)<=MinPts & D_N(1,:)~=0);

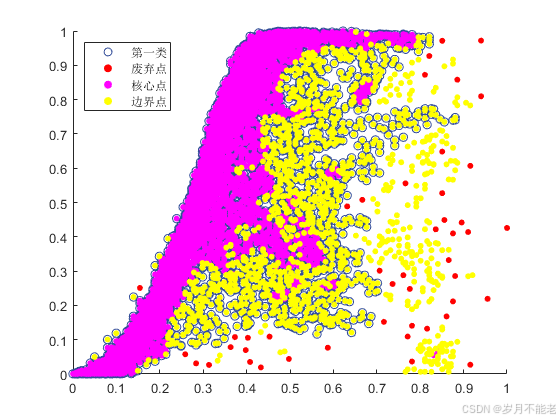
%聚类可视化
figure(2)
hold on
scatter(Date(C1,1), Date(C1,2), 40, [0.2 0.3 0.6]);
scatter(Date(F_C,1), Date(F_C,2), 20, [1 0 0], 'filled');
scatter(Date(Y_C,1), Date(Y_C,2), 20, [1 0 1], 'filled');
scatter(Date(K_C,1), Date(K_C,2), 20, [1 1 0], 'filled');
legend('第一类','废弃点', '核心点', '边界点','Location', 'northwest'); % 将图例放在左上角
hold off

       

3.总结与评价

（1）密度聚类算法是一种基于密度的聚类方法，能够识别任意形状的簇并有效处理噪声。其核心是通过局部密度来划分簇，常见的算法如DBSCAN、OPTICS和Mean-Shift各有特点。
（2）DBSCAN通过核心点和邻域扩展簇，适合不同形状的簇，对参数敏感；在Matlab中实现时，需根据数据特点调整参数以优化聚类效果。