【算法分析与设计】第四章-双连通图与关节点识别

什么是关节点

    关节点按字面理解，充当”关节“的点。假设无向图G连通，当删除该点及其关联的边后G不再连通，则称该节点为关节点。（把你波了盖砍掉，你还和你的小腿连通吗？？）
举例：下图中的1号点就是一个关节点。

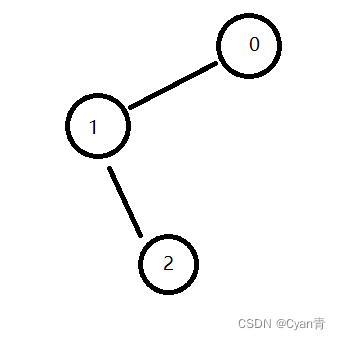
双连通

    双连通，顾名思义，双向连通，G中任意两个结点通达的路径不止一条。也就是任意两结点间的路径可以构成回路。这样删除G中的任意结点后，原图还是连通的。（此路不通，换条路呗）换句话说，不含关节点的连通图就是双连通图。
举例：下图就是一个双连通图，不含有关节点。

值得注意的是：下图情况也符合双连通图的定义。砍掉0后，1自己还是连通的。

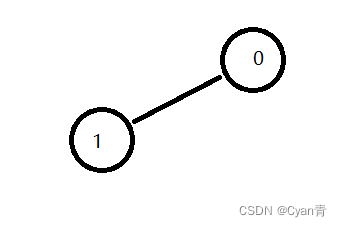
关节点的识别

此处涉及：DFS, 时间戳，深度优先树，树边，反向边等概念。
简要介绍：
深度优先树：顾名思义，深度优先搜索生成的树
树边：gmsy，图G中属于深度优先树的边
反向边：G中不属于深度优先树的边，后裔指向祖先的边
给出规律：一个无向图的深度优先树只包含树边和反向边。
一个结点是关节点当且仅当：

1. 该结点是root且其至少有两个孩子
2. 该结点非root，则其某棵子树上不含指向该结点祖先的反向边

• 关键代码：

memset(d, -1,sizoef d);
void DFS(int u, int p){	//当前结点u， 父亲p
	Low[u] = d[u] = tm ++;	//d[]是时间戳，代表当前结点是第几个访问的，Low[]表示该节点所能追溯到的最早访问的祖先。
	for(ENode*w = a[u]; w; w = w->nextarc){
		int v = d->adjVex;
		if(d[v] != -1){
			DFS(v, u);
			Low[u] = min(Low[u], Low[v]); 	//当子树有反向边时，更新该节点的Low值
		}
		else
			if(v != p && Low[u] > d[v]) Low[u] = d[v];	//当前结点的反向边
	}
}

通过Low[]，与d[]数组我们可以间接判断是否是关节点。若想直接识别，对上面代码略作修改。

void DFS(int u, int p){	//当前结点u， 父亲p
	bool flag  = false; //判断有不含指向u祖先的反向边的子树
	int cnt = 0;	//统计子树数目
	Low[u] = d[u] = tm ++;	//d[]是时间戳，代表当前结点是第几个访问的，Low[]表示该节点所能追溯到的最早访问的祖先。
	for(ENode*w = a[u]; w; w = w->nextarc){
		int v = d->adjVex;
		if(d[v] != -1){
			DFS(v, u);
			Low[u] = min(Low[u], Low[v]); 	//当子树有反向边时，更新该节点的Low值
			if(Low[v]  >= d[u]) flag = true;
			cnt ++; 	//统计孩子数
		}
		else
			if(v != p && Low[u] > d[v]) Low[u] = d[v];	//当前结点的反向边
	}
	//结点分类讨论
	if(flag && u || u == 0 && cnt > 1) cout << u << "是关节点" << endl;
}