深度优先搜索dfs算法刷题笔记【蓝桥杯】_蓝桥杯深度优先 4个方向搜索-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_61786525/article/details/127272014

本文深入浅出地介绍了深度优先搜索（DFS）算法的实际应用，包括走出迷宫、N皇后问题等经典题目，并提供了详细的代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

其实网上已经有不少dfs的算法笔记，但我之所以还再写一篇，主要是因为我目前见到的笔记，都有些太偏向理论了。
对于基础薄弱的或是没有基础的人（like me），有点不合适，因为看了，也不能说自己会了。
所以这篇主要是实践（题目）出发

理论

为了求得问题的解，先选择某一种可能情况向下继续递归
在这个过程中，当发现原来的选择是错误的，就退回一步重新选择，继续向下探索
反复进行这个操作，直到出现结果、无解或者是遍历完毕

实践

走出迷宫

题目描述

小明现在在玩一个游戏，游戏来到了教学关卡，迷宫是一个N*M的矩阵。
小明的起点在地图中用“S”来表示，终点用“E”来表示，障碍物用“#”来表示，空地用“.”来表示。
障碍物不能通过。小明如果现在在点（x，y）处，那么下一步只能走到相邻的四个格子中的某一个：（x+1，y），（x-1，y），（x，y+1），（x，y-1）；
小明想要知道，现在他能否从起点走到终点。

输入描述

本题包含多组数据。
每组数据先输入两个数字N,M
接下来N行，每行M个字符，表示地图的状态。
数据范围：
2<=N,M<=500
保证有一个起点S，同时保证有一个终点E.

输出描述

每组数据输出一行，如果小明能够从起点走到终点，那么输出Yes，否则输出No

示例一
输入

3 3
S..
..E
...
3 3
S##
###
##E

输出

Yes
No

解析

这道题是一道非常标准的题，很好地帮助你理解深度优先搜索
算法思想：从S开始，往右进行dfs（不一定要右，可以根据自己需要），右边的是 . 符合条件，所以进入右边的这个点 . 然后从这个点开始继续dfs，下一个点如果不符合条件就回退到这个点
具体的放在代码里说

题解

#include<bits/stdc++.h>
using namespace std;
char maze[510][510];
bool vis[510][510];
int dir[4][2]={{1,0},{0,1},{-1,0},{0,-1}};
int N,M;
bool in(int n,int m){
    return 0<n&&n<=N&&0<m&&m<=M;                         //基础的判断，是否会越界
}
bool dfs(int n,int m){
    if(maze[n][m]=='E') return true;                                 //return条件
    for(int i=0;i<4;++i){
       int a=n+dir[i][0],b=m+dir[i][1];                                //走上下左右方向
       if(!vis[a][b]&&in(a,b)&&maze[a][b]!='#'){               //vis[][]表示是否走过
           vis[n][m]=1;
           if(dfs(a,b)) return true;
   }
    }
    return false;                                  
}
int main(){
    int y,x;
    while(cin>>N>>M){
        memset(vis,0,sizeof(vis));
        getchar();
        for(int i=1;i<=N;++i){
            for(int j=1;j<=M;++j){
                scanf("%c",&maze[i][j]);
                if(maze[i][j]=='S') y=i,x=j;
            }
            getchar();
        }
        if(dfs(y,x)) printf("Yes\n");
        else printf("No\n");
    }
}

N皇后问题

题目描述

给出一个n×n的国际象棋棋盘，你需要在棋盘中摆放n个皇后，使得任意两个皇后之间不能互相攻击。具体来说，不能存在两个皇后位于同一行、同一列，或者同一对角线。请问共有多少种摆放方式满足条件

输入描述

一行，一个整数n(1≤n≤12)，表示棋盘的大小。

输出描述

输出一行一个整数，表示总共有多少种摆放皇后的方案，使得它们两两不能互相攻击。

示例一
输入

4

输出

2

解析

这道题是dfs+回溯（因为如果出现皇后不难放的情况需要回退到上一步），有点像 走出迷宫 的变式（只不过限制不能搜索的条件变化了一些）
设计dfs算法：
1. 设置return条件，当摆了n个皇后时，就要将方案数+1，并且返回。或者是当搜索的行数超过给出的n行
2. 进行向下搜索的设计：不能与之前的皇后出现同行、同列或者同对角线，所以可以将之前的皇后用遍历的方式放在各个位置，目前的皇后设置判断不与之前的皇后出现限制。给之前的皇后的位置标记。如果没破坏限制，就将目前的皇后放在相应位置，拿下一个皇后，继续向下搜索

题解

#include<bits/stdc++.h>
using namespace std;
int n,ans=0,num=0;
bool a=true;
int column[15];
void dfs(int row){          //放进来row行数的参数
    if(num==n){
        ++ans;
        return;
    }
    if(row==n+1) return;        //return条件
    for(int i=1;i<=n;++i){       //遍历每一列
        for(int j=1;j<row;++j){       //遍历这一行以上的所有行（这一行是准备放目前的皇后的行）
            if(column[j]==i||(row-j==abs(column[j]-i))) {      //column[]是记录之前皇后的位置，key是行数，value是列数
                a=false; 
                break;
            }
        }
        if(a){
            column[row]=i;                 //如果可以放，就标记这个位置
            ++num;                            //将已经放了的皇后数+1
            dfs(row+1);
            --num;
            column[row]=0;
        }
        a=true;
    }
}
int main(){
    cin>>n;
    dfs(1);
    cout<<ans;
}

[蓝桥杯 2017 省 A] 正则问题

考虑一种简单的正则表达式：

只由 x ( ) | 组成的正则表达式。

小明想求出这个正则表达式能接受的最长字符串的长度。

例如 ((xx|xxx)x|(x|xx))xx 能接受的最长字符串是： xxxxxx，长度是 $6$ 。

输入格式

一个由 x()| 组成的正则表达式。输入长度不超过 $100$ ，保证合法。

输出格式

这个正则表达式能接受的最长字符串的长度。

样例输入 #1

((xx|xxx)x|(x|xx))xx

样例输出 #1

思路

我写这道题的时候一开始真没看懂什么意思，看了一会儿才明白了：进“（（”是优先顺序，遇到“ | ”是需要停下进行最长字符长度的判断 —— （（xx | xxx）x | （x | xx））xx 首先xx遇到了" | "，然后再xxx，那么sum=max(2,3)，ans=max(ans,sum)。最长ans更新为3。之后是x，那就是sum=3+1，之后遇到“ | ”，ans=max(ans,sum)。后面的以此类推
使用dfs，遇到“（”就进入一层dfs，记录左侧x的长度，然后遇到 “ | ”就记录右边x的长度，直到“ | ”或者“）”遇到“）”退出这一层dfs，结算ans

题解

#include<bits/stdc++.h>
using namespace std;
string str;
int pos,len;
int dfs(){
	int num=0,ans=0;
	while(pos<len){
		if(str[pos]=='('){
			pos++;
			num+=dfs();
		}
		else if(str[pos]==')'){
			pos++;
			break;
		}
		else if(str[pos]=='|'){
			pos++;
			ans=max(num,ans);
			num=0;
		}
		else{
			num++;
			pos++;
		}
	}
	ans=max(num,ans);
	return ans;
}
int main(){
	cin>>str;
	pos=0,len=str.length();
	cout<<dfs()<<endl;
}

[蓝桥杯 2018 省 AB] 全球变暖

你有一张某海域 $\times N$ 像素的照片，. 表示海洋、 # 表示陆地，如下所示：

.......
.##....
.##....
....##.
..####.
...###.
.......

其中 “上下左右” 四个方向上连在一起的一片陆地组成一座岛屿。例如上图就有 $2$ 座岛屿。

由于全球变暖导致了海面上升，科学家预测未来几十年，岛屿边缘一个像素的范围会被海水淹没。具体来说如果一块陆地像素与海洋相邻（上下左右四个相邻像素中有海洋），它就会被淹没。

例如上图中的海域未来会变成如下样子：

.......
.......
.......
.......
....#..
.......
.......

请你计算：依照科学家的预测，照片中有多少岛屿会被完全淹没。

输入格式

第一行包含一个整数 $N$ 。 $\le N \le 1000)$ 。

以下 $N$ 行 $N$ 列代表一张海域照片。

照片保证第 $1$ 行、第 $1$ 列、第 $N$ 行、第 $N$ 列的像素都是海洋。

输出格式

一个整数表示答案。

样例输入 #1

7 
.......
.##....
.##....
....##.
..####.
...###.
.......

样例输出 #1

提示

时限 1 秒, 256M。蓝桥杯 2018 年第九届省赛

思路

我一开始思考的时候能想到深搜，但是一直纠结于题目的意思：其中 "上下左右" 四个方向上连在一起的一片陆地组成一座岛屿，想着搜到2行n列，或者n行2列的就是会被淹没的。但是这样不知道怎么实现
看了别人的题解，发现大致都是一个思路：看岛屿会被淹没的#是否等于岛屿总#数判断是否会被淹没

题解

#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
char g[N][N];
bool st[N][N];
int n;
int total, brink;
const int dx[] = {-1,0,1,0}, dy[] = {0,1,0,-1};
void dfs(int x,int y) {
    st[x][y] = true;
    total ++;
    for(int i = 0;i < 4;i ++)
        if(g[x + dx[i]][y + dy[i]] == '.') {
            brink ++;
            break;
        } 
    for(int i = 0;i < 4;i ++) {
        int tx = x + dx[i], ty = y + dy[i];
        if(tx < 0 || tx >= n || ty < 0 || ty >= n) continue;
        if(g[tx][ty] == '#' && !st[tx][ty]) {
            dfs(tx,ty);
        }
    }
}
int main(){
    cin >> n;
    for(int i = 0;i < n;i ++) cin >> g[i];
    int cnt = 0;
    for(int i = 0;i < n;i ++)
        for(int j = 0;j < n;j ++)
            if(g[i][j] == '#' && !st[i][j]) {
                total = brink = 0;
                dfs(i,j);
                if(total == brink) cnt ++;
            }
    cout << cnt << endl;
}

[蓝桥杯 2018 省 A] 小朋友崇拜圈

班里 $N$ 个小朋友，每个人都有自己最崇拜的一个小朋友（也可以是自己）。

在一个游戏中，需要小朋友坐一个圈，每个小朋友都有自己最崇拜的小朋友在他的右手边。

求满足条件的圈最大多少人？

小朋友编号为 $1, 2, 3, \dots N$ 。

输入描述
输入第一行，一个整数 $N（3<N<10^5 ）$ 。

接下来一行 $N$ 个整数，由空格分开。

输出描述
要求输出一个整数，表示满足条件的最大圈的人数。

样例输入 #1

9
3 4 2 5 3 8 4 6 9

样例输出 #1

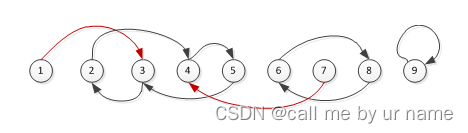
说明
如下图所示，崇拜关系用箭头表示，红色表示不在圈中。

显然，最大圈是[2 4 5 3] 构成的圈。

在这里插入图片描述

运行限制

最大运行时间：1s
最大运行内存: 256M

思路

我写这道题能想到是用深搜写：遍历每一个数字，对每个数字依据他的喜好关系进行深搜。用一维数组存储一开始输入的喜好关系，用一个pair<int,int>来存储是否经过和在深搜路的第几个位置。当遇到深搜遇到走过的序号时就是形成了一个圈的时候，就用当前数所在深搜路的位置减去它喜好的点的位置。但是没有想到优化方法，时间复杂度大概是 $O(n^2)$

题解

#include <iostream>
using namespace std;
const int MAXN=100001;
int worship[MAXN];
bool visit[MAXN];
int n,ans;
void dfs(int k,int step,int goal){
  if(visit[k]&&k!=goal) return;
  if(visit[k]&&k==goal){
    if(step>ans) ans=step;
    return; 
  }
  visit[k]=true;
  int next=worship[k];
  dfs(next,step+1,goal);
  visit[k]=false;
}
int main(){
  cin>>n;
  for(int i=1;i<=n;++i) cin>>worship[i];
  for(int i=1;i<=n;++i){
    visit[i]=true;
    dfs(worship[i],1,i);
  }
  cout<<ans;
}

幸运数字Ⅱ

题目描述

定义一个数字为幸运数字当且仅当它的所有数位都是4或者7。
比如说，47、744、4都是幸运数字而5、17、467都不是。
定义next(x)为大于等于x的第一个幸运数字。给定l，r，请求出next(l) + next(l + 1) + … + next(r - 1) + next(r）

输入描述

两个整数l和r (1 <= l <= r <= 1000,000,000)。

输出描述

一个数字表示答案

示例一
输入

2 7

输出

33

示例二
输入

7 7

输出

7

首先描述一下，我一开始写的想法：对 l--r 上的每一个数用一遍搜索，然后搜索到一个 “幸运数字” ，然后再剪枝（没写上去）。但是开销是：需要对 l--r 及 r 后面一定数量的数字，统统进行check的遍历（当数字位数长的时候，遍历数字string的开销大）

思路

将0到最大值的数中所有的 “幸运数字” 找出来（通过n*10，降低时间开销到9位数）
sort一下 “幸运数字” 的数组，将其按从小到大排序，然后辅助后面的剪枝策略

题解

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll a[1001000];
ll cnt =0;
void dfs(ll n){
    if(n>=44444444444) return;
    a[cnt++]=n*10+4;
    a[cnt++]=n*10+7;
    dfs(n*10+4),dfs(n*10+7);
}
int main(){
    ll l,r,pos=0,ans=0;
    cin>>l>>r;
    dfs(0);
    sort(a,a+cnt);
    for(ll i=l;i<=r;i++){
        while(a[pos]<i) pos++;
        ans+=a[pos];
    }
    cout<<ans;
}

下面的题是含有剪枝策略的深搜题

[NOI1999]生日蛋糕

题目描述

输入描述

有两行，第一行为N(N≤10000)，表示待制作的蛋糕的体积为Nπ；第二行为M(M≤20)，表示蛋糕的层数为M。

输出描述

仅一行，是一个正整数S（若无解则S=0）。

示例一
输入

100
2

输出

68

备注

附：圆柱公式
体积V=πR2H
侧面积A’=2πRH
底面积A=πR2

思路

看到题目，首先可能会想到贪心（因为题目中提到了最，但是很明显，每一步会影响到后面的操作，所以摒弃）
当然，不难想到用dfs算法，并且一定要剪枝（因为普通深搜，光想想时间复杂度都极高）
接着确定剪枝条件（这道题说真的，还是挺考察数学知识的，在理解数学关系的一些地方卡了很久🥗🥗🥗）：
1. 在中途dfs中计算出的 面积>已知最小面积
2. 在中途dfs中计算出的 体积>题目给出的体积
3. 在中途dfs中 估算出的最小体积>已知最小体积 别问我怎么想到这3个，一遍一遍地TLE，慢慢迭代出来的
设计dfs算法：
1. 首先确定return条件，如果搜到最高层时并且体积=题目给出的体积就取一下最小体积并return
2. 开始遍历：我的题解是从蛋糕下往上搜。先从半径开始（可能从高开始也行），半径的范围需要确定最小为层数，最大为该层的下方那层的半径-1，，高度范围高度最小为该层层数，最大应该由给出的体积，已知体积和假设的最小体积估算
3. 大体上就没了，具体细节在代码里解释

题解

#include<bits/stdc++.h>
using namespace std;
int mins[25],minv[25],n,m,ans=INT_MAX;         //mins和minv存放估计的最小面积和体积（因为题目中说明了半径和高度为整数，并且由上往下递增，所以可以估计最小）
void dfs(int dep,int r,int h,int s,int v){   //传入的dep是要计算的那层层数，而r,h是上一层的半径和高度
    if(dep==0){
        if(v==n) ans=min(ans,s);
        return;
    }
    int max_height=h;
    if(s+mins[dep-1]>=ans) return;
    if(v+minv[dep-1]>n) return;
    if(2*(n-v)/r+s>=ans) return;
    for(int i=r-1;i>=dep;--i){
        if(dep==m) s=i*i;
        max_height=min(h-1,(n-minv[dep-1])/i/i);  //这里是确定高度的上界，n-minv[]……得到的是由估算最小体积计算出的高度。因为h-1是当前层数不可逾越的最大高度，而n-minv……同样也是不可逾越的最大高度，所以取两个中较小那个
        for(int j=max_height;j>=dep;--j) dfs(dep-1,i,j,s+2*i*j,v+i*i*j);
    }
}
int main(){
    scanf("%d%d",&n,&m);
    memset(mins,0,sizeof(mins));
    memset(minv,0,sizeof(minv));
    for(int i=1;i<=m;++i) mins[i]=mins[i-1]+2*i*i,minv[i]=minv[i-1]+i*i*i;
    dfs(m,n,n,0,0);
    if(ans==INT_MAX) printf("-1");
    else printf("%d",ans);
}