Reinforcement Learning for Reasoning in Large Language Models with One Training Example论文解读

abstract

单样本可验证奖励强化学习提升大语言模型数学推理能力的研究

我们研究表明，使用单个训练样本的可验证奖励强化学习（1-shot RLVR）能有效激发大语言模型（LLMs）的数学推理能力。将RLVR应用于基础模型Qwen2.5-Math-1.5B后，我们发现单个样本即可将模型在MATH500基准上的性能从36.0%提升至73.6%，并将其在六个常见数学推理基准上的平均性能从17.6%提升至35.7%。这一结果与使用包含上述样本的1200个样本的DeepScaleR子集（MATH500：73.6%，平均：35.9%）所获得的性能持平。此外，仅使用两个样本的RLVR甚至能略微超越上述结果（MATH500：74.8%，平均：36.6%）。

在不同模型（Qwen2.5-Math-7B、Llama3.2-3B-Instruct、DeepSeek-R1-Distill-Qwen-1.5B）、不同强化学习算法（GRPO和PPO）以及不同数学样本（其中许多样本作为单个训练样本使用时，能使模型在MATH500上的性能提升约30%或更高）上，均观察到了类似的显著提升。

此外，我们在1-shot RLVR训练过程中发现了一些有趣的现象，包括跨领域泛化、自我反思频率提高，以及即使训练准确率达到饱和后，测试性能仍能持续提升（我们将这一现象称为“饱和后泛化”）。同时，我们证实1-shot RLVR的有效性主要源于策略梯度损失，这使其有别于“顿悟（grokking）”现象。我们还发现，在1-shot RLVR训练中，促进模型探索（例如通过引入具有适当系数的熵损失）起着关键作用。

值得一提的是，我们观察到即使不使用任何结果奖励，仅应用熵损失，也能使Qwen2.5-Math-1.5B在MATH500上的性能提升27.4%。我们还进一步讨论了与格式修正、标签鲁棒性和提示修改相关的观察结果。

这些发现可为未来RLVR数据效率相关研究提供启发，并促使人们重新审视RLVR领域的最新进展及其潜在机制。我们的代码、模型和数据已开源，地址为：https://github.com/ypwang61/One-Shot-RLVR。

1 Introduction

该论文的Introduction部分围绕大语言模型（LLMs）推理能力优化的技术背景、现有研究缺口及核心研究方向展开，具体内容如下：

1. LLM推理能力提升的研究现状

近年来，LLMs在推理能力（尤其是复杂数学任务）上取得显著进展，典型代表包括OpenAI-o1、DeepSeek-R1、Kimi-1.5等模型。其中，可验证奖励强化学习（RLVR） 是推动这一进展的关键方法——它通过基于规则的结果奖励（如数学问题答案正确性的二元奖励）对LLM进行强化学习，已被证实能激发模型的特定认知行为（如自我反思）并提升跨下游任务的泛化能力。

当前研究多聚焦于RL算法优化，例如通过改进PPO、GRPO等算法以提升RLVR的性能与稳定性，但在数据中心视角（data-centric aspects） 的探索相对不足：尽管已有研究尝试构建高质量数学推理数据集（如相关文献[17,18,11]），但对“RLVR中数据的具体作用”缺乏深入挖掘，核心问题仍未解决，例如“RLVR真正需要多少数据？”“哪些数据最有效？”“训练数据的质量与数量如何影响自我反思、稳健泛化等实证现象？”。

文中提及与该方向最相关的研究是LIMR，其提出“学习影响度量（LIM）”指标评估训练样本有效性，能在缩减6倍训练样本的同时维持模型性能，但该研究未探索RLVR训练数据集的极致缩减边界。

2. 核心研究问题与初步发现

基于上述研究缺口，论文明确核心研究问题：在维持与全量数据集相近性能的前提下，RLVR训练数据集能缩减到何种程度？

通过实证研究，论文初步揭示了关键发现：RLVR训练数据集可极致缩减至单个样本（1-shot RLVR） 。这一发现不仅支持了“基础模型本身已具备显著推理能力”的近期观点（相关文献[13,20,6,21]），还进一步证明“单个样本足以大幅提升基础模型的数学性能”。

3. 研究贡献与发现概述

Introduction部分还简要概括了论文的核心贡献与关键发现，为后续章节铺垫：

• 单样本性能媲美全量数据：筛选出的单个样本（如${\pi }_1$）用于1-shot RLVR时，能使Qwen2.5-Math-1.5B模型在MATH500上的性能从36.0%提升至73.6%，在6个数学推理基准上的平均性能从17.6%提升至35.7%，与包含该样本的1209个样本的DeepScaleR子集（DSR-sub）训练效果几乎持平；且这些有效单样本对基础模型而言难度较低，无需训练即可高概率解决。
• 跨模型/算法有效性：1-shot/few-shot RLVR在不同基础模型（Qwen2.5-Math-1.5B/7B、Llama3.2-3B-Instruct）、基于长思维链（CoT）数据蒸馏的模型（DeepSeek-R1-Distill-Qwen-1.5B），以及不同RL算法（GRPO、PPO）上均有效。
• 独特实证现象：1-shot RLVR存在“饱和后泛化（post-saturation generalization）”——训练准确率快速趋近100%后，测试准确率仍持续提升，且过拟合出现极晚（约1400步后），过拟合后测试性能仍稳健、推理输出仍可解释；此外，1-shot RLVR还能实现跨领域泛化（如基于几何样本训练提升代数、数论领域性能），并增加模型在下游任务中自我反思的频率。
• 机制与关键组件：通过消融实验证实，1-shot RLVR的有效性主要源于策略梯度损失，与依赖权重衰减等正则化的“顿悟（grokking）”现象有本质区别；同时，促进模型探索（如引入适当系数的熵损失）至关重要，甚至仅用熵损失（无结果奖励）就能使Qwen2.5-Math-1.5B在MATH500上性能提升27%。此外，还讨论了格式修正、标签鲁棒性、提示修改等相关观察结果。

2 Preliminary

该部分主要围绕RLVR训练的核心损失函数与数据选择方法展开，为后续实验设计提供理论与方法基础，具体内容如下：

1. RL损失函数（基于GRPO算法）

论文默认采用GRPO（Generalized Proximal Policy Optimization）作为LLM的RL算法，明确其损失函数包含三大核心组件，并补充了各组件的作用与计算逻辑（详细公式推导见附录B.1）：

• （1）策略梯度损失（Policy Gradient Loss）
  核心作用是“强化高奖励输出、惩罚低奖励输出”：根据“组归一化优势（group-normalized advantages）”为模型输出分配权重，使优于平均水平的解决方案（如数学问题的正确答案）得到强化，劣于平均水平的方案被抑制。
  针对数学任务，奖励定义为0-1二元奖励：仅当模型输出的最终答案与真实标签完全匹配时，奖励为1；否则为0。论文暂未纳入格式奖励，相关讨论放在附录C.2.3中。

• （2）KL散度损失（KL Divergence Loss）
  用于“维持模型的通用语言生成质量”：通过衡量当前模型与参考模型（reference model）输出分布的差异，避免模型在强化学习过程中过度偏离原始语言能力，确保生成内容的流畅性与合理性。

• （3）熵损失（Entropy Loss）
  作用是“促进模型探索多样化推理路径”：通过负系数（默认$\alpha =-0.001$）激励模型输出更高的“逐token熵（per-token entropy）”，增加推理过程的多样性。
  论文特别指出，熵损失并非GRPO训练的必需组件，但因实验采用的verl框架（文献[22]）默认包含该组件而保留；其对1-shot RLVR的具体影响在后续4.1节进一步分析。

2. 数据选择方法：历史方差评分（Historical Variance Score）

为探索RLVR训练数据集的极致缩减边界，论文提出一种简单且可复现的数据选择策略，用于筛选高效的单样本/few样本，具体步骤如下：

• 步骤1：计算历史训练准确率方差
  先使用全量数据集对模型进行E轮RLVR训练，记录每个样本$i$在每一轮的平均训练准确率，形成准确率序列$L_i=[s_{i,1},s_{i,2},...,s_{i,E}]$。
  基于文献[23]中“奖励信号的方差对RL训练至关重要”的结论，计算每个样本准确率序列的方差$v_i=var(s_{i,1},...,s_{i,E})$（公式1），方差越大，代表该样本在训练中奖励信号的波动越显著，理论上对模型的训练指导作用更强。

• 步骤2：样本排序与筛选
  对所有样本按方差降序排序，得到排列$\pi :[N]\to [N]$（$N$为全量样本总数），其中${\pi }_j$（简写为${\pi }_j$）代表方差排名第$j$的样本（公式2）。
  实验中，基于Qwen2.5-Math-1.5B的历史方差评分筛选出的${\pi }_1$（方差最大样本）在1-shot RLVR中表现优异（见3.2.3、3.3节）；同时从${\pi }_1$至${\pi }_{17}$中选择不同领域的样本进一步验证，发现${\pi }_{13}$同样具备高效性。
  论文强调，该排序标准并非“1-shot RLVR样本选择的最优解”——附录Tab.3显示，即使是方差中等或较低的样本，单独作为训练样本时，也能使MATH500性能提升约30%或更高，说明1-shot RLVR的有效性可能是一种不依赖特定选择方法的通用现象。

3 Experiments

3.1 Setup

该部分详细阐述了实验的核心配置，涵盖模型选择、数据集设计、训练参数、评估基准与方法，为后续实验的可复现性与结果可信度提供支撑，具体内容如下：

1. 模型（Models）

实验默认以Qwen2.5-Math-1.5B为核心测试模型，同时为验证1-shot/few-shot RLVR的通用性，进一步在以下模型上开展实验（详细结果见3.3节）：

• Qwen2.5-Math-7B（同系列更大参数量数学模型）；
• Llama-3.2-3B-Instruct（Meta推出的指令微调模型）；
• DeepSeek-R1-Distill-Qwen-1.5B（基于长思维链（CoT）数据蒸馏得到的模型）；
• 附录C.1.2中还补充了Qwen2.5-1.5B（基础通用模型）与Qwen2.5-Math-1.5B-Instruct（指令微调版本数学模型）的实验结果。

2. 数据集（Dataset）

实验围绕“数据量缩减”核心目标设计数据集，主要包含以下几类：

（1）核心样本池：DSR-sub

• 来源：从DeepScaleR-Preview-Dataset中随机抽取1209个数学问题-答案对，作为数据选择与1-shot/few-shot RLVR的基础样本池，简称“DSR-sub”；
• 数据选择依据：先让Qwen2.5-Math-1.5B在DSR-sub上训练500步，基于2.2节提出的“历史方差评分”计算每个样本的准确率方差并排序，得到固定的样本序列{π1,π2,...,π1209}\{\pi_1,\pi_2,...,\pi_{1209}\}{π1​,π2​,...,π1209​}（后续所有实验均沿用此排序，确保一致性）。

（2）对比数据集：MATH

• 来源：采用MATH数据集的训练集（含7500个数学竞赛题），用于与DSR-sub的全量训练结果对比，验证数据量缩减的有效性。

（3）1-shot/few-shot数据集构建

• 方法：将选中的1个或少数几个样本（如${\pi }_1$、${\pi }_{13}$）重复复制，直至达到训练批次大小（实验中为128），生成独立的1-shot/few-shot训练数据集；
• 目的：模拟“极致数据量缩减”场景，避免批次大小不匹配影响训练稳定性。

3. 训练配置（Training）

训练流程基于verl框架实现，关键参数与设置如下：

• 损失函数系数：默认KL散度损失系数$\beta =0.001$，熵损失系数$\alpha =-0.001$（与2.1节GRPO损失函数定义一致）；
• 生成参数：训练rollout温度设为0.6（基于vLLM框架实现高效生成）；
• 批次与更新策略：训练批次大小与 mini-batch 大小均为128，每个prompt采样8个响应，对应8次梯度更新；
• 上下文长度：考虑到Qwen2.5-Math-1.5B/7B的上下文长度为4096，设置最大提示长度1024、最大响应长度3072；
• 更多细节（如学习率、权重衰减系数）见附录B.4。

4. 评估配置（Evaluation）

（1）评估框架与基准

• 评估管道：采用Qwen2.5-Math官方评估 pipeline，确保与主流数学模型评估标准一致；
• 核心数学基准：6个复杂数学推理基准，包括MATH500（500个精选数学题）、AIME 2024/2025（各30题）、AMC 2023（40题）、Minerva Math（272道本科STEM题）、OlympiadBench（675道奥林匹克级数学题）；
• 非数学基准：补充ARC-Easy（5197道简单科学推理题）与ARC-Challenge（2590道复杂科学推理题），验证跨领域泛化能力（结果见Tab.1）。

（2）评估参数与稳定性保障

• 小样本基准处理：AIME 2024/2025、AMC 2023因题目数量少（30-40题），重复测试8次以确保稳定性，最终报告平均pass01（avg@8）性能；
• 温度参数：除上述小样本基准外，其他数学基准的评估温度设为0，减少随机性影响；
• 生成长度与模板：默认最大生成token数3072，Qwen系列模型使用“qwen25-math-cot”提示模板，Llama与蒸馏模型使用各自原生对话模板；
• 更多细节（如评估设备、种子设置）见附录B.5。

3.2 Observation of 1/Few-Shot RLVR

3.2.1 单样本拆解：${\pi }_1$是难度较低的问题

论文首先聚焦核心单样本${\pi }_1$（基于历史方差评分筛选的最优样本之一），揭示其特性与基础模型对它的初始处理能力：

• ${\pi }_1$的问题本质：${\pi }_1$是一道带有物理背景的简单代数题，核心步骤为根据“风力压强$P$与帆面积$A$、风速$V$的三次方成正比（$P=kA{V}^3$）”的关系，先计算比例系数$k=1/256$，再求解$V=\sqrt[3]{2048}$；且其标注答案“12.8”并非精确值（精确值约为12.699，即$\sqrt[3]{2048}\approx 12.7$）。
• 基础模型的初始能力：无需任何训练，Qwen2.5-Math-1.5B已能高概率解决${\pi }_1$的核心步骤——仅在计算$\sqrt[3]{2048}$时输出多样（如4、10.95、12.699、12.7、12.8、13等）。对基础模型128次采样的统计显示，57.8%的输出为“12.7”或“12.70”，6.3%为标注答案“12.8”，6.3%为“13”，说明该样本对基础模型而言难度较低，1-shot RLVR的作用并非“教会模型解决新问题”，而是“激发其已有推理能力的稳定性”。
• 附录C.2.5还补充了“简化版${\pi }_1$（仅保留$\sqrt[3]{2048}$计算步骤）”的实验，进一步验证问题复杂度对1-shot RLVR效果的影响。

3.2.2 饱和后泛化：训练准确率饱和后测试性能仍持续提升

这是1-shot RLVR中最关键的现象，论文通过训练与测试曲线对比（Fig.2）及输出内容分析（Fig.3），详细阐述其特性：

图2：单样本可验证奖励强化学习（1-shot RLVR）中的饱和后泛化现象。使用样本${\pi }_1$（左图）和${\pi }_{13}$（中图）进行RLVR训练时，模型的训练准确率在100步之前就达到饱和，但测试性能仍持续提升。与之相对，使用1200个样本的DSR-sub数据集（右图）进行RLVR训练时，模型的训练准确率在2000步之后仍未饱和，然而在1000步之后，测试任务的性能已无显著提升。

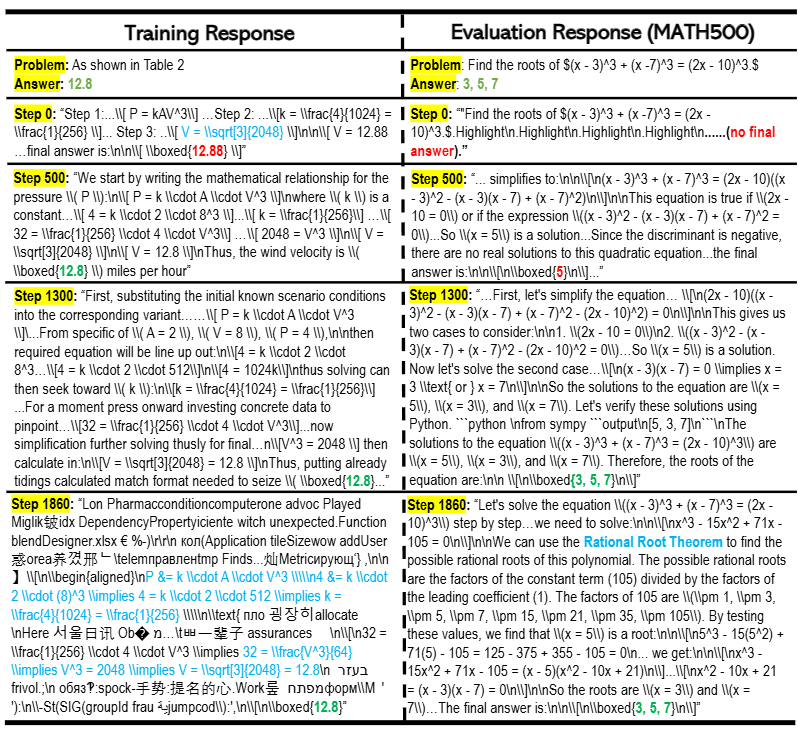
图3：在单样本可验证奖励强化学习（1-shot RLVR）的饱和后泛化现象中，即便模型对训练样本发生过拟合，仍能在测试数据上实现泛化。本图展示了模型对训练样本${\pi }_1$和一道选定的MATH500题目所生成的响应，其中绿色/红色分别用于标记正确/错误答案。
模型在500步之前就已在${\pi }_1$上收敛，随后（1300步时）尝试以不同风格为${\pi }_1$生成更长的解题过程，且在评估任务上的表现逐步提升。但在1860步时（此时模型在MATH500上的准确率达到74%），模型对训练样本${\pi }_1$出现明显过拟合——其输出将正确解题过程（青色标注）与无意义内容混杂在一起。尽管如此，模型对测试题目的响应仍保持正常，甚至尝试了与1300步时不同的解题策略（“有理根定理”）。

• 现象表现：由于仅使用单个样本训练，模型对${\pi }_1$或${\pi }_{13}$的训练准确率会快速饱和（如${\pi }_1$在100步前趋近100%），但测试性能仍持续提升——${\pi }_1$从100步到1540步，在6个数学基准上的平均性能提升3.4%；${\pi }_{13}$从500步到2000步，平均性能提升9.9%。而全量数据集（DSR-sub）的RLVR训练中，测试性能在训练准确率收敛前就已开始下降，无法观察到该现象。
• 过拟合的特殊性：1-shot RLVR的过拟合出现极晚（${\pi }_1$约1400步后，${\pi }_{13}$约1800步后），且过拟合后仍维持测试性能：过拟合阶段，模型对训练样本${\pi }_1$的输出会混合正确计算过程与无意义的多语言乱码，但对测试样本的推理输出仍清晰、符合人类可解释性，且准确率保持高位（如${\pi }_1$过拟合后MATH500准确率仍达74%）。这一现象被定义为“post-saturation generalization（饱和后泛化）”，凸显1-shot RLVR在泛化能力上的独特优势。

3.2.3 1-shot RLVR对多样本有效且实现跨领域泛化

论文通过筛选不同方差、不同领域的样本（高方差${\pi }_1-{\pi }_{17}$、中等方差${\pi }_{605}-{\pi }_{606}$、低方差${\pi }_{1201}-{\pi }_{1209}$）开展实验，验证1-shot RLVR的普适性与跨领域能力：

• 多样本有效性：几乎所有样本单独用于1-shot RLVR时，均能使MATH500性能提升≥30%，仅${\pi }_{1207}$（标签错误）与${\pi }_{1208}$（问题过难，模型难获奖励）的提升幅度较低（分别为18.0%、9.0%）。部分提升源于“格式修正”（如模型输出更规范的\boxed{}​包裹答案，附录C.2.3详细讨论），但优质样本（如${\pi }_1$）能在格式修正之外，带来额外的推理能力提升。
• 跨领域泛化能力：1-shot RLVR训练不局限于提升“训练样本所属领域”的性能，而是能迁移至其他领域。例如，用几何领域的${\pi }_{13}$训练，模型在代数、数论领域的性能也显著提升；数论领域的${\pi }_{11}$训练后，其在数论领域的提升反而低于用预微积分领域${\pi }_{605}$训练的效果。这表明1-shot RLVR激发的是模型通用推理能力，而非领域特定知识，与“模型推理能力无法通过表面领域特征预测”的观点（文献[35]）一致。

3.2.4 测试数据中自我反思行为更频繁

论文通过统计模型输出中“rethink”“recheck”“recalculate”等自我反思关键词的频率，发现1-shot RLVR能促进模型更复杂的推理行为：

• 自我反思的动态变化：基础模型本身已存在一定自我反思行为（支持近期“基础模型具备潜在推理能力”的研究结论），而1-shot RLVR训练后期（约1250步后），测试任务中含自我反思关键词的响应数量显著增加，且这一趋势与“训练样本响应长度增加”“熵损失上升”同步（Fig.4）——说明模型在探索更多样推理路径的同时，也更倾向于通过自我检查优化推理过程。
• 与全量RLVR的对比：使用1209个样本的DSR-sub训练时，随着训练推进，模型自我反思频率反而略有下降，且响应长度缩短，进一步凸显1-shot RLVR在激发模型主动推理行为上的优势。

4 Analysis

4.1 消融研究：策略梯度损失是核心贡献者，熵损失进一步提升饱和后泛化

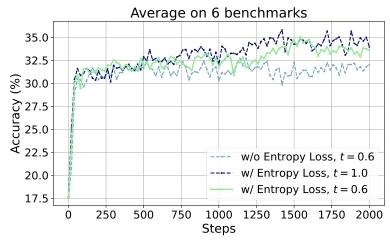
图 5：鼓励探索可提升饱和后泛化性能。其中，t 代表训练采样（training rollouts）的温度参数。

为明确RL损失函数各组件对1-shot RLVR有效性的贡献，并区分其与“grokking（顿悟）”现象的差异，论文开展了针对性消融实验（结果见Tab.5，测试曲线见附录C.2.1），核心结论如下：

• 策略梯度损失是性能提升的主要驱动：仅添加策略梯度损失（无权重衰减、KL散度损失、熵损失）时，Qwen2.5-Math-1.5B在MATH500上的性能已从36.0%提升至71.8%，AIME 2024从6.7%提升至15.4%，接近“全损失（策略梯度+权重衰减+KL散度+熵损失）”的效果（MATH500：74.8%，AIME 2024：17.5%）。这表明1-shot RLVR的有效性主要源于策略梯度损失对“正确答案的强化与错误答案的惩罚”。
• 与grokking现象的本质区别：grokking现象高度依赖权重衰减等正则化方法，而实验显示，在策略梯度损失基础上添加权重衰减（性能：MATH500 71.4%，AIME 2024 16.3%）或KL散度损失（性能：MATH500 70.8%，AIME 2024 15.0%），对模型性能无显著提升；反之，仅添加权重衰减与KL散度损失（无策略梯度损失）时，模型性能几乎无改善（MATH500 39.0%，AIME 2024 10.0%），进一步证明1-shot RLVR与grokking机制无关。
• 熵损失促进饱和后泛化：在全损失中加入熵损失（默认系数$\alpha =-0.001$），能使MATH500性能额外提升4.0%，AIME 2024提升2.5%；若熵损失系数过大（如$\alpha =-0.003$），则会导致训练不稳定，性能略有下降（MATH500 73.6%，AIME 2024 15.4%）。结合Fig.5的对比可知，无熵损失时，模型在训练准确率饱和（约150步）后，测试性能几乎不再提升；加入熵损失后，平均性能提升2.3%，若进一步提高训练rollout温度（$t=1.0$），可再获0.8%提升——说明熵损失通过“促进模型探索多样化推理路径”，对饱和后泛化现象至关重要。

4.2 仅熵损失训练与标签正确性分析

该部分进一步探索“无策略梯度损失时的性能变化”及“标签准确性对1-shot RLVR的影响”，补充了1-shot RLVR的鲁棒性与边界条件：

• 仅熵损失可独立带来性能提升：实验发现，即使移除策略梯度损失，仅保留熵损失（或同时保留权重衰减、KL散度损失），仍能提升模型性能。例如，仅用熵损失训练Qwen2.5-Math-1.5B时，MATH500性能从36.0%提升至63.4%（Tab.5 Row10）；类似现象也出现在Qwen2.5-Math-7B（MATH500从51.0%提升至57.2%）与Llama3.2-3B-Instruct（MATH500从40.8%提升至47.8%）上（Tab.6）。尽管这种提升幅度小于“策略梯度损失+熵损失”的组合，但证明熵损失可通过“增加输出多样性”独立激发模型部分推理能力。
• 标签正确性的影响：轻微误差可容忍，极端错误损害性能：论文通过修改${\pi }_1$的标签（原始标签为12.8，精确值为12.7）开展对比实验：
  1. 标签为精确值“12.7”时，性能与原始标签“12.8”接近（MATH500 73.4% vs 74.8%，AIME 2024 17.9% vs 17.5%），说明轻微标签误差不影响1-shot RLVR效果；
  2. 标签为模型可过拟合的错误值“4”时，性能显著下降（MATH500 57.0%，AIME 2024 9.2%），甚至低于“无策略梯度损失、仅熵损失”的情况；
  3. 标签为模型无法猜测与过拟合的极端错误值“9292725”时，性能（MATH500 64.4%，AIME 2024 9.6%）反而高于“标签为4”的情况，且接近“仅熵损失”的效果——说明模型在无法获取正确奖励信号时，会退化为依赖熵损失的探索行为。
• 全量数据集的标签鲁棒性延伸：附录C.2.4补充实验显示，若全量数据集（DSR-sub）中90%样本被分配随机错误标签，其RLVR性能（MATH500 67.8%）会低于1-shot RLVR（${\pi }_1$，MATH500 72.8%），说明RLVR对大规模标签噪声的容忍度有限，而优质单样本的稳定性更优。