二叉搜索树

1、概念

就是普通树的一种，然后具有其特殊的性质。

其左子树的所有值都小于根节点的值。

其右子树的所有值都大于根节点的值。

左右树都是二叉搜索树。

我们在这里直接利用一个数组进行创建一个搜索二叉树。

（7-2-4-6-3-1-5）  以8为根节点进行创建。

 

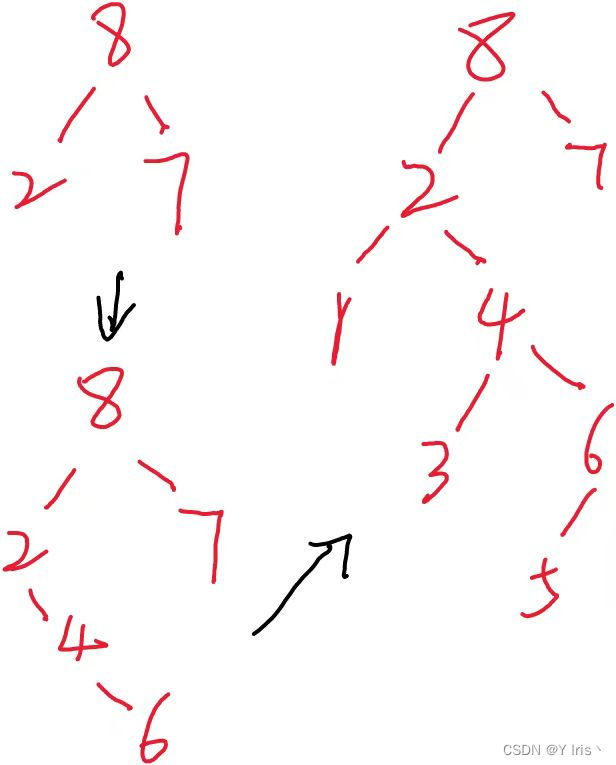
比根节点小的，就放在左边，比根节点大的，就放在右边，各位可以按照这个图了解一下。

2、增删查改的实现

我们首先要对树进行前期的准备，看代码。

	template<class T>
	struct BSTreeNode
	{
		typedef BSTreeNode<T> Node;//定义节点的属性

		Node* _left;
		Node* _right;
		T _key;

		BSTreeNode(const T& key)//节点初始化
			:_left(nullptr)
			, _right(nullptr)
			, _key(key)
		{}
	};

 

2.1、查找

这里的查找其实和二叉树差不多，但是这里实现应该是更简单一些，空就返回，小于查找值就去right，大于查找值就去left。但在这里我们用更简单的递归实现。

  bool _FindR(Node* root, const T& key)//找到就返回true，没有就返回false
{//利用递归实现
			if (root == nullptr)
				return false;

			if (root->_key < key)
			{
				return _FindR(root->_right, key);
			}
			else if (root->_key > key)
			{
				return _FindR(root->_left, key);
			}
			else
			{
				return true;
			}
}

2.2、增加—插入 

 这里其实也很好理解，就是找到通过递归找到正确位置后插入，然后将true返回给最初的函数。

bool _InsertR(Node*& root, const T& key)
		{
			if (root == nullptr)//找到正确位置后，直接将节点插入
			{
				root = new Node(key);
				return true;
			}

			if (root->_key < key)
			{
				return _InsertR(root->_right, key);
			}
			else if (root->_key > key)
			{
				return _InsertR(root->_left, key);
			}
			else
			{
				return false;
			}
		}

2.3、删除

这里的删除就很有讲究了， 详细解析在代码的注释里。

bool _EraseR(Node*& root, const T& key)
		{
			if (root == nullptr)
				return false;

			if (root->_key < key)
			{
				return _EraseR(root->_right, key);
			}
			else if (root->_key > key)
			{
				return _EraseR(root->_left, key);
			}
			else
			{
				Node* del = root;//此时找到我们要删除的节点
				if (root->_right == nullptr)//右边为空，那就把左边直接覆盖到此节点
				{
					root = root->_left;
				}
				else if (root->_left == nullptr)//反之，直接用右边的覆盖
				{
					root = root->_right;
				}
				else//左右节点都有孩子，特殊处理
				{
					Node* rightMin = root->_right;//我们这里利用右节点最小值（这里也可用左节点最大值，效果相同）来替代这个被删除的节点
//因为这两个值一定是大于被删除节点的左节点，小于右节点
					while (rightMin->_left)//找最左边的值
					{
						rightMin = rightMin->_left;
					}

					swap(root->_key, rightMin->_key);//直接交换

					return _EraseR(root->_right, key);//将交换后的值删除，也就是结尾的那个值
				}

				delete del;
				return true;
			}
		}

2.4、改 

这里的改就没有什么大的意义了，其实就复用一个查找的函数，然后直接替换那个被查找的数就可以了。 

  bool _replaceR(Node* root, const T& key，int x)//找到就返回true，没有就返回false
{//利用递归实现
			if (root == nullptr)
				return false;//修改失败，也就是没找到

			if (root->_key < key)
			{
				return _FindR(root->_right, key);
			}
			else if (root->_key > key)
			{
				return _FindR(root->_left, key);
			}
			else
			{
                root->_key=x;
				return true;//修改成功
			}
}