数据结构专题实验7——图的应用（景点管理）（C++实现）

一、实验概述

实验内容：应用图的技术，根据需求文件要求的功能，实现旅游景点的管理。实验要求：

1. 使用图的数据结构建立一个景点图的结构。
2. 可以查找各景点信息。
3. 旅游景点导航，使用深度优先，从一个景点开始遍历所有景点。
4. 查找一个景点到另一个景点的最短路径。
5. 对景点道路进行规划（使用最小生成树，使铺设的景点总道路长最短）。

二、代码结构

	旅游景点实际上就是无向图（有向图），这里利用无向图实现，运用了
一些经典的图的算法，例如：深度优先遍历、prim算法、最小生成树。而图也可
以抽象为一个矩阵。
	景点结构体vex，包括景点编号，景点名称，景点简介。
	边结构体edge，代表两个景点之间有道路（邻接矩阵）。

三、函数讲解

void Init()

	初始化Graph类，生成一个空的景点图（矩阵）。

void Graph::Init(){
    vexnum = 0;//初始化点的数量
    memset(matrix,0,sizeof(matrix));//初始化当前的图（点、边、权重）
    memset(vexs,0,sizeof(vexs));//初始化当前的点
}

bool InsertVex(Vex vex)

	添加点到vexs数组中。

bool Graph::InsertVex(Vex vex){
    if(vexnum!=SIZE){
    vexs[vexnum].num = vex.num;
    vexs[vexnum].name = vex.name;
    vexs[vexnum++].introduction = vex.introduction;
    }
    else
    return false;
    return true;
}

bool InsertEdge(Edge edge)

	将边edge的信息保存到邻接矩阵matrix中。

bool Graph::InsertEdge(Edge edge){
    for(int i = 0;i < vexnum;i++)
        for(int j = 0;j < vexnum;j++)
            if(i == edge.vex1 && j == edge.vex2){
                matrix[i][j] = edge.weight;
                return true;
            }
    return false;
}

Vex getVet(string name)

	查询点的信息。

Graph::Vex Graph::getVet(string name){
    for(int i = 0;i < vexnum;i++)
        if(name == vexs[i].name)
           return vexs[i];
}

int FindEdge(int nVex,Edge edges[])

	查询与一个点相连的边。

int Graph::FindEdge(int nVex,Edge edges[]){
    int index = 0;
    for(int j = 0;j < vexnum;j++)
        if(matrix[nVex][j]!=0){
            edges[index].vex1 = nVex;
            edges[index].vex2 = j;
            edges[index++].weight = matrix[nVex][j];
        }
    return index;
}

int getVexNum()

	得到当前点的个数。

int Graph::getVexNum(){
    return vexnum;
}

int FindShortPath(int start,int end,string &path)

	找到两点间最短路径。
	第一个嵌套for循环是为了将有向图变为无向图，大家可以根据自己的需要
修改，可以改在初始化时就变为无向图。
	distance数组存放最短道路的长度，path数组存放该道路经过景点的顺序
（道路本身）。
	通过佛洛依德算法来更新亮点间的最短路径，比如：A点到B点本身就有直达
的道路，此时distance数组会记录这个数字，但是A点到C点，C点到B点也有道
路，而且A->C->B这一道路长度小于A->B的道路长度，那么distance数组中A点
到B点的距离就会更新为这个更短的长度。所以在循环结束，每两个点之间的道
路都是最短的，因为每一次循环都在更新。
	sign2代表这条道路已经走完，不会继续循环。保证是在两个景点有通路的
前提下进行最小路径的比较。

int Graph::FindShortPath(int start,int end,string &path2){
    int distance[vexnum][vexnum];
    int tempMatrix[vexnum][vexnum];
    memset(tempMatrix,0,sizeof(tempMatrix));

    for(int i = 0;i < vexnum;i++)
        for(int j = 0;j < vexnum;j++)
            if(matrix[i][j]!=0 && matrix[j][i] == 0){
               tempMatrix[i][j] = matrix[i][j];
               tempMatrix[j][i] = matrix[i][j];
            }
    string path[vexnum][vexnum];
    //初始化路径矩阵
    for(int i = 0;i < vexnum;i++)
        for(int j = 0;j < vexnum;j++){
            distance[i][j] = tempMatrix[i][j];
            path[i][j] += to_string(j);
        }
    int sequence[7];
    memset(sequence,-1,sizeof (sequence));
    int sign2 = 0;
    for(int i = start;i < vexnum;i++)
        for(int j = 0;j < vexnum;j++)
              if(i != j)
                 for(int k = 0;k < vexnum;k++)
                    if(distance[i][j]!=0 && distance[j][k]!=0 && sign2 == 0){//&& sign1 == -1 && sign2 == 0
                        if((distance[i][k] > distance[i][j] + distance[j][k])||distance[i][k] == 0){
                            distance[i][k] = distance[i][j] + distance[j][k];
                            path[i][k] += to_string(j);
                            printf("i:%d j:%d k:%d",i,j,k);
                        }
                        if(k == end)
                            sign2 = -1;
                    }
        path2 = path[start][end] += to_string(start);
        cout << start << "->"  << end << ":" << path[start][end];
        printf(" shortestpath:%d ",distance[start][end]);
        printf(" path:%s ",path2.c_str());
        cout << endl;
        return distance[start][end];
}

void MST(Edge edges[])

	构造最小生成树。
	第一个嵌套for循环是为了将有向图变为无向图，大家可以根据自己的需要
修改，可以改在初始化时就变为无向图。
	INFINITY的值我给的是99999。我使用的是prim算法构造最小生成树，从第
一个景点开始，对其邻接的景点道路权重逐一进行比较，选取最小的那一个，
最近的道路会存到cloest数组中，该道路的权重会存到lowcost数组中。通过
一个嵌套for循环来更新最小权重，也能找到相应的最小道路。

void Graph::MST(Edge tree[]){
    int n = 0,min = INFINITY,tempMatrix[vexnum][vexnum],temp = 0;
    int cloest[vexnum],lowcost[vexnum];//closet为顶点i的最近邻点，lowcost存放（i,cloest[i]）的权值
    Edge e[vexnum-1];//从每个点出去的边
    memset(cloest,0,sizeof(cloest));
    memset(lowcost,0,sizeof(lowcost));
    memset(tempMatrix,0,sizeof(tempMatrix));

    for(int i = 0;i < vexnum;i++)
        for(int j = 0;j < vexnum;j++)
            if(matrix[i][j]!=0 && matrix[j][i] == 0){//
               tempMatrix[i][j] = matrix[i][j];
               tempMatrix[j][i] = matrix[i][j];
            }

    for(int i = 0;i < vexnum;i++){
        min = INFINITY;
        for(int j = 0;j < vexnum;j++){
            if(tempMatrix[i][j]!=0){
               temp = min;
               min = (min < tempMatrix[i][j])?min:tempMatrix[i][j];
               if(min != temp)
               cloest[i] = j;
            }
        }
        lowcost[i] = min;
    }

    cout << "MST: ";
    for(int i = 0;i < vexnum;i++){
        //cout << i << "——" << cloest[i] ;
        cout << "i: " << i << "  " << cloest[i] ;
    }

    cout << "  lowcost: ";
    for(int i = 0;i < vexnum;i++){
        //cout << i << "——" << cloest[i] ;
        cout << "i: " << i << "  " << lowcost[i] ;
    }
    for(int i = 0;i < vexnum;i++){
        tree[i].vex1 = i;
        tree[i].vex2 = cloest[i];
        tree[i].weight = lowcost[i];
    }
}

void DFS(int nVex,bool visited[],int sequence[],int &index)

	用深度优先搜索遍历图。
	第一个嵌套for循环是为了将有向图变为无向图，大家可以根据自己的需要
修改，可以改在初始化时就变为无向图。
	第二个嵌套for循环是利用邻接矩阵的特性，若有邻接的点，则满足if判断
条件。visited数组记录这个景点是否被遍历过了，sequence数组记录遍历的
顺序。然后在这个循环里递归调用DFS方法，直到visited数组中全都是true。
代表所有景点都已经遍历过了。

void Graph::DFS(int nVex,bool visited[],int sequence[],int &index){
    int tempMatrix[vexnum][vexnum];
    memset(tempMatrix,0,sizeof(tempMatrix));

    for(int i = 0;i < vexnum;i++)
        for(int j = 0;j < vexnum;j++)
            if(matrix[i][j]!=0 && matrix[j][i] == 0){
               tempMatrix[i][j] = matrix[i][j];
               tempMatrix[j][i] = matrix[i][j];
            }
    for(int i = 0;i < vexnum;i++)
       for(int j = 0;j  < vexnum;j++){
           if(tempMatrix[nVex][j]!=0 && !visited[j]){
              visited[j] = true;
              sequence[index++] = j;
              DFS(j,visited,sequence,index);
              printf("j:%d  ",j);
           }
       }
}

四、结果演示

	点击查看路线按钮，展示整个景点图。

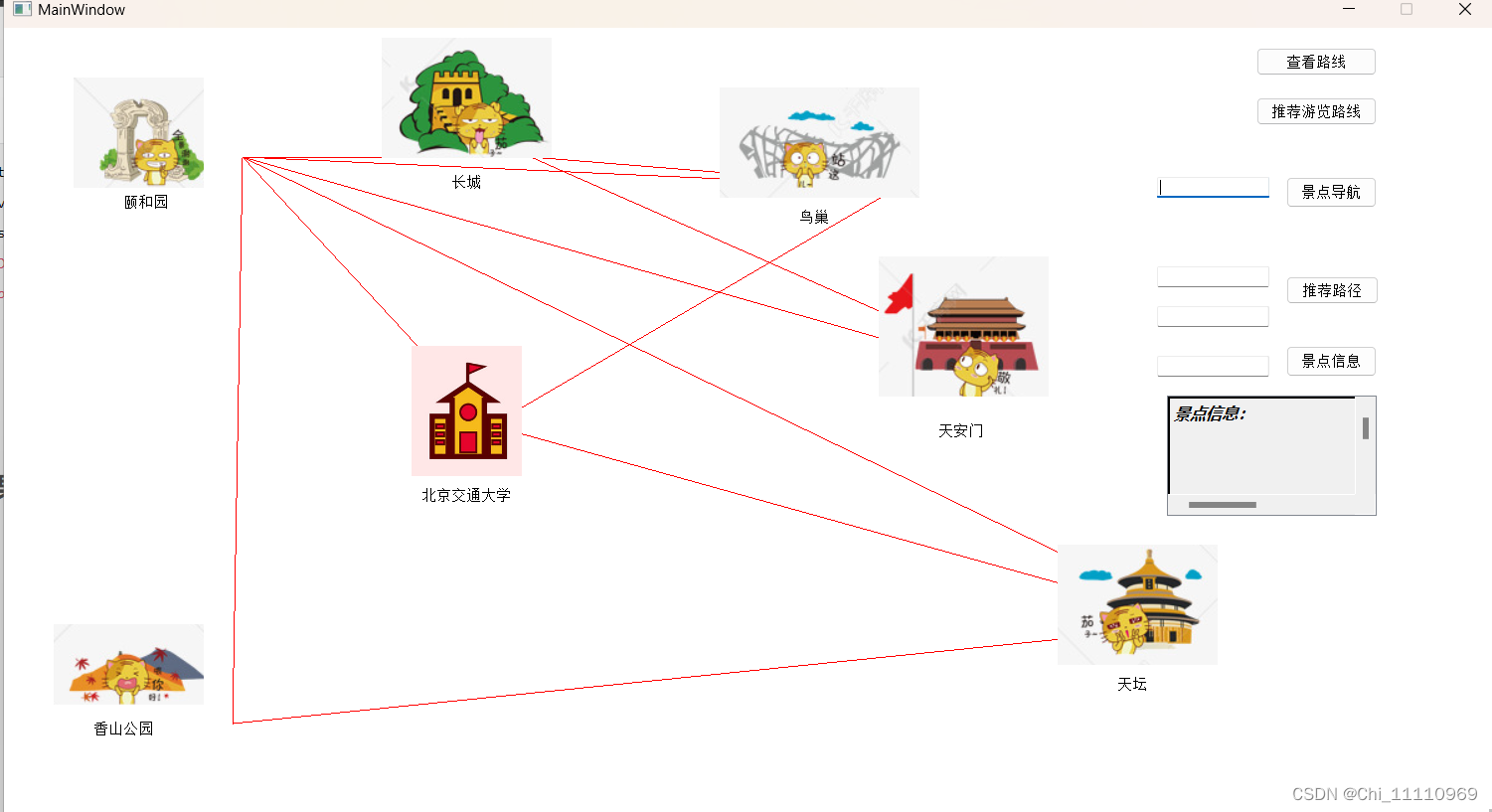
	点击推荐游览路线按钮，展示最小生成树。

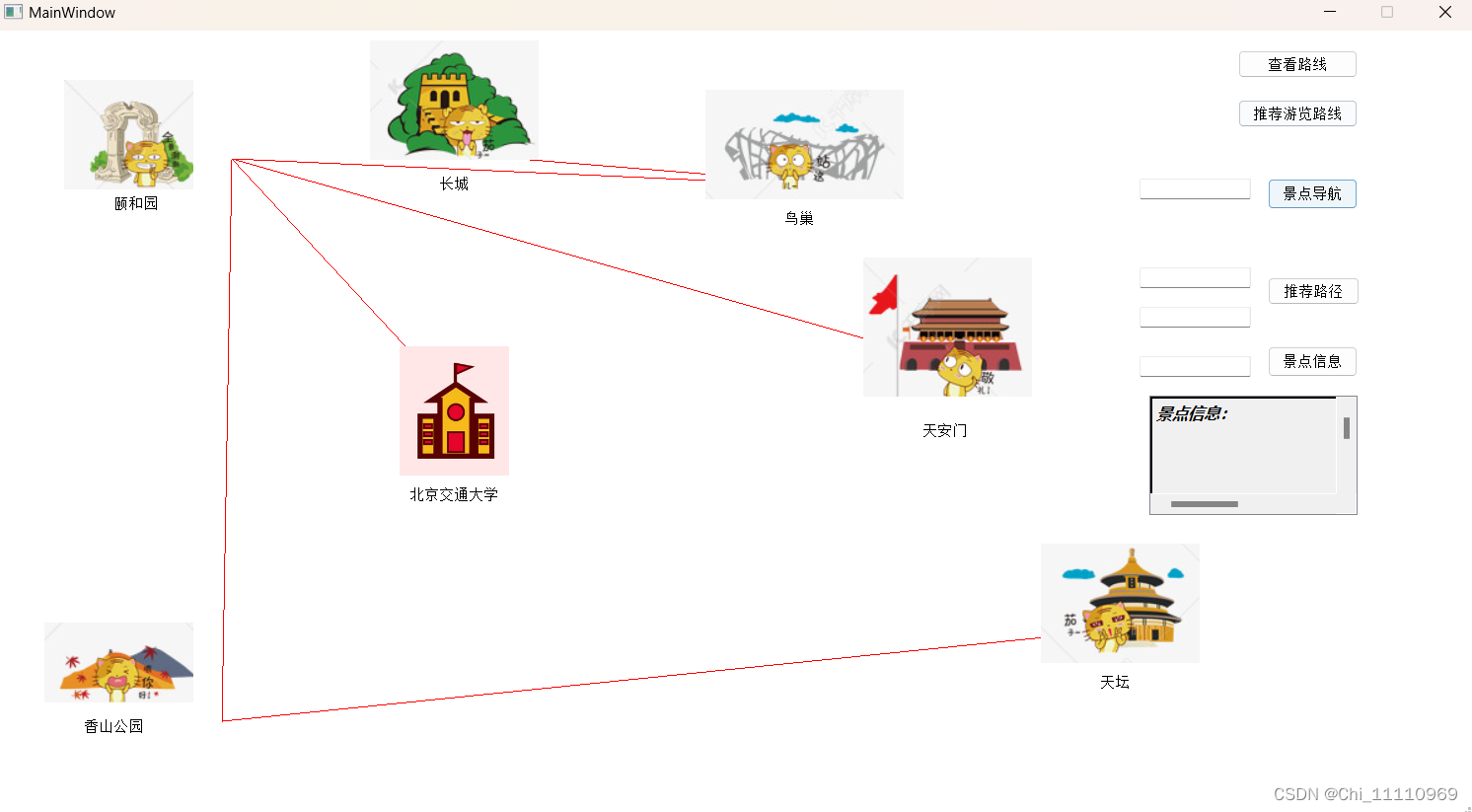
	输入一个景点名，点击景点导航，展示深度优先遍历结果。

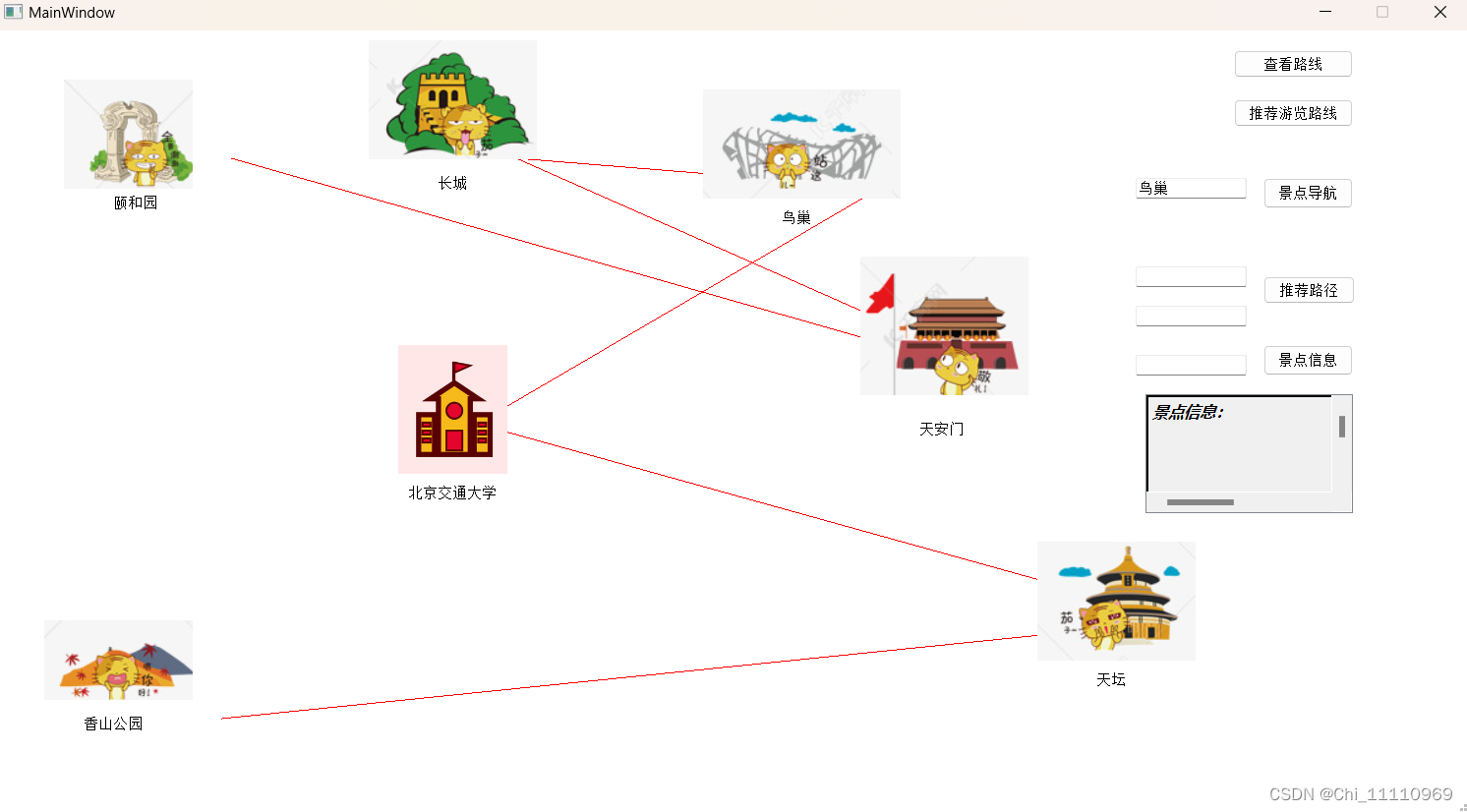
	输入两个景点名，点击推荐路线，寻找最短路径。

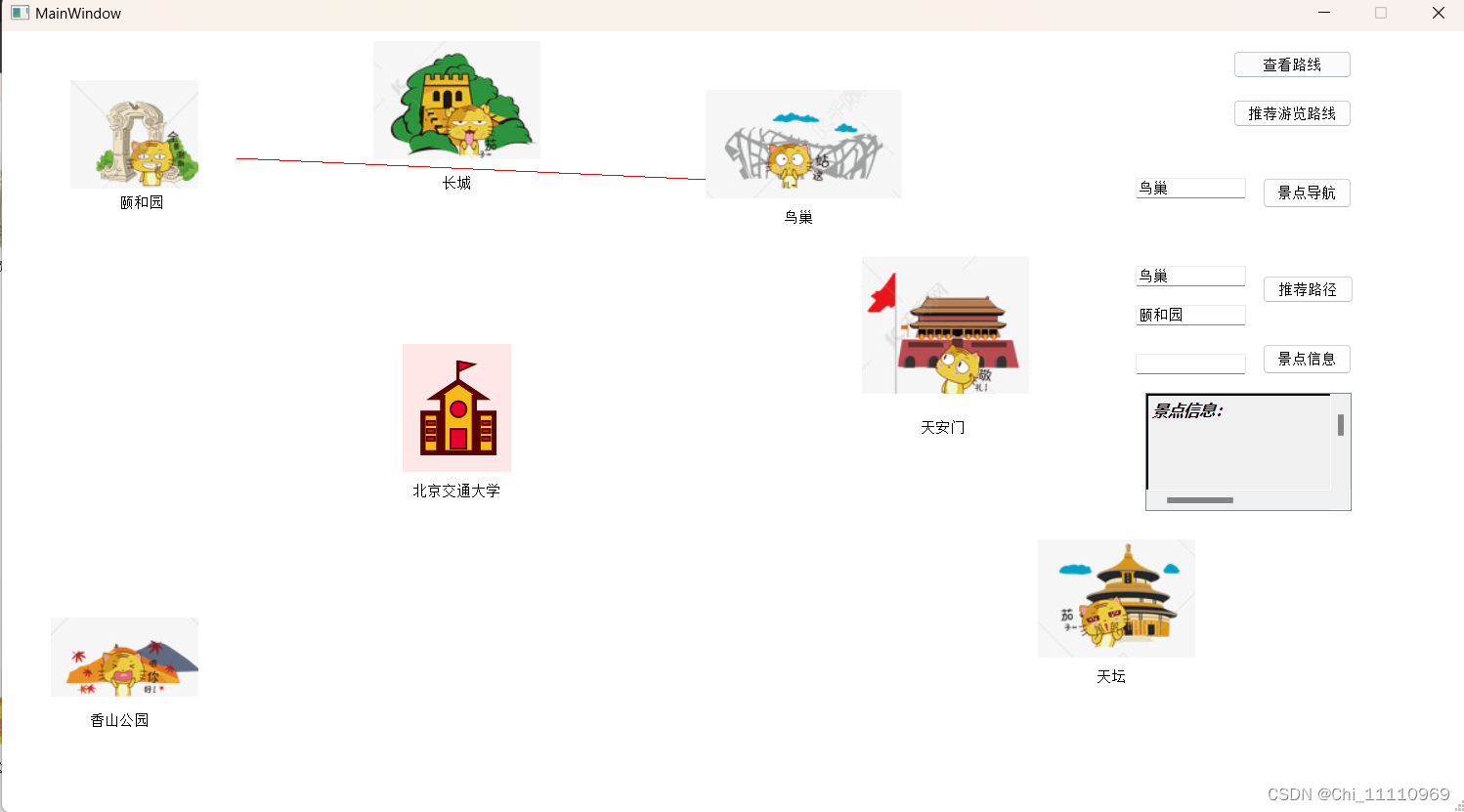
	输入一个景点名称，点击景点信息，在下方文字框中展示景点信息。

我在github上做的开源。