BMVC2021 | EMI-FGSM | 通过增强动量提升对抗样本的可迁移性

---

原文链接

本文 “Boosting Adversarial Transferability through Enhanced Momentum” 提出了增强动量迭代快速梯度符号法（EMI - FGSM），通过在迭代过程中额外积累前一次迭代梯度方向上采样数据点的梯度，显著提升了对抗样本的可迁移性。在标准 ImageNet 数据集上的实验表明，该方法能大幅提高基于动量攻击方法的对抗可迁移性，平均提升幅度达 11.1%。

---

摘要-Abstract

Deep learning models are known to be vulnerable to adversarial examples crafted by adding human-imperceptible perturbations on benign images. Many existing adversarial attack methods have achieved great white-box attack performance, but exhibit low transferability when attacking other models. Various momentum iterative gradient-based methods are shown to be effective to improve the adversarial transferability. In what follows, we propose an enhanced momentum iterative gradient-based method to further enhance the adversarial transferability. Specifically, instead of only accumulating the gradient during the iterative process, we additionally accumulate the average gradient of the data points sampled in the gradient direction of the previous iteration so as to stabilize the update direction and escape from poor local maxima. Extensive experiments on the standard ImageNet dataset demonstrate that our method could improve the adversarial transferability of momentum-based methods by a large margin of 11.1% on average. Moreover, by incorporating with various input transformation methods, the adversarial transferability could be further improved significantly. We also attack several extra advanced defense models under the ensemblemodel setting, and the enhancements are remarkable with at least 7.8% on average.

众所周知，深度学习模型容易受到对抗样本的攻击，这些对抗样本是通过在良性图像上添加人类难以察觉的扰动而生成的。许多现有的对抗攻击方法在白盒攻击中表现出色，但在攻击其他模型时，其对抗样本的可迁移性较低。各种基于动量迭代梯度的方法已被证明能有效提高对抗样本的可迁移性。在此，我们提出一种增强动量的迭代梯度方法，以进一步提升对抗样本的可迁移性。具体而言，在迭代过程中，我们不仅累积梯度，还额外累积在前一次迭代的梯度方向上采样得到的数据点的平均梯度，以此来稳定更新方向，避免陷入较差的局部极大值。 在标准ImageNet数据集上进行的大量实验表明，我们的方法平均可将基于动量的方法的对抗样本可迁移性大幅提高11.1%。此外，通过结合各种输入变换方法，对抗样本的可迁移性能够得到显著的进一步提升。我们还在集成模型设置下对多个先进的防御模型进行攻击，改进效果显著，平均提升幅度至少达到7.8%。

---

引言-Introduction

这部分主要介绍了研究背景和研究目的，指出深度学习模型易受对抗样本攻击，引出提高对抗样本可迁移性的研究方向，具体内容如下：

1. 深度学习模型的脆弱性及研究方向：深度学习模型在取得优异性能的同时，对对抗样本的脆弱性引发了安全敏感应用领域的严重担忧。这一问题促使研究分为两个方向，一是提高对抗样本的攻击性，二是增强神经网络对对抗样本的鲁棒性，二者相互促进。
2. 对抗攻击方法及可迁移性问题：近年来出现了众多对抗攻击方法，如基于一步梯度的攻击、迭代梯度攻击和基于优化的攻击等。现有攻击方法大多属于白盒攻击，虽在白盒设置下攻击性能良好，但对抗样本的可迁移性较低。而在黑盒攻击中，对抗样本的可迁移性是重要指标，它使在不了解模型内部机制的情况下攻击模型成为可能。
3. 提升可迁移性的现有方法及局限性：为提升白盒攻击对抗样本的可迁移性，已有方法包括将动量融入迭代梯度攻击、集成模型攻击、输入变换等。然而，在现有基于动量的攻击方法中，表现最佳的NI - FGSM在黑盒设置下平均攻击成功率仍低于52%，表明这些方法的改进效果有限。
4. 本文研究内容及成果预期：提出增强动量迭代快速梯度符号法（EMI - FGSM），通过在迭代过程中额外积累前一次迭代梯度方向上采样数据点的梯度，以稳定更新方向、找到更好的局部极大值，进而提升对抗样本的可迁移性。该方法在白盒和黑盒设置下都有望取得更高的攻击成功率。此外，EMI - FGSM能与集成模型攻击和各种输入变换方法互补，显著提升对抗样本在标准ImageNet数据集上的可迁移性。在攻击多个先进防御模型时，结合输入变换的EMI - FGSM平均攻击成功率可达86.6%，相比现有先进方法有明显提升 。

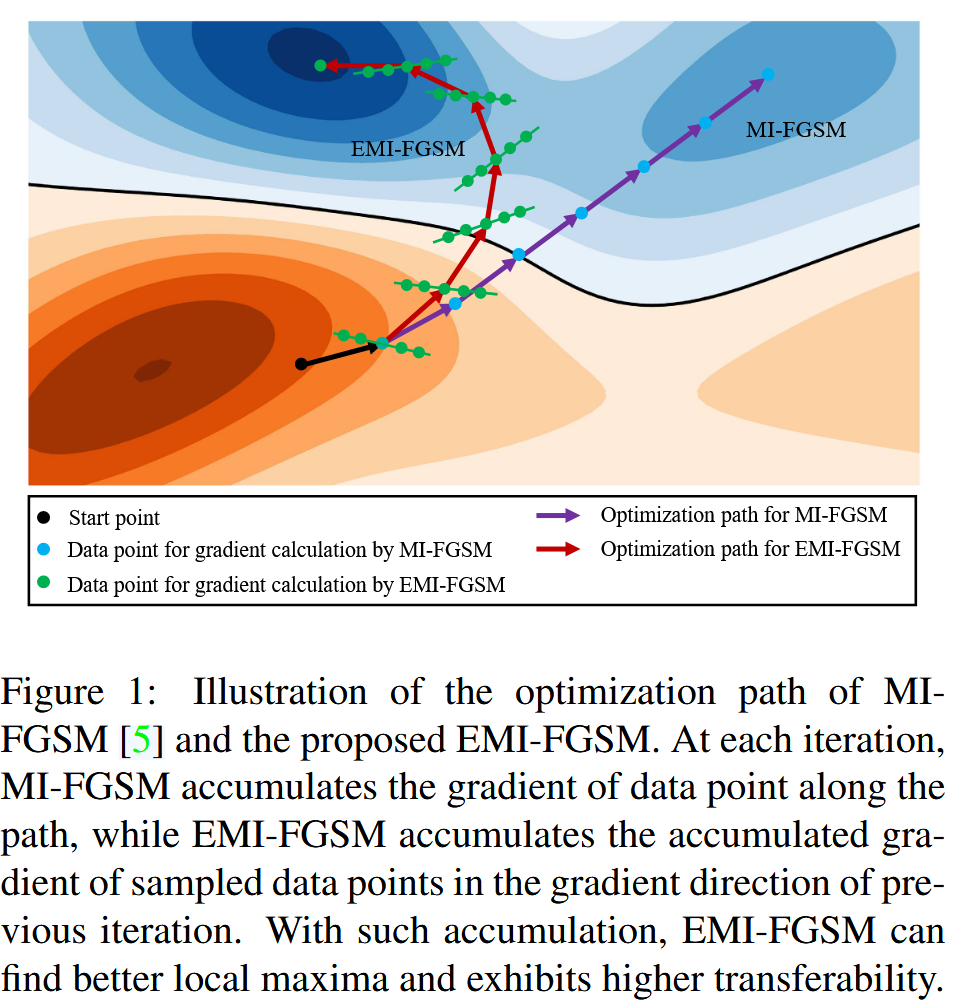
图1：MI-FGSM和本文提出的EMI-FGSM优化路径示意图。在每次迭代中，MI-FGSM沿着路径累积数据点的梯度，而EMI-FGSM则累积在前一次迭代梯度方向上采样数据点的累积梯度。通过这种累积方式，EMI-FGSM能够找到更好的局部极大值，展现出更高的可迁移性。

---

相关工作-Related Work

这部分主要介绍了与对抗攻击和防御相关的工作，为后续提出的方法和实验对比提供了基础，具体内容如下：

1. 对抗攻击
   • 攻击分类：根据攻击者对模型信息的获取程度，对抗攻击可分为白盒攻击和黑盒攻击。白盒攻击能访问模型的所有信息，而黑盒攻击仅能获取模型输出。同时，对抗样本在不同模型间具有可迁移性，基于此的攻击属于黑盒攻击。
   • 基于梯度的攻击方法：现有白盒对抗攻击多基于梯度优化扰动，虽攻击性能好，但可迁移性低。为提升可迁移性，出现了多种基于梯度的攻击方法。如MI - FGSM将动量融入迭代梯度攻击；NI - FGSM采用Nesterov加速梯度进一步增强可迁移性；集成模型攻击通过同时攻击多个模型来提高可迁移性。此外，输入变换也可增强对抗攻击的可迁移性，包括DIM（随机调整大小和填充输入）、TIM（在平移图像集合上优化扰动）、SIM（在多个尺度副本上优化对抗扰动），这些方法可与基于梯度的攻击方法结合使用。
2. 对抗防御：众多研究致力于增强深度学习模型的鲁棒性以防御对抗攻击。对抗训练是一种有前景的防御方法，其中集成对抗训练采用集成模型生成的对抗样本进行训练，对基于迁移的对抗攻击具有鲁棒性。此外，还有一些去噪或输入预处理方法，如HGD（用高级表示引导去噪器净化对抗样本）、R&P（对输入进行随机调整大小和填充），以及FD（基于JPEG的防御压缩框架）、Bit - Red（通过降低像素位深度检测对抗样本）和基于随机平滑（RS、ARS）的认证防御等方法。

---

方法-Methodology

基于梯度的对抗攻击-Gradient-based Adversarial Attacks

该部分主要介绍了几种典型的基于梯度的对抗攻击方法，为后续理解本文提出的新方法做了铺垫，具体内容如下：

1. 快速梯度符号法（FGSM）：FGSM是一种简单的基于梯度的对抗攻击方法，通过一步更新生成对抗样本。公式为$x^{adv}=x+ϵ\cdot sign({\nabla }_x{J}_f(x,y))$ ，其中$sign(\cdot )$是符号函数，${\nabla }_x{J}_f$表示损失函数关于$x$的梯度。这种方法直接利用当前样本的梯度信息来生成扰动，操作简单但过于直接，没有考虑迭代优化等更复杂的策略。
2. 迭代快速梯度符号法（I - FGSM）：I - FGSM是对FGSM的扩展，通过迭代应用梯度更新来生成对抗样本。其迭代公式为$x_{t+1}^{adv}=x_t^{adv}+\alpha \cdot sign({\nabla }_{x_t^{adv}}{J}_f(x_t^{adv},y))$，其中$x_1^{adv}=x$，$\alpha =ϵ/T$是一个小的步长，$T$是迭代次数 。相较于FGSM，I - FGSM通过多次迭代逐步优化扰动，能更有效地生成对抗样本，提高攻击成功率。
3. 动量迭代快速梯度符号法（MI - FGSM）：MI - FGSM为了实现更高的可迁移性，将动量概念融入迭代攻击中。计算过程分为两步，首先更新梯度$g_t=\mu \cdot g_{t-1}+\frac{{\nabla }_{x_t^{adv}}{J}_f(x_t^{adv},y)}{{\Vert {\nabla }_{x_t^{adv}}{J}_f(x_t^{adv},y)\Vert }_1}$，其中$g_{t-1}$是直到$(t-1)$次迭代累积的梯度，$\mu$是衰减因子且$g_0=0$；然后根据更新后的梯度更新对抗样本$x_{t+1}^{adv}=x_t^{adv}+\alpha \cdot sign(g_t)$。通过累积梯度，MI - FGSM能够稳定更新方向，逃离较差的局部极大值，从而提升对抗样本的可迁移性。
4. Nesterov迭代快速梯度符号法（NI - FGSM）：NI - FGSM将Nesterov加速梯度（NAG）集成到迭代攻击方法中，进一步改进对抗样本的可迁移性。计算时先得到中间变量${\overline{x}}_t^{adv}=x_t^{adv}+\alpha \cdot \mu \cdot g_{t-1}$，接着更新梯度$g_t=\mu \cdot g_{t-1}+\frac{{\nabla }_{{\tilde{x}}_t^{adv}}{J}_f({\tilde{x}}_t^{adv},y)}{{\Vert {\nabla }_{{\tilde{x}}_t^{adv}}{J}_f({\tilde{x}}_t^{adv},y)\Vert }_1}$，最后更新对抗样本$x_{t+1}^{adv}=x_t^{adv}+\alpha \cdot sign(g_t)$。NI - FGSM通过Nesterov加速梯度的“向前看”特性，使算法收敛更快，在寻找对抗样本时能更高效地探索参数空间，进而提高对抗样本的可迁移性。

预梯度引导动量攻击-Pre-gradient Guided Momentum based Attack

这部分内容提出了预梯度引导动量迭代快速梯度符号法（PI - FGSM），旨在探索更优的“向前看”方向以提升对抗攻击性能，具体内容如下：

1. 研究动机：NI - FGSM通过采用Nesterov加速梯度的“向前看”特性，在MI - FGSM基础上提升了对抗样本的可迁移性。但研究发现，NI - FGSM中积累动量所采用的方向并非“向前看”的最优方向。为探究更优方向，提出PI - FGSM。
2. 方法介绍：PI - FGSM在每次迭代时，通过前一次迭代的梯度来引导“向前看”。具体做法是，积累当前数据点加上前一次梯度后的数据点的梯度。其更新过程可概括为：首先计算 ${\tilde{x}}_t^{adv}=x_t^{adv}+\alpha \cdot {\tilde{g}}_{t-1}$，得到用于计算梯度的新数据点，其中 ${\tilde{g}}_{t-1}$ 是前一次迭代的梯度；接着计算该点的梯度 ${\tilde{g}}_t={\nabla }_{{\tilde{x}}_t^{adv}}{J}_f({\tilde{x}}_t^{adv},y)$；然后更新动量 $g_t=\mu \cdot g_{t-1}+\frac{{\tilde{g}}_t}{{\Vert {\tilde{g}}_t\Vert }_1}$ ，其中 $g_{t-1}$ 是之前累积的动量，$\mu$ 是衰减因子；最后根据更新后的动量更新对抗样本 $x_{t+1}^{adv}=x_t^{adv}+\alpha \cdot sign(g_t)$。
3. 方法优势：PI - FGSM不像NI - FGSM那样考虑所有历史梯度，而是利用局部梯度信息进行“向前看”引导。后续实验表明，这种方式能使PI - FGSM在攻击性能上表现更优，为提升对抗攻击的效果提供了一种新的思路和方法。

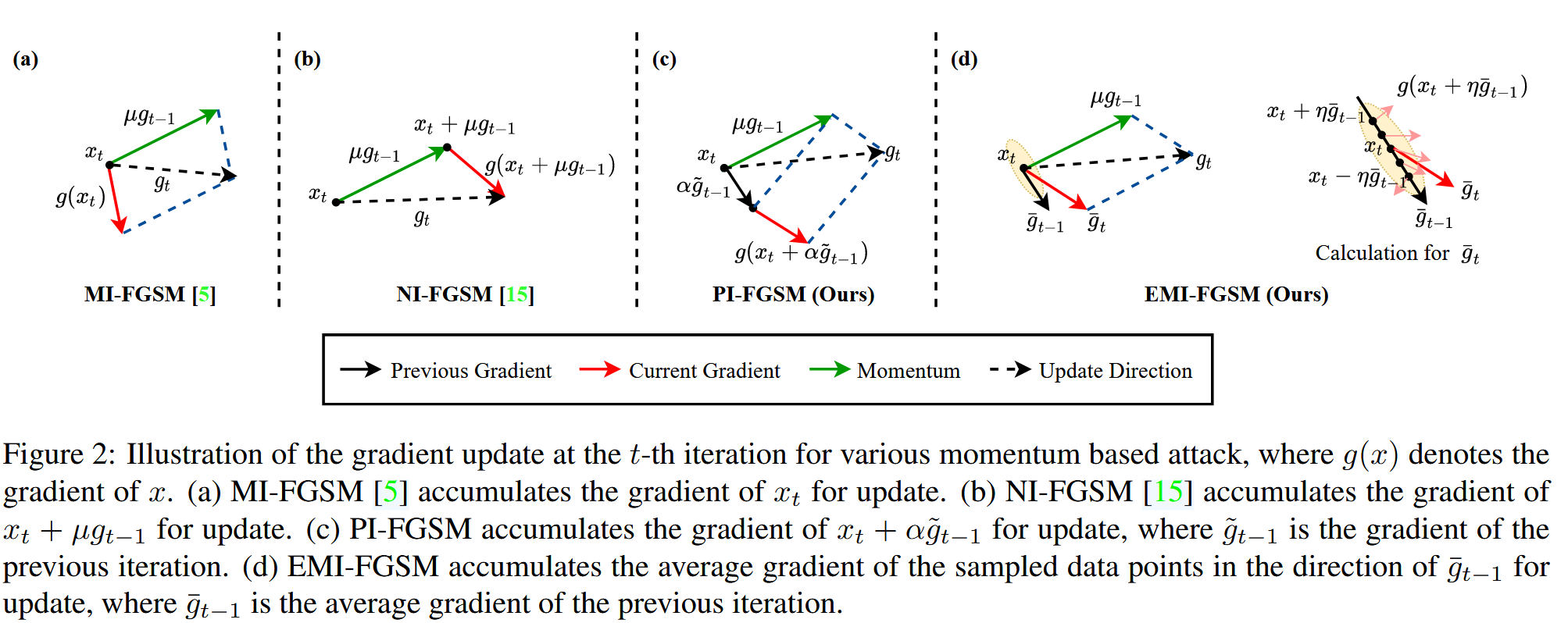
图2：各种基于动量的攻击在第t次迭代时的梯度更新示意图，其中 $g(x)$ 表示 $x$ 的梯度。
( a ) MI - FGSM通过累积 $x_t$ 的梯度进行更新。
( b ) NI - FGSM累积 $x_t+\mu g_{t-1}$ 的梯度进行更新。
( c ) PI - FGSM累积 $x_t+\alpha {\tilde{g}}_{t-1}$ 的梯度进行更新，其中 ${\tilde{g}}_{t-1}$ 是前一次迭代的梯度。
( d ) EMI - FGSM累积在 ${\bar{g}}_{t-1}$ 方向上采样数据点的平均梯度进行更新，其中 ${\bar{g}}_{t-1}$ 是前一次迭代的平均梯度。

增强动量攻击-Enhanced Momentum based Attack

该部分提出增强动量攻击（EMI - FGSM）方法，通过改进动量积累方式提升对抗样本可迁移性，具体内容如下：

1. 研究思路：基于对动量迭代梯度攻击方法的研究，发现积累梯度有助于生成高可迁移性对抗样本。受PI - FGSM启发，思考是否可通过积累当前数据点附近多个数据点的梯度，进一步提升攻击可迁移性。
2. 增强动量计算：在迭代过程中，不仅记忆过往梯度，还沿PI - FGSM的梯度方向（即前一次迭代的梯度方向）采样多个数据点，计算这些采样点的梯度。具体计算为，先计算第 $t$ 次迭代时采样的数据点 ${\overline{x}}_t^{adv}[i]=x_t^{adv}+c_i\cdot {\overline{g}}_{t-1}$ ，其中 $c_i$ 是在区间 $[-\eta ,\eta ]$ 采样的系数，${\overline{g}}_{t-1}$ 是前一次迭代计算的梯度；然后计算这些采样点的平均梯度 ${\overline{g}}_t=\frac{1}{N}{\sum }_{i=1}^N{\nabla }_{{\overline{x}}_t^{adv}[i]}{J}_f({\overline{x}}_t^{adv}[i],y)$，$N$ 为采样数量，该平均梯度即为增强动量。
3. EMI - FGSM算法：将增强动量融入I - FGSM得到EMI - FGSM，其更新过程为 $g_t=\mu \cdot g_{t-1}+\frac{{\overline{g}}_t}{{\Vert {\overline{g}}_t\Vert }_1}$，$x_{t+1}^{adv}=x_t^{adv}+\alpha \cdot sign(g_t)$ 。详细算法流程在Algorithm 1中给出，包括初始化参数、迭代采样计算梯度、更新动量和对抗样本，最终输出对抗样本。实验尝试不同采样方法后发现，沿PI - FGSM方向采样效果更好。

---

实验-Experiments

实验设置-Experimental Setup

该部分详细介绍了实验的设置情况，包括数据集、对比基线、实验模型、攻击设置等，为后续实验结果的可靠性和有效性提供了保障，具体内容如下：

1. 数据集：与以往研究类似，从ILSVRC 2012验证集中随机选取1000张图像作为实验数据。为保证实验的一致性和可比性，所有图像预先被调整大小为299×299×3 。
2. 对比基线：将本文提出的方法与四种基于梯度的攻击方法进行对比，包括FGSM、I - FGSM、MI - FGSM和NI - FGSM。同时，为进一步展示本文方法的性能优势，将其集成到集成模型攻击和基于输入变换的方法中，并与相应的基线进行对比。
3. 实验模型：实验选用了四类模型，包括四个正常训练的模型：Inception - v3（Inc - v3）、Inception - v4（Inc - v4）、Inception - Resnet - v2（IncRes - v2）、Resnet - v2 - 101（Res - 101）；三个集成对抗训练的模型：ens3 - advInception - v3（Inc - v3ens3 ）、ens4 - Inception - v3（Inc - v3ens4 ）、ens - adv - Inception - ResNet - v2（IncRes - v2ens ）；以及为验证方法有效性所采用的七个先进防御模型，涵盖NIPS 2017防御竞赛的前三名（如HGD、R&P等），还有随机平滑（RS）、对抗随机平滑（ARS）、特征蒸馏（FD）和位深度减少（Bit - Red）等防御方法对应的模型。
4. 攻击设置：遵循已有研究的设置，最大扰动 $ϵ=16/255$ ，像素值归一化到[0, 1]区间，迭代次数 $T=10$。对于动量项，设置衰减因子 $\mu =1$ 。针对不同的输入变换方法，分别设置相应参数：DIM的变换概率设为0.5，输入图像先随机调整大小为 $r\times r\times 3$（$r\in [299,330)$），再填充为330×330×3；TIM采用7×7的高斯核；SIM的尺度副本数量设为 $m=5$；对于EMI - FGSM，设置采样数量 $N=11$ ，采样区间边界 $\eta =7$ ，并采用线性采样方式。

基于梯度攻击的比较-Comparison with Gradient-based Attacks

这部分主要对比了不同基于梯度的攻击方法在单模型和集成模型设置下的攻击成功率，以评估本文提出的PI-FGSM和EMI-FGSM的性能，具体内容如下：

1. 单模型设置：在单模型设置下，以在Inc-v3上生成的对抗样本为例进行攻击实验。结果显示，除FGSM外，其他攻击方法在白盒设置下都能达到100%的攻击成功率。在黑盒攻击中，I-FGSM的可迁移性甚至低于FGSM。与MI-FGSM和NI-FGSM相比，PI-FGSM在正常训练模型上的可迁移性高8 - 9%，在对抗训练模型上高0.8 - 1.5%。而带有增强动量的EMI-FGSM在正常训练模型和对抗训练模型上都展现出更高的可迁移性，分别比PI-FGSM高10.5 - 12.5%和4.4 - 5.4%，平均比强大的基线NI-FGSM高出11.1% 。
   
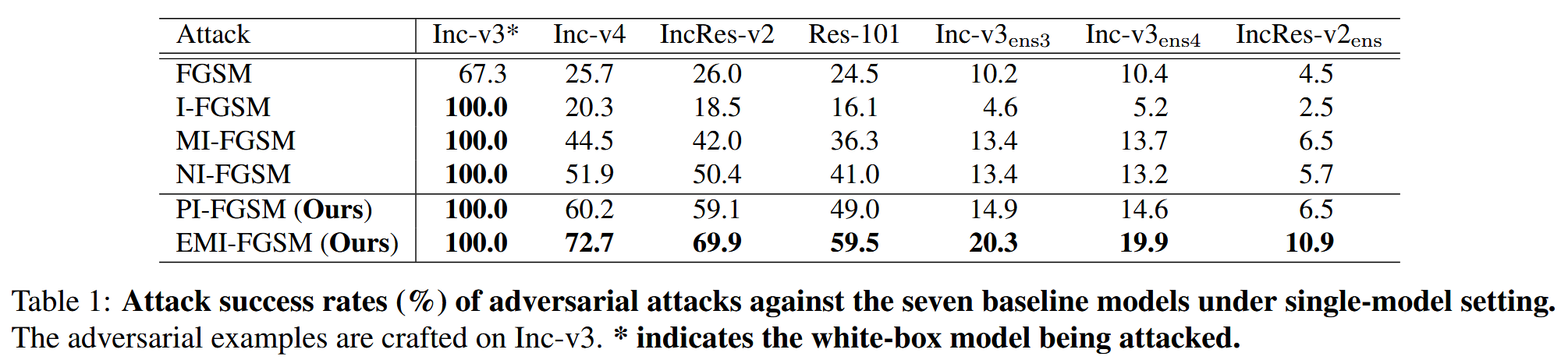
   表1：单模型设置下对抗攻击对七个基线模型的攻击成功率（%）。对抗样本在Inception-v3（Inc-v3）模型上生成。$\ast$表示被攻击的白盒模型。

2. 集成模型设置：在集成模型设置下，将四个正常训练模型（Inc-v3、Inc-v4、IncRes-v2和Res-101）的logit输出以相等的权重融合来实施攻击。结果表明，PI-FGSM在白盒设置下的攻击成功率高于I-FGSM和MI-FGSM，在三个对抗训练模型上的可迁移性也显著提高，验证了由于NI-FGSM考虑过多历史梯度，其积累的动量方向不如PI-FGSM精确，并非最优的“向前看”方向。此外，EMI-FGSM在白盒和黑盒设置下都取得了最佳结果，比强大的基线NI-FGSM高出20%以上，充分证明了所提出的增强动量的高效性。
   
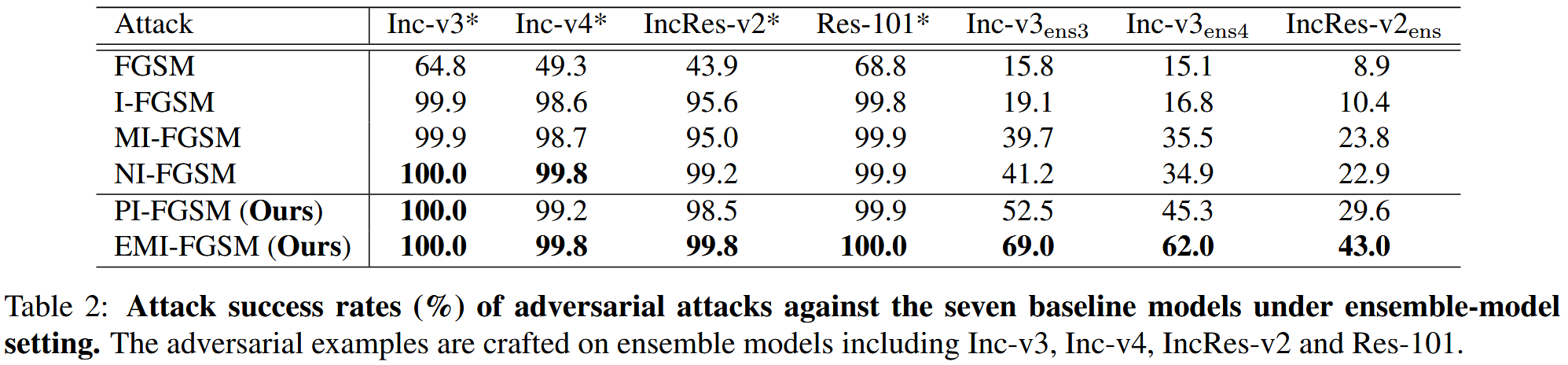
   表2：集成模型设置下对抗攻击对七个基线模型的攻击成功率（%）。对抗样本是在包含Inception-v3（Inc-v3）、Inception-v4（Inc-v4）、Inception-Resnet-v2（IncRes-v2）和Resnet-v2-101（Res-101）的集成模型上生成的。

与基于变换的攻击集成-Integrated With Transformation-based Attacks

这部分主要研究了将EMI-FGSM与多种基于输入变换的攻击方法相结合后的效果，在单模型和集成模型两种设置下进行实验，结果表明结合后的方法显著提升了攻击成功率和对抗样本的可迁移性。具体内容如下：

1. 研究方法：分别在单模型和集成模型设置下，将EMI-FGSM与多种输入变换方法（DIM、TIM、SIM以及三者结合的DTS）相结合。为保证实验公平性，将所有这些变换方法也集成到MI-FGSM作为基线进行对比。

2. 单模型设置结果：以在Inc-v3上生成的对抗样本攻击其他模型的实验结果为例，发现EMI能够显著提升每种基于变换的攻击方法的可迁移性。总体而言，基于EMI的攻击方法始终优于基线攻击方法，攻击成功率提升范围在3.9% - 32.4%。即便在白盒设置下，EMI也能进一步提高基线攻击的成功率，如EMI-DTS对比DTS，对Inc-v3的攻击成功率提升了0.7%。在其他三个正常训练模型上生成对抗样本进行攻击的实验结果与在Inc-v3上的结果一致。
   
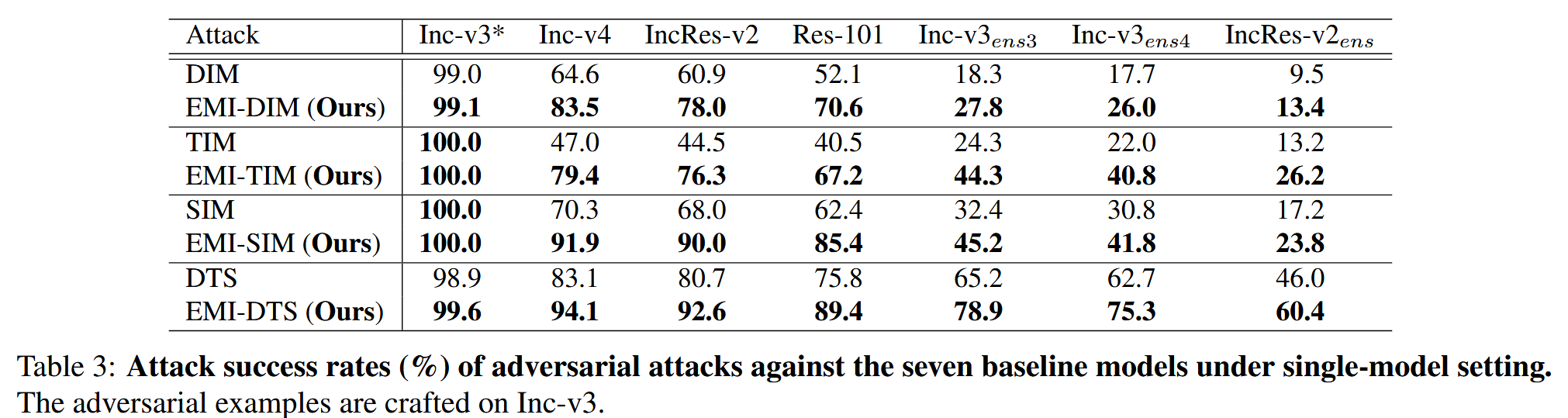
   表3：单模型设置下针对七个基线模型的对抗攻击成功率（%）。对抗样本在Inception - v3（Inc - v3）模型上生成。

3. 集成模型设置结果：同样在集成模型设置下进行评估，结果显示基于EMI的方法在所有实验中都显著提高了攻击成功率。特别是最终结合的EMI-DTS在对三个对抗训练模型的黑盒攻击中，攻击成功率超过94.1%。这些结果有力地证明了将EMI-FGSM、输入变换和集成模型攻击相结合，能够有效提高攻击的可迁移性。
   
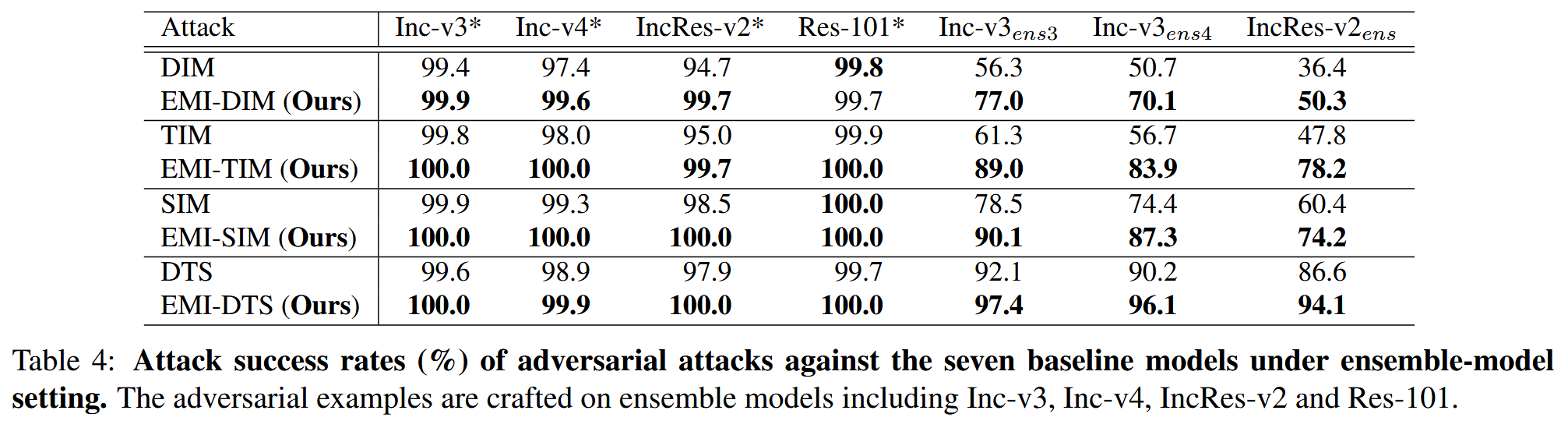
   表4：集成模型设置下针对七个基线模型的对抗攻击成功率（%）。对抗样本在由Inception - v3、Inception - v4、Inception - ResNet - v2和ResNet - v2 - 101组成的集成模型上生成。

攻击先进的防御模型-Attacking Advanced Defense Models

这部分主要评估了EMI-FGSM在集成模型设置下，结合多种输入变换对七个先进防御模型的攻击效果，结果显示EMI-FGSM显著提升了攻击的可迁移性，凸显了现有防御方法的不足。具体内容如下：

1. 实验目的：在前面实验已证明EMI-FGSM能显著提升攻击基线的基础上，进一步评估其在集成模型设置下，结合多种输入变换对先进防御模型的攻击效果，以展示该方法的高效性。
2. 实验设置：所有对抗样本均在集成模型（包括Inc-v3、Inc-v4、IncRes-v2和Res-101）上生成，然后用这些对抗样本测试七个先进防御模型。
3. 实验结果：EMI-FGSM显著提升了三种基于变换的攻击（DIM、TIM、SIM）在所有防御模型上的可迁移性，平均性能分别提升了14.8%、24.5%和11.8%。将三种输入变换结合（DTS）并集成到EMI-FGSM中，进一步提升了可迁移性。EMI-DTS的平均攻击成功率达到86.6%，比现有最先进的方法大幅提高了7.8%。
4. 结果分析：考虑到对抗样本是在没有任何防御机制的集成模型上生成，却能取得如此高的攻击性能，这表明现有防御方法效率较低，距离在实际应用中的部署还有很大差距。

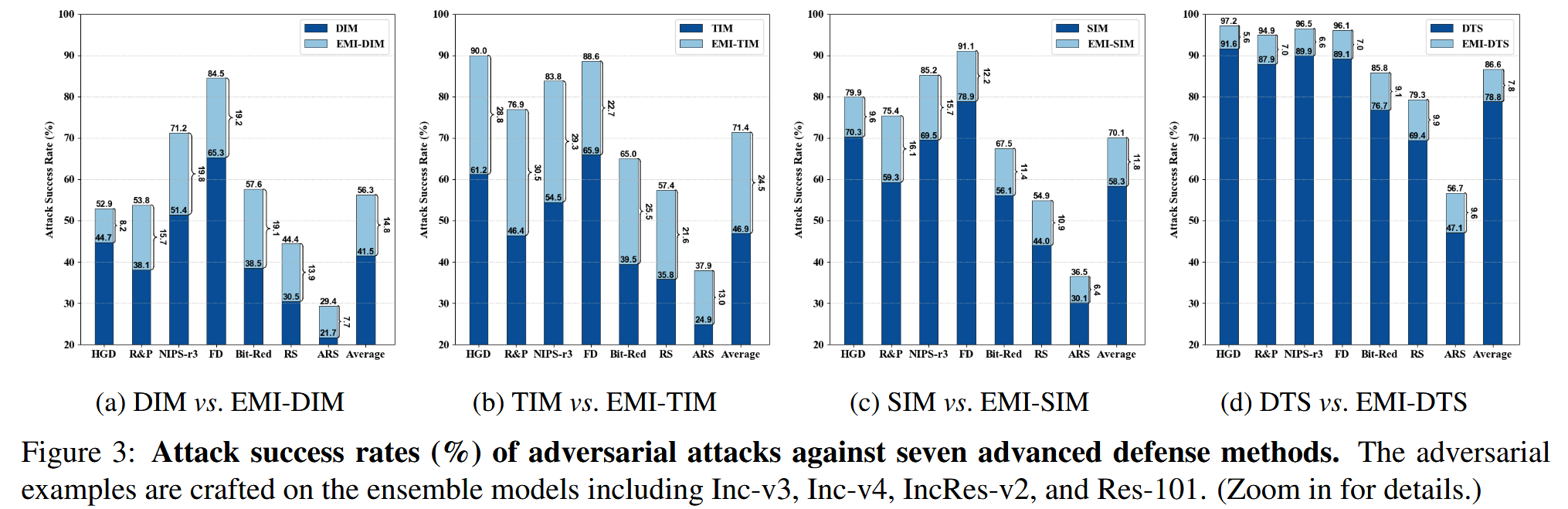
图3：针对七种先进防御方法的对抗攻击成功率（%）。对抗样本在由Inception - v3、Inception - v4、Inception - ResNet - v2和ResNet - v2 - 101组成的集成模型上生成。（如需查看细节请放大。）

消融研究-Ablation Study

这部分通过消融实验，研究了采样方法、采样间隔和采样数量对基于增强动量方法性能的影响，为确定最佳实验参数提供依据，具体内容如下：

1. 研究目的：深入探究基于增强动量的方法（如EMI - FGSM和EMI - DTS）性能提升的原因，分析采样方法、采样间隔 $\eta$ 和采样数量 $N$ 这些因素对其性能的影响。

2. 实验设置：为简化分析，仅考虑在Inc - v3模型上由普通EMI - FGSM和EMI - DTS生成的对抗样本的可迁移性。默认设置采用线性采样，$\eta =7$，$N=11$ 。

3. 采样方法的影响：测试了线性采样、均匀采样和高斯采样三种方法对EMI - FGSM和EMI - DTS性能的影响。结果表明，三种采样方法都比攻击基线具有更高的可迁移性，且性能相近。其中线性采样的结果略高，所以在实验中采用线性采样。
   
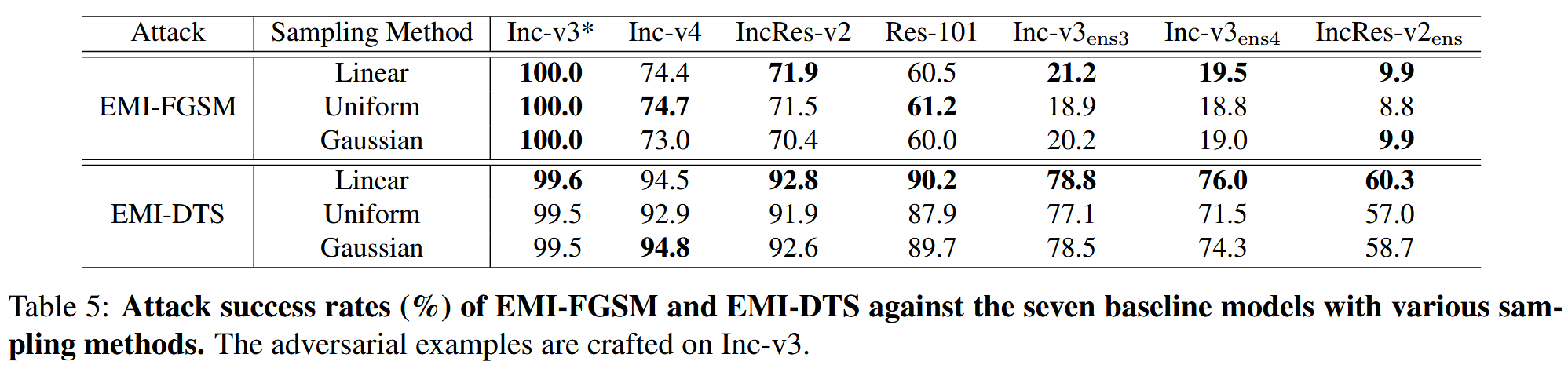
   表5：采用不同采样方法时，EMI - FGSM和EMI - DTS对七个基线模型的攻击成功率（%）。对抗样本在Inception - v3（Inc - v3）模型上生成。

4. 采样间隔的影响：尝试了 $\eta$ 从1到10的不同值，发现对于所有 $\eta$ 值，白盒攻击成功率均为100%。对于EMI - FGSM和EMI - DTS，当 $\eta \le 3$ 时，可迁移性增加；在 $4\le \eta \le 7$ 范围内，攻击的可迁移性相似；当 $\eta >7$ 时，性能略有下降。因此，实验选择 $\eta =7$。
   
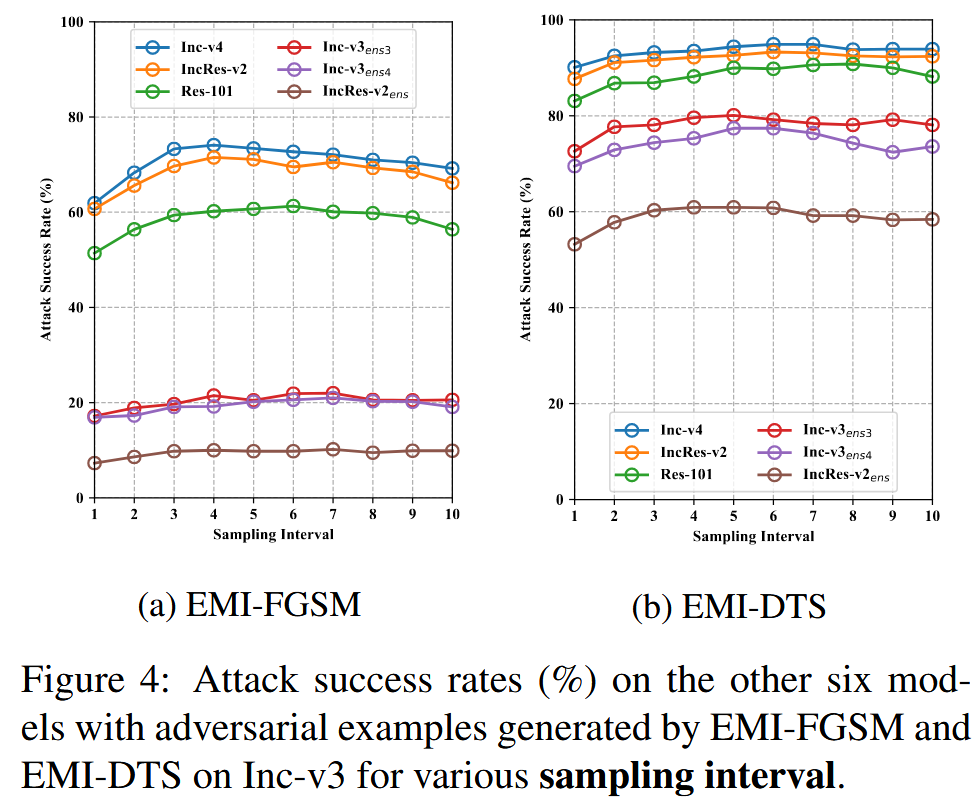
   图4：在Inception - v3（Inc - v3）上由EMI - FGSM和EMI - DTS生成的对抗样本，针对其他六个模型，在不同采样间隔下的攻击成功率（%）。

5. 采样数量的影响：研究发现，对于不同的(N)值，白盒攻击成功率均为100%。当 $N=1$ 时，EMI - FGSM退化为MI - FGSM，可迁移性最低。随着 $N$ 增加，EMI - FGSM在 $N=11$ 前、EMI - DTS在 $N=7$ 前可迁移性迅速提升。$N>11$ 时，增加 $N$ 仍能为EMI - FGSM带来少量性能提升，但会增加计算成本。综合考虑性能提升和成本，实验设置 $N=11$ 。
   
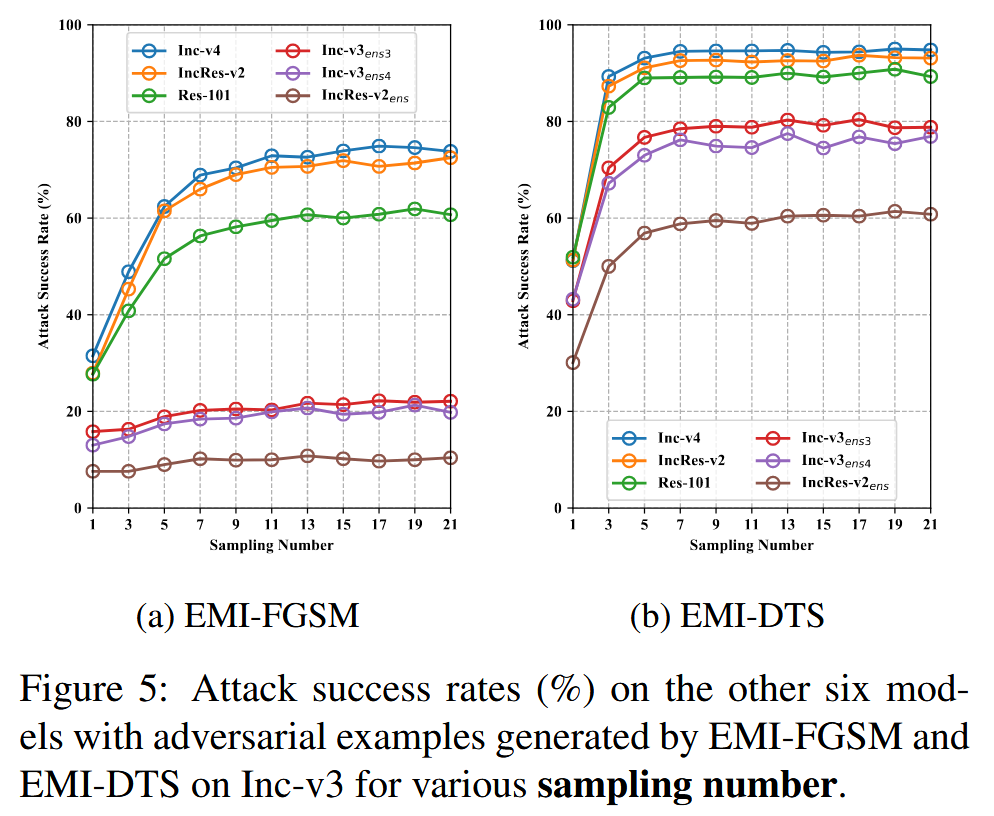
   图5：在Inception - v3（Inc - v3）上由EMI - FGSM和EMI - DTS生成的对抗样本，针对其他六个模型，在不同采样数量下的攻击成功率（%）。

关于可能变体的讨论-Discussion on Possible Variations

这部分探讨了除EMI - FGSM外其他增强动量的可能实现方式，对比分析了它们与EMI - FGSM的性能差异，具体内容如下：

1. 提出其他增强动量的变体：提出ENI - FGSM和ERI - FGSM两种增强动量的可能实现方式。ENI - FGSM在采样数据点时，方向基于前一次迭代的累积动量，即 ${\overline{x}}_t^{adv}[i]=x_t^{adv}+c_i\cdot g_{t-1}$ ；ERI - FGSM则是对随机采样的数据点累积梯度，其采样公式为 ${\overline{x}}_t^{adv}[i]=x_t^{adv}+\alpha \cdot U\left(-1^d,1^d\right)$，其中 $U(a,b)$ 表示在 $[a,b]$ 上的均匀分布。
2. EMI - FGSM与ENI - FGSM对比：从NI - FGSM的角度出发，思考能否在第 $t$ 次迭代时，累积动量方向上数据点的梯度。为此扩展NI - FGSM得到ENI - FGSM并测试其攻击性能。实验结果表明，ENI - FGSM的攻击性能明显低于EMI - FGSM，这进一步支持了“累积动量方向不能精确描述邻域，难以找到合适的梯度计算点”的假设，因为累积动量包含了过多前序迭代的信息。
3. EMI - FGSM与ERI - FGSM对比：由于ENI - FGSM和EMI - FGSM均在固定方向采样数据点，考虑在第 $t$ 次迭代时，累积 $x_t^{adv}$ 邻域内数据点的梯度会产生怎样的效果，进而测试ERI - FGSM在不同模型上的性能。结果显示，ERI - FGSM在正常训练模型上的可迁移性远低于EMI - FGSM，但在对抗训练模型上性能稍好。推测原因是用于梯度计算的带噪声数据点与对抗训练中的对抗样本更相似。

图6：单模型设置下，EMI - FGSM、ERI - FGSM和ENI - FGSM对七个模型的攻击成功率（%）。

---

结论-Conclusion

本文提出了一种增强动量的方法，将其融入迭代梯度攻击中有效提升了对抗攻击能力，同时揭示了现有防御方法的不足，具体结论如下：

1. 方法有效性：受现有基于动量的攻击方法启发，提出的增强动量方法不仅积累每次迭代的梯度，还积累前一次迭代梯度方向上采样数据点的梯度。将该方法融入迭代梯度攻击后，在标准ImageNet数据集上的实验表明，无论是白盒还是黑盒设置下，攻击成功率都显著提高。
2. 组合方法优势：集成现有输入变换的EMI - DTS，在集成模型设置下展现出极高的对抗样本可迁移性，平均黑盒攻击成功率超过94%。这表明将增强动量方法与输入变换、集成模型攻击相结合，能极大地提升攻击效果。
3. 现有防御的不足：使用提出的方法攻击先进防御模型的实验结果显示，现有防御方法的效果不佳，距离实际应用还有很大差距。这意味着需要进一步研究并开发更强大的鲁棒深度学习模型，以应对对抗攻击的威胁。