【优化求解】基于自然选择和随机扰动改进磷虾群算法matlab源码-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_59747472/article/details/120147284

1、磷虾群算法(KH)

由来：根据磷虾群觅食的特性，由Gandomi等在2012年首次提出[1]。在运动过程中，磷虾群不断地聚集以增大种群密度，并减少被捕食的几率，同时探索生存区域，尽可能缩短它们与食物的距离，最终使得种群获得食物。

算法描述：

1、磷虾个体的速度（位置X的微分）更新公式：

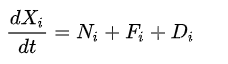
解释：磷虾群位置的变化受到三种影响：邻居磷虾的诱导，食物位置的影响和扰动

诱导运动N

诱导运动指的是，每一个磷虾个体会受到其一定范围内的邻居磷虾个体和最佳位置的个体的影响。其形式化表达为：

觅食运动F

类似于诱导运动，觅食运动包含两个部分，第一部分是食物位置，第二部分是先前关于食物位置的经验。表达形式是：

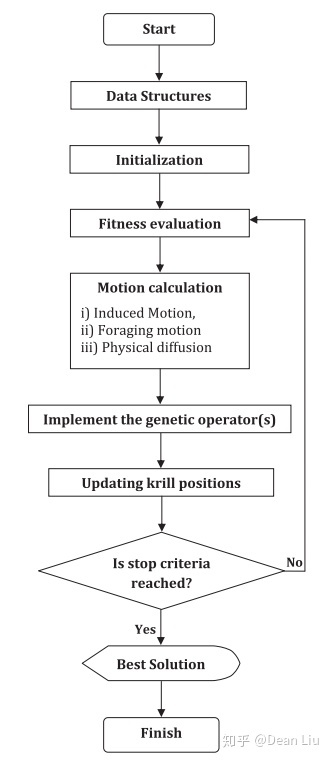
4、最后给出算法步骤和流程图

I. Data Structures: 定义边界，确定算法参数（种群规模Np，最大迭代次数t^max，最大诱导速度N^max，最大觅食速度V_f，最大随机扩散速度D^max，诱导惯性权重w_n，觅食惯性权重w_f和步长缩放因子C_t）等.
II. Initialization: 在搜索空间里随机产生初始种群.
III. Fitness evaluation: 根据磷虾的位置对每个磷虾个体进行评估（适应值函数计算/优化目标函数计算）.
IV. Motion calculation:速度分量计算，计算运动速度和位置
* Motion induced by the presence of other individuals
* Foraging motion
* Physical diffusion
V. Implement the genetic operators：多只采用交叉操作
VI. Updating: 在搜索空间内更新个体位置.
VII. Repeating:t=t+1，返回步骤 III 直到满足停止条件（最大迭代次数t^max）.
VIII. End

2、改进的磷虾群算法(ANRKH)

（1）觅食权重和运动权重的时变非线性递减策略

二、仿真实验与分析

为了验证ANRKH算法的性能，本文将ANRKH算法与两种相关算法—KH 算法和KHLD算法进行比较。以文献[1]中的f2、f3、f5为例。为了保证测试算法的公平性，3种算法中共同的参数设置如下：磷虾个体数目N P = 100 NP=100NP=100，最大迭代次数t m a x = 1000 t_{max}=1000tmax=1000，最大诱导速度N m a x = 0.001 N^{max}=0.001Nmax=0.001，最大觅食速度V f = 0.02 V_f=0.02Vf=0.02，最大随机扩散速度D m a x = 0.005 D^{max}=0.005Dmax=0.005；3种算法中不同的参数取值见表1；每个函数进行30次独立数值实验。

表1 KH、KHLD和ANRKH中的参数取值

在这里插入图片描述结果显示如下：

函数：F2
KH：最大值: 124.3161,最小值:28.6977,平均值:43.0134,标准差:29.4007
KHLD：最大值: 101.6416,最小值:26.2886,平均值:30.2278,标准差:13.5046
ANRKH：最大值: 81.6635,最小值:24.9959,平均值:28.6219,标准差:12.2347
函数：F3
KH：最大值: 0.91102,最小值:0.37651,平均值:0.60851,标准差:0.12396
KHLD：最大值: 0.024535,最小值:0.0063132,平均值:0.013014,标准差:0.0046107
ANRKH：最大值: 9.4045e-07,最小值:1.4627e-07,平均值:5.5261e-07,标准差:1.9059e-07
函数：F5
KH：最大值: 0.27584,最小值:0.18773,平均值:0.22487,标准差:0.024735
KHLD：最大值: 0.038433,最小值:0.019181,平均值:0.027884,标准差:0.0054838
ANRKH：最大值: 0.00044475,最小值:0.00026492,平均值:0.00033714,标准差:4.5962e-05

由此可以看出，ANRKH算法能够有效地避免陷入局部最优，在全局搜索和局部勘探能力上有着显著优势。

三、参考文献

[1] 刘沛, 高岳林, 郭伟. 基于自然选择和随机扰动的改进磷虾群算法[J]. 小型微型计算机系统, 2017, 38(8): 1845-1849.
[2] Li J , Tang Y , Hua C , et al. An improved krill herd algorithm: Krill herd with linear decreasing step[J]. Applied Mathematics & Computation, 2014, 234:356-367.
[3] Gandomi A H, Alavi A H. Krill Herd:a new bio- inspired optimization algorithm[J]. Commun Nonlinear Sci Numer Simul, 2012, 17(12) : 4831-4845.