【算法】浅析二分-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_59256973/article/details/134152068

本文介绍了二分算法的核心思想，包括确定边界、两种模板（从左/右逼近）的应用，以及一个整数二分的具体C++实例。作者强调了理解边界条件的重要性，并分享了学习心得。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

写计组的作业真的有点痛苦，摸一个博客，记录一下之前学习二分算法的一点的理解，可能讲的不好，有兴趣可移步y总acwing看看原视频。

二分的本质

一堆元素中（有序无序都行），有一部分满足某个性质，另一部分不满足这个性质，二分的本质，其实可以看作是对这个边界的确定，也就是把一堆元素按照一个条件精准划分成2部分。

所有的程序中二分出来的必然是会有结果的，然而具体问题具体分析，可能实际上还有一些其他条件。

2个模板的思路

先放图（？）

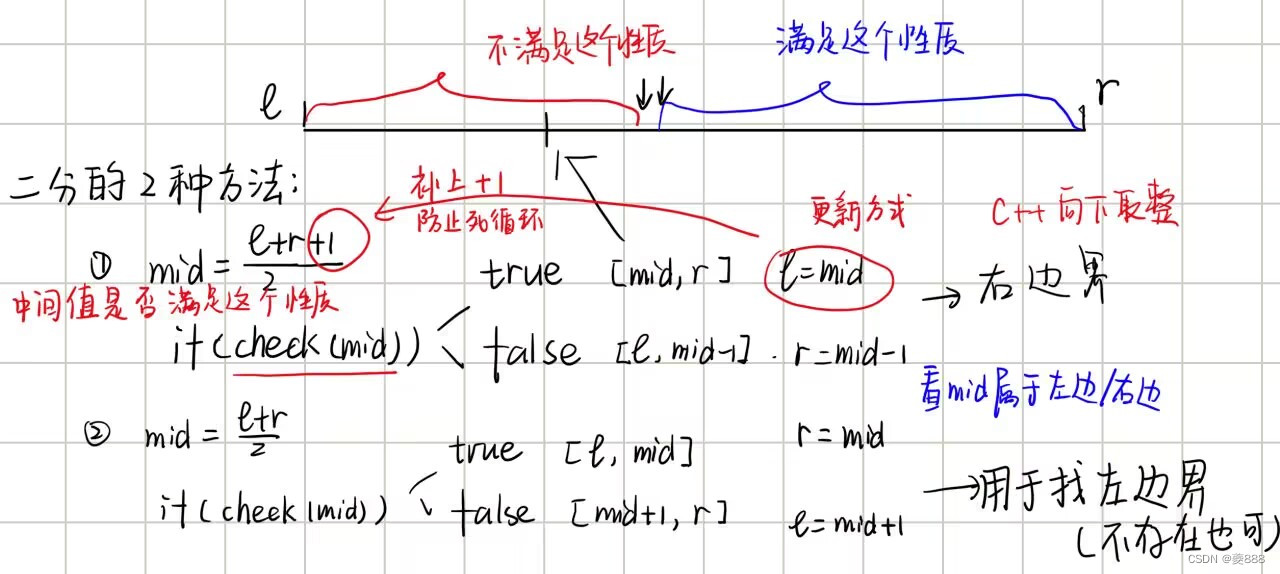
第1个板子是从左边开始逼近的，用于寻找右边界，具体步骤描述如下：

说到二分，肯定会用到中间值啦！先令中间值 $mid=\frac{l+r+1}{2}$ ， $l$ 是左边界元素的下标， $r$ 是右边界元素下标。
然后我们需要写一个 $check()$ 函数，来检验 $mid$ 位置的元素是否满足左边区域的性质。
若满足当前区域性质->true，我们下一次寻找左右边界位置的范围区间变为： $[mid,r]$ ，下一轮的数据条件更新为： $l=mid$ 。
若不满足当前区域性质->false，我们下一次寻找左右边界位置的范围区间变为： $[l,mid-1]$ ，下一轮的数据条件更新为： $r=mid-1$ 。
进入步骤1，一直到二分出结果为止。

ps:这里有一点需要注意， $mid=(l+r+1)/2$ 。为什么要加1呢？原因是，当我们按照步骤3中的方式 $l=mid$ 来更新数据时，如果是 $mid=(l+r)/2$ ：

假设初值： $l_{0}=0,r_{0}=2,mid_{0}=1$
第1轮更新后： $l_{1}=mid_{0}=1,r_{1}=2,mid_{1}=1$
第2轮更新后： $l_{2}=mid_{1}=1,r_{2}=2,mid_{2}=1$
......

咦？我们惊奇的发现，由于向下取整，这个时候居然陷入死循环了，所以从左边逼近的时候需要补上+1哦。

另一种板子，从右边开始逼近，推的过程与此同理。

举个例子：整数二分

整数二分的例子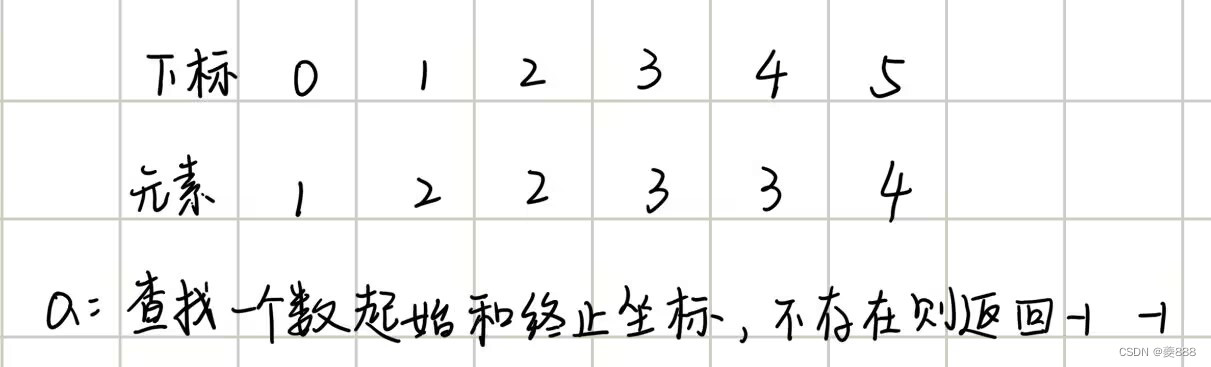

大家想想，是不是从右边的部分开始划分，尝试寻找左边界，得到的就是对应元素的起始坐标，同理，从左边的部分开始划分，尝试寻找右边界左边开始逼近，寻找右边界，得到的就是对应元素的终止坐标。

C++代码实现看这里，可以尝试自己先写一写，再运行调试看看逻辑。

#include <iostream>
using namespace std;
const int N=1e6+10;
int n,q[N],k;
int main()
{
    scanf("%d%d",&n,&k);
    for(int i=0;i<n;i++)scanf("%d",&q[i]);
    while(k--)
    {
        int x;
        scanf("%d",&x);
        int l=0,r=n-1;
        //出循环的时候，l=r
        while(l<r)
        {
            //第一种，mid不需要加1，从右边的部分开始划分，在尝试寻找左边界
            int mid=l+r>>1;
            if(q[mid]>=x)r=mid;
            else l=mid+1;
        }
        //没有找到
        if(q[l]!=x)printf("-1 -1\n");
        //下面寻找右边界
        else
        {
            //先打印左边界
            printf("%d ",l);
            int l=0,r=n-1;
            while(l<r)
            {
                //第二种，mid加1，从左边的部分开始划分，在尝试寻找右边界
                int mid=l+r+1>>1;
                if(q[mid]<=x)l=mid;
                else r=mid-1;
            }
            cout<<l<<endl;
        }
    }
    return 0;
}