跟着鲁sir学CV_Opencv（4）尺度不变 SIFT

解决尺度不变，拉普拉斯

问题：解决尺度不变（scale covariance）问题（角点存在这个问题）

角点见（3）

解决：找对应函数

纵轴：圆圈准确度，横轴圆半径，顶点看出最准确时候的半径

拉普拉斯找二阶导，但是随着σ增大，信号衰减没了

可以补充，防止衰减影响

二阶拉普拉斯模板

现在推导圆半径与窗宽有何关系

只有左边这个正好的合适

拉普拉斯，一阶高斯偏导卷积最大，高斯二阶偏导=0，需要：

则

关系求出！

也就是找到这个0平面，为我要的圈（框住了特征）

然后检查图的响应结果，对每个点判断，算出对应r，然后3个里面比较做决策，在26个点里进行非最大化抑制

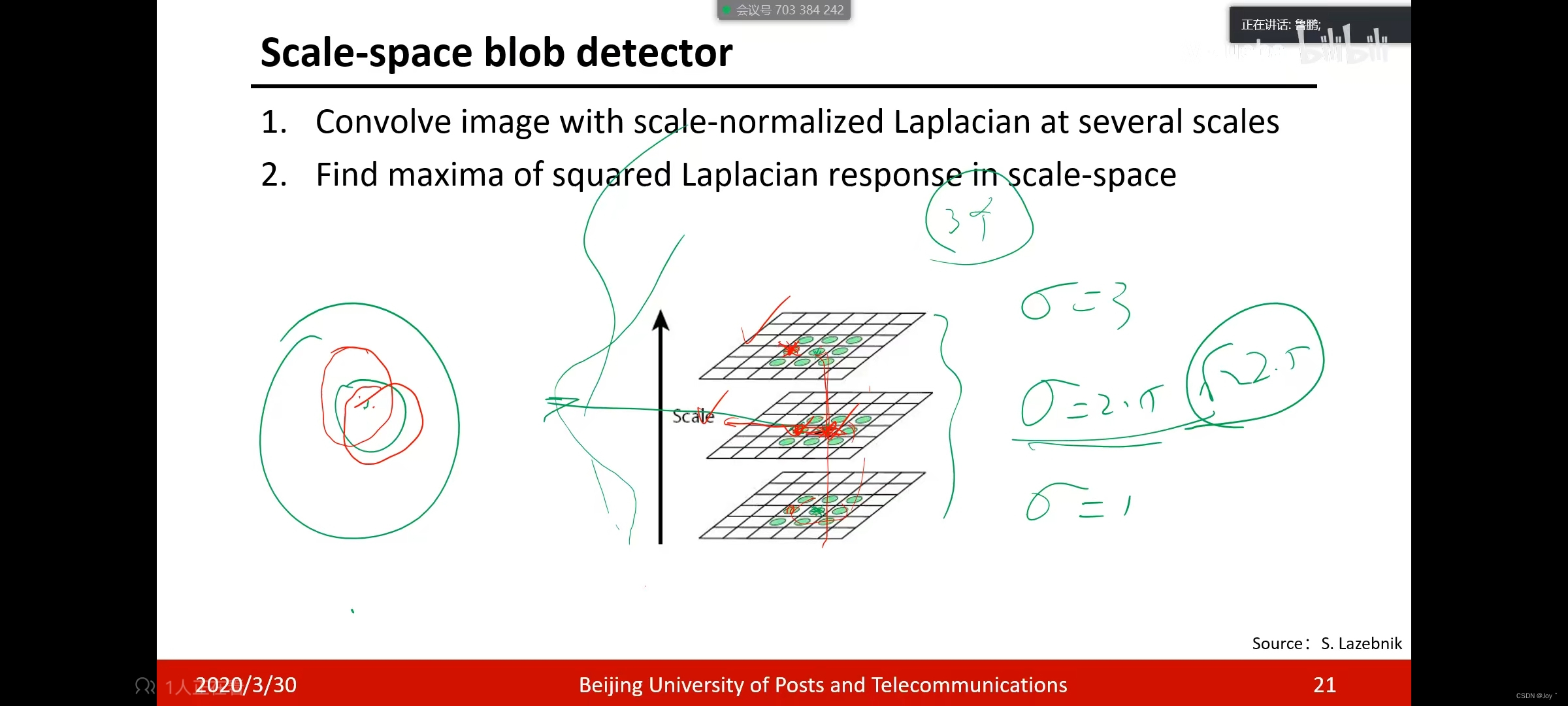
缺陷

对每个点判断，而且还要高斯模板，检验各种尺度，运算太慢

优势

精确找圆

改进1 将角点与尺度结合

只判断角点周围的，减少更多运算

改进2 SIFT 尺度不变特征

特征提取圈住

DoG效果近似拉普拉斯

 用小西格玛减去大，大的更模糊，提取关键信息

差异是k-1

 可以在基础上一层层做，效率更高

优势

用上一次的结果得到大核

把图缩小，窗口不变，检测

检查n倍尺度，把图缩小n倍，同样模板卷积就行了

基于2的改进3 分组做DoG和缩放

我们可以先用下面的在原图上做尺度1-2的，然后在上面做缩放，做尺度2-4的，可以与1-2的结果拼接。同理，可以继续做4上的缩放，做4-8的。每个阶段反复看都是1-2。

也就是将1-8分阶段处理，使用两个改进，一个是原图DoG，另一个是原图等比缩放但是高斯模板尺度不变。

 实际做的时候，64隔点采样，用32

关于s，怎么选择让尺度变化连续

在原图DoG过程中，左边五个才能推出右边四个，右边四个经过非最大化抑制，推出2个，与上面的原图缩放要连续

 但是SIFT对视角变化有影响

可以针对梯度变化进行拉伸，使得圆变成椭圆正好圈住特征

 压扁过程

比较特征点

但是可能存在进行比较的时候，如果两张图拍摄都是平面角度相同还好，相当于等比例放大，但是有的会发现两个特征存在角度差异的问题

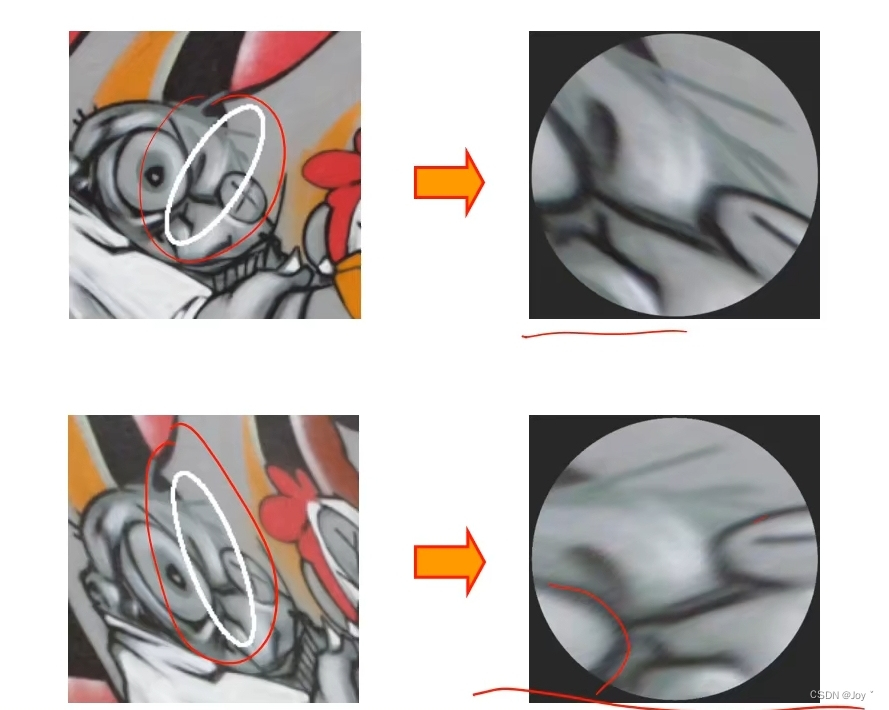
 我们就计算圆（椭圆）内的所有点的梯度幅度（强度）和角度，然后用直方图统计，横着的为角度，竖着的是填写角度对应的强度，将特征图转最大角度，归一化

解决了角度差异问题！ 

 除了尺寸（尺度不变，DoG，缩放），视角（梯度变化压缩圈住），旋转（算梯度旋转归一化）问题解决以外，

还有光线问题，使得两张图不能直接比较

我们用描述符表示，很鲁棒

方法：比如将特征划分16个小区域，然后每个区域算梯度直方图，横轴为8个角度，上下左右对角线。然后16*8个向量组成描述符

分成16格匹配更精准

 如果左图是库里的，右图是待检验新图。新图提取的特征经过归一描述符后，如果确定与中间的相似？

通过对第一近邻和第二近邻的比值，如果与两个相差不大则不要。