【无标题】

• 论文：https://arxiv.org/pdf/2410.04343
• 代码：未开源
• 机构：Google
• 领域：RAG
• 发表：arxiv

研究背景

1. 研究问题：这篇文章研究了长上下文检索增强生成（RAG）中的推理扩展问题，特别是如何通过增加推理计算来提高RAG的性能。
2. 研究难点：该问题的研究难点包括：如何在增加知识量的同时有效利用这些知识，以及如何在不增加上下文长度的情况下提高性能。
3. 相关工作：相关研究主要集中在通过增加检索文档的数量或长度来扩展RAG的知识量，但这些方法在处理复杂查询时存在局限性。

研究的贡献如下：
        系统地研究了长上下文 RAG 的推理扩展，为此引入了两种扩展策略 DRAG 和 IterDRAG，以有效地扩展推理计算。
        • 全面评估了 DRAG 和 IterDRAG，它们不仅实现了最先进的性能，而且与单纯增加文档数量相比，还表现出卓越的扩展特性。
        • 在基准 QA 数据集上进行大量实验，证明了当测试时间计算得到最佳分配时，长上下文 RAG 性能可以随着计算预算数量级的增加而几乎线性地扩展。
        • 定量模拟了 RAG 性能与不同推理参数之间的关系，从而得出了计算分配模型。该模型与实验结果非常吻合，并且在各种场景中具有很好的泛化性，为长上下文 RAG 中的最佳计算分配提供了实用指导。

研究方法

这篇论文提出了两种推理扩展策略：演示基础RAG（DRAG）和迭代演示基础RAG（IterDRAG），用于解决长上下文RAG中的推理扩展问题。具体来说，

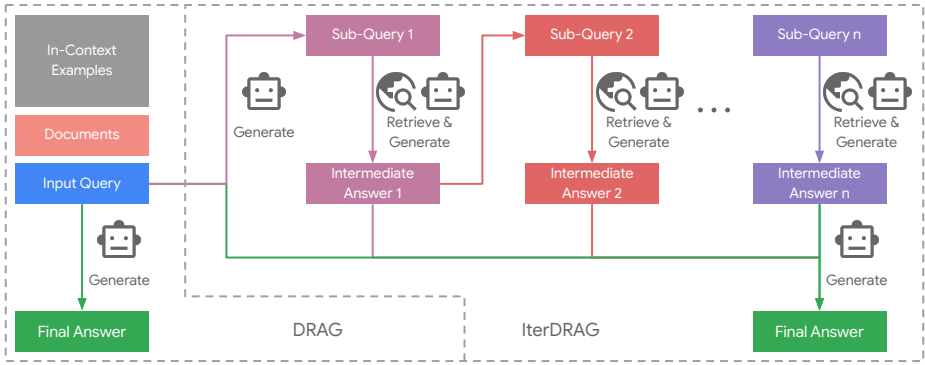
1. 演示基础RAG（DRAG）：DRAG通过将多个RAG示例作为演示提供给长上下文LLM，使其能够在单个推理请求中生成答案。DRAG的输入提示包括文档和上下文示例，扩展了上下文长度以允许模型在单个请求中回答问题。

2. 

   

3. 迭代演示基础RAG（IterDRAG）：IterDRAG通过将输入查询分解为更简单的子查询并使用交错检索来回答这些问题，从而处理复杂的多跳查询。IterDRAG在每次迭代中生成子查询、中间答案或最终答案，直到生成最终答案或达到最大迭代次数。

4. 

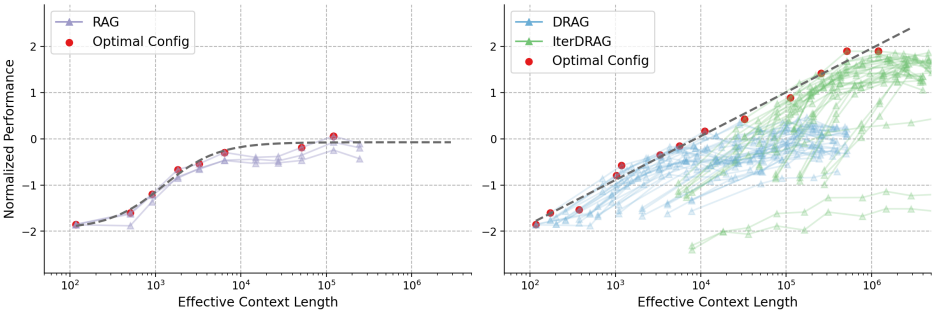
推理扩展定律：通过广泛的实验，作者发现RAG性能随着有效上下文长度的增加而近似线性增长，这一关系被称为RAG的推理扩展定律。 

实验设计

1. 数据集：实验使用了多个知识密集型问答数据集，包括Bamboogle、HotpotQA、MuSiQue和2WikiMultiHopQA。
2. 参数配置：对于DRAG，调整检索文档数量（k）和上下文示例数量（m）；对于IterDRAG，额外引入迭代次数（n）。
3. 评估指标：使用精确匹配（EM）、F1分数（F1）和准确率（Acc）作为评估指标。
4. 实验设置：在每个推理计算预算（如16k、32k、128k、1M和5M令牌）下，找到最优的平均指标（P∗(Lmax​)）。

在上下文长度不太长时(16-32k)，DRAG大于IterDRAG，而上下文非常长时(1M-5M)，IterRAG大于DRAG。

 

1. 推理扩展定律：RAG性能随着有效上下文长度的增加而近似线性增长，验证了推理扩展定律。

   

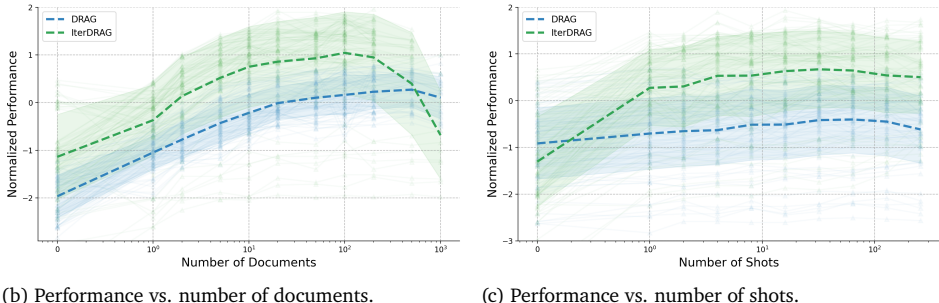
2. 参数特定扩展：增加文档、示例和迭代次数通常能提高性能，但每种参数的贡献不同。检索文档数量对性能的提升最为显著，而增加上下文示例对IterDRAG的帮助更大。

   

计算分配模型

总体结论

这篇论文系统研究了长上下文RAG中的推理扩展问题，提出了DRAG和IterDRAG两种策略，并通过广泛的实验验证了其有效性。推理扩展定律和计算分配模型为优化长上下文RAG的推理策略提供了坚实的基础。未来的研究可以进一步探索检索质量和长上下文建模的改进。