使用C++语言利用最小二乘拟合sin函数

---

一、前言

  给定一组正弦数据，我们希望能够利用最小二乘的思想对该组数据进行拟合，拟合公式为：
$$y=Asin(wx+\varphi )+b$$
  一般拟合分两种情况：

• 给定数据没有任何先验条件，需要直接根据给定的数据使用正弦函数进行拟合，这种情况的拟合是一种非线性的拟合，需要使用更高级的数学工具和优化算法，如遗传算法、粒子群优化、贝叶斯优化等；
• 给定数据已知它的角频率$w$，根据这个先验条件对给定的数据使用正弦函数进行拟合，这种情况拟合就比较简单了，可以使用最小二乘的方法。

  对于未给定角频率的情况，由于涉及更高级的算法，只用最小二乘没有办法很好的解决问题，所以接下来的讨论只针对第二种情况，已知一组数据它的角频率$w$。

---

二、最小二乘拟合sin曲线（数据）原理分析

  已知一组符合sin函数分布规律的数据：
$$(x_1,x_2,\dots ,x_n),(y_1,y_2,\dots ,y_n)$$

  我们知道，正弦曲线的一般形式是：$y=Asin(wx+\varphi )+b$，同时，他可以表示为$y=p_{1}sinwx+p_{2}coswx+p_3$，他们这些参数之间的对应关系为：
$$\begin{array}{c}\{\begin{array}{rl}A& =\sqrt{p_1^2+p_2^2}\\ \varphi & =arctan(\frac{p_2}{p_1})\\ b& =p_3\end{array}\end{array}$$
  我们的思路是先求出$p_1,p_2,p_3$，然后再根据公式（1）来计算$A,\varphi ,b$
  根据给定的数据建立以下方程组：
$$\begin{array}{c}\{\begin{array}{rl}{y}_1& =p_{1}sinw{x}_1+p_{2}cosw{x}_1+p_3\\ y_2& =p_{1}sinw{x}_2+p_{2}cosw{x}_2+p_3\\ & ⋮\\ y_n& =p_{1}sinw{x}_n+p_{2}cosw{x}_n+p_3\end{array}\end{array}$$
  我们将方程组（2）写成矩阵的形式：
$$\begin{array}{c}\left[\begin{array}{ccc}sinw{x}_1& cosw{x}_1& 1\\ sinw{x}_2& cosw{x}_2& 1\\ & ⋮& \\ sinw{x}_n& cosw{x}_n& 1\end{array}\right]\ast \left[\begin{array}{c}{p}_1\\ p_2\\ p_3\end{array}\right]=\left[\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_n\end{array}\right]\end{array}$$
  这样就变成了我们熟悉的问题：$Ax=b$，求解这类问题有许多现成的算法，这里我就不展开讨论，利用上述矩阵等式可以求解出参数$p_1,p_2,p_3$，进而求解出$A,\varphi ,b$

---

三、代码展示

#include <iostream>
#include <vector>
#include <cmath>
#include <Eigen/Dense> // 使用Eigen库进行矩阵计算
#define PI 3.1415926

using namespace std;
using namespace Eigen;

// 定义sin函数模型，A是振幅，omega是频率，phi是相位，b是偏移量
double sinFunc(double A, double omega, double phi, double b, double x) {
    return A * sin(omega * x + phi) + b;
}

// 最小二乘拟合sin函数
void fitSinCurve(const vector<double>& xData, const vector<double>& yData, double omega, double& A, double& phi, double& b) {
    int n = xData.size();
    MatrixXd AMatrix(n, 3);
    VectorXd bVector(n);
    
    // 构造系数矩阵和右侧向量
    for (int i = 0; i < n; i++) {
        AMatrix(i, 0) = sin(omega * xData[i]);
        AMatrix(i, 1) = cos(omega * xData[i]);
        AMatrix(i, 2) = 1.0;
        bVector(i) = yData[i];
    }
    
    // 使用最小二乘法计算拟合参数
    Vector3d params = AMatrix.colPivHouseholderQr().solve(bVector);
    
    A = sqrt(params(0) * params(0) + params(1) * params(1));
    phi = atan2(params(1), params(0));
    b = params(2); // 偏移量b
}

int main() {
    // 指定测试参数
    double true_A = 1.5;
    double true_omega = 2.0;
    double true_phi = PI / 4.0;
    double true_b = 0.5;

    // 生成一组测试数据
    vector<double> xData;
    vector<double> yData;
    for (double x = 0.0; x <= 10.0; x += 0.1) {
        double y = sinFunc(true_A, true_omega, true_phi, true_b, x);
        xData.push_back(x);
        yData.push_back(y);
    }

    // 执行sin函数拟合，拟合结果存储在以下变量中
    double fitted_A, fitted_phi, fitted_b;

    // 调用拟合函数
    fitSinCurve(xData, yData, true_omega, fitted_A, fitted_phi, fitted_b);

    // 输出拟合结果和指定的参数结果
    cout << "指定参数：" << endl;
    cout << "振幅 A: " << true_A << endl;
    cout << "角频率 omega: " << true_omega << endl;
    cout << "相位 phi: " << true_phi << endl;
    cout << "偏移量 b: " << true_b << endl;
    cout << "---------------------------" << endl;
    cout << "拟合结果：" << endl;
    cout << "振幅 A: " << fitted_A << endl;
    cout << "相位 phi: " << fitted_phi << endl;
    cout << "偏移量 b: " << fitted_b << endl;

    return 0;
}

结果如下所示：

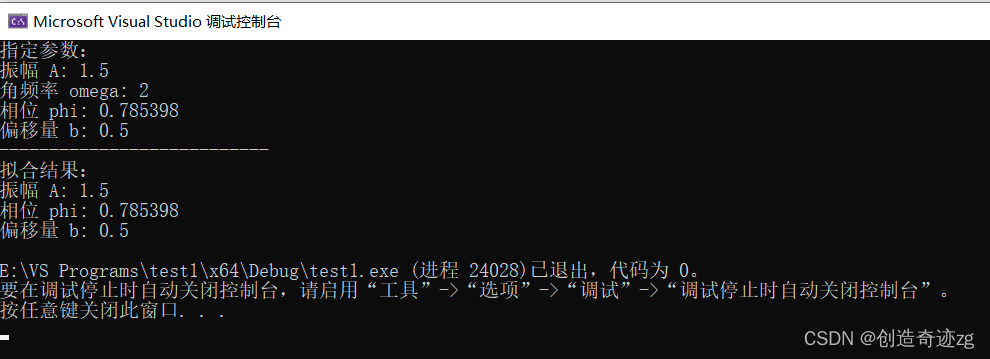
  可以看出，拟合结果与真实结果相同，为了检验该算法稳定性，我们可以在原始数据上添加噪声，代码如下：

高斯噪声生成函数

// 生成高斯随机数，用于生成噪声
// mu为均值，sigma为标准差
double generateGaussianNoise(double mu, double sigma) {
    static default_random_engine generator;
    normal_distribution<double> distribution(mu, sigma);
    return distribution(generator);
}

测试数据生成代码

double noise_mean = 0.0; // 噪声均值
double noise_stddev = 0.1; // 噪声标准差
for (double x = 0.0; x <= 10.0; x += 0.1) {
    double y_true = sinFunc(true_A, true_omega, true_phi, true_b, x);
    double y_noise = generateGaussianNoise(noise_mean, noise_stddev);
    double y = y_true + y_noise;
    xData.push_back(x);
    yData.push_back(y);
}

结果如下所示：

结果分析:
  通过上述结果可以看出，在添加一定的高斯噪声的情况下，该算法依旧可以很好地对数据进行拟合，效果还是非常好的。

---

四、总结

  以上拟合问题是在实际研究过程中遇到的问题，为了提高数据计算的精度，在网上看过许多拟合方法，但是都比较复杂，最终采用一种简单的方法来实现，希望对大家有所帮助和启发。如果大家还有什么想法，欢迎在评论区交流，有什么内容上或者其它的建议，也欢迎大家批评指出，谢谢。