提示:如果前面定理太复杂可以先看例题倒过来看
前言
小记一下,求解线性规划的单纯形法。
一、线性规划标准型
1.1标准型形式
形如:

称为线性规划问题的标准型
其中,
| 是 | |
| 为 | |
| 为 |
线性规划问题的理论和算法基本都是基于标准型得到的,实际出现的任何 线性规划问题都可以通过变换转为标准型。
(1)如果原问题是极大化目标函数,即。这时只需将目标函数乘以(−1), 则可等价地将其转化为极小化问题,
。
(2)如果右端项中的第
个元素是负的, 则在第i个约束方程两边同乘以−1,将其改 成右端项非负的不等式。
(3)若约束方程为≤不等式,则可在相应不等式的左端加上非负松弛变量,将原≤ 不等式变为等式。若约束方程为≥不等式,则可在相应不等式的左端减去非负剩余变量,将原≥不等式变为等式。(松弛变量和剩余变量没啥区别,就是名字不一样,个人感觉)
(4)如果某个变量是无非负限制的自由变量,则总可以引入两个非负变量
,
使 得
。
1.2标准型例题
将下面线性规划问题转化为标准型。

解:令,其中
。引入剩余变量
,引入松弛变量
,则标准型为

例题用到了处理方法(1)(2)(3)(4),实际情况中可能只用到其中一部分。
二、单纯形表格法
2.1相关概念和定义
将写成分块矩阵
,记
,
。
因此可以写成
得
再令,得到
的一个解
。
其中:
| 是矩阵 | |
| 是 |
基本解、可行解、基本可行解、最优基本可行解
| 基本解 | 基本可行解 | 最优基本可行解 | |||
| 可行解 | 最优可行解 | ||||
| 使 | |||||
2.2单纯形表法
单纯形表法的目标是求解最优基本可行解,形如:
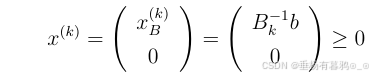
其中:为基矩阵,
为基变量。在
处的目标函数值为
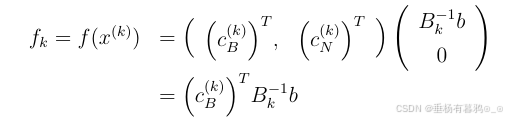
先对线性规划问题做等价变换,引入中间变量让线性规划问题的形式往最优可行解的形式靠近。
,记
,
则
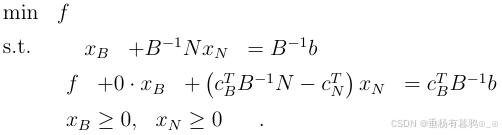
由上述约束方程系数得到如下单纯形表,其包含了单纯形方法所需要的所有数据。
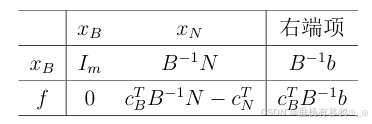
下面我们讨论如何用单纯形表求解标准线性规划问题。由于单纯形表中已经包含了m阶单位矩阵,因此已经给出了一个基本可行解。
记,其中
为非基本变量指标集(除去Im剩下的,就是xN下面对应的列)。我们称
为判别数或检验数。
(1)停机准则
若所有判别数都小于等于0,即,则现行基本可行解是最优解。
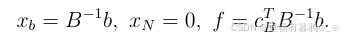
(2)改进基本可行解
若存在指标使得
我们需要进行主元消去法求解改进的基本可行解。由
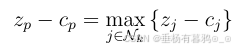
决定为进基变量,它所对应的列为主列。
再令由
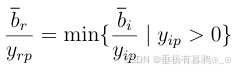
决定第行为主行。主行和主列交叉的元素
为主元。然后进行主元消去法, 使得主列化为单位列向量。
一般地,我们通过从原始变量、引入的松弛变量或人工变量选 取初始基变量,使得相应初始基矩阵为单位阵,即,然后计算初始的判别数得到初始单 纯形表。
2.3单纯形法例题
用单纯形方法求解下列线性规划问题:
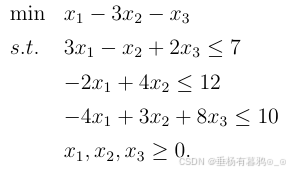
解:引入松弛变量转化为标准型:
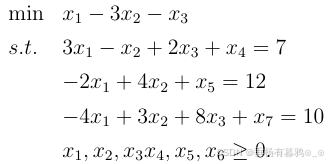
由标准型,可选取为基变量,建立单纯形表:
| 基变量 |
1 -3 -1 0 0 0 | |||
| | 0 0 0 | 3 -1 2 1 0 0 -2 4 0 0 1 0 -4 3 8 0 0 1 | 7 12 10 | 7/-1 12/4 10/3 |
| 0 0 0 0 0 0 | 0 | |||
| -1 3 1 0 0 0 | ||||
其中:,
=
,
=
由于,因此取第2列作为主列,
为进基变量。由于
,因此取第2行为主行,且x5为出基变量。主元为
,进行主元消去,将变量x2对应的列变换为单位列向量。新的基变量为x4,x2,x6。得到下表。
| 基变量 |
1 -3 -1 0 0 0 | |||
| | 0 -3 0 | 5/2 0 2 1 1/4 0 -1/2 1 0 0 1/4 0 -5/2 0 8 0 -3/4 1 | 10 3 1 | 10/2 1/8 |
| 1/2 -3 0 0 -3/4 0 | -9 | |||
| 1/2 0 1 0 -3/4 0 | ||||
由于,因此取第3列作为主列,
为进基变量。由于
,因此取第3行为主行,且x6为出基变量。主元为
,进行主元消去,将变量x3对应的列变换为单位列向量。新的基变量为x4,x2,x3。得到下表。
| 基变量 | 1 -3 -1 0 0 0 | |||
| | 0 -3 -1 | 8/25 0 0 1 7/16 -1/4 -1/2 1 0 0 1/4 0 -5/16 0 1 0 -3/32 1/8 | 39/4 3 1/8 | 78/25 |
| 29/16 -3 -1 0 -21/32 -1/8 | -73/8 | |||
| 13/16 0 0 0 -21/32 -1/8 | ||||
由于,因此取第1列作为主列,
为进基变量。由于
,因此取第1行为主行,且x4为出基变量。主元为
,进行主元消去,将变量x1对应的列变换为单位列向量。新的基变量为x,x2,x3。得到下表。
| 基变量 | 1 -3 -1 0 0 0 | |||
| | 1 -3 -1 | 1 0 0 8/25 7/50 -2/25 0 1 0 4/25 8/25 -1/25 0 0 1 1/10 -1/20 1/10 | 78/25 114/25 1/10 | |
| 1 -3 -1 -13/50 -77/100 -3/50 | -583/50 | |||
| 0 0 0 -13/50 -77/100 -3/50 | ||||
由于所有, 因此达到最优值,由单纯形表可知,所得到的最优值是
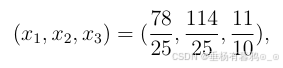
目标函数最优值
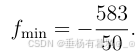
总结
好好努力!!!!





















 4360
4360

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








