回溯法实现最佳调度问题
- 掌握回溯法的深度优先搜索策略、剪枝策略及基本概念
- 掌握两种基本的解空间树:子集树和排列树
- 掌握装载问题、0-1背包问题、n后问题、旅行售货员问题。
- 掌握回溯法的效率分析。
- 算法设计题:使用回溯法实现最佳调度问题(P162,5-15) (需要文字描述解空间树的组织和限界函数的设计)。

分析:
我们知道回溯法其实是穷举法加剪枝函数,我们的函数用到递归,层层返回。一共七层,每层的除去叶子节点都有三个孩子
每搜索到叶子节点就更新一次best值(小于best则更新)(初值为一个较大的数),是用一次搜索结束后三个机器中花费时间最长的机器的所用时间作为此次分配的所用时间。
解空间树的组织:
问题的解空间描述了nk种可能性,如果k=3,那么每件任务都有3中选择,即解空间中每个结点有k个分支,称为k叉树。
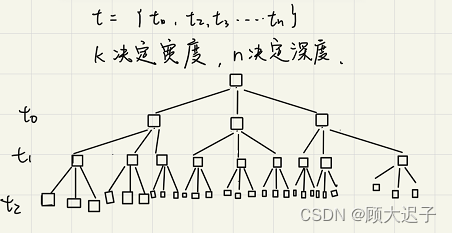
限界函数的设计:
如果时间上界大于当前搜索到的best,那么继续搜索不可能得到一个更优解,所以可以剪去。反之,则继续搜索
t[deep] + x[i] <= best
代码:
py:
# 打开input.txt文件
fr = open("input.txt", "r+")
temp = (fr.readline())
# temp返回str,注意k应该为temp[2]
n = int(temp[0])
k = int(temp[2])
t = fr.readline().split()
best = 100000
# 机器所用时间
x = [0] * (k + 1)
def __task(deep, y):
# 修改best全局变量
global best
if y > best: return
if deep >= n:
temp = 0
# 这个循环为了获得k个机器中用时最长作为总时长
for i in range(1, k + 1):
if x[i] > temp:
temp = x[i]
# 这里为了更新best的值从而得到所有情况中的最优解
if temp < best:
best = temp
else:
for i in range(1, k + 1):
if int(t[deep]) + x[i] <= best:
x[i] += int(t[deep])
__task(deep + 1, max(y, x[i]))
x[i] -= int(t[deep])
__task(0, 0)
print(best)
fw = open("output.txt", "w+")
fw.write(str(best))
c ++:
#include<bits/stdc++.h>
using namespace std;
int n,k;
int x[100];//机器
int x1[100];//作业
int maxnum=1000000;
void task(int level)
{
if(level>n){
int temp=0;
for(int i=1;i<=k;i++){
if(x[i]>temp){
temp=x[i];
}
}
if(temp<maxnum){
maxnum=temp;
}
}
else{
for(int i=1;i<=k;i++){
x[i]+=x1[level];
task(level+1);
x[i]-=x1[level];
}
}
}
int main()
{
cin >> n;
cin >> k;
for(int i=1;i<=n;i++){
cin >>x1[i];
}
task(1);
cout << maxnum;
return 0;
}回溯法和分支限界法的区别:
共同点:一种在问题的解空间树上搜索问题解的算法。
不同点:
- 求解目标不同,回溯法的目标是找出解空间树满足约束条件的所有解,而分支限界法的求解目标是尽快地找出满足约束条件的一个解;
- 搜索方法不同,回溯法采用深度优先方法搜索解空间,而分支限界法一般采用广度优先或以最小消耗优先的方式搜索解空间树;
- 对扩展结点的扩展方式不同,回溯法中,如果当前的扩展结点不能够再向纵深方向移动,则当前扩展结点就成为死结点,此时应回溯到最近一个活结点处,并使此活结点成为扩展结点。分支限界法中,每一次活结点只有一次机会成为扩展结点。活结点一旦成为扩展结点,就一次性产生其所有儿子结点;
- 存储空间的要求不同,分支限界法的存储空间比回溯法大得多,当内存容量有限时,回溯法成功的可能性更大。
























 6556
6556

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








