​支持向量回归

 支持向量回归

1、分类模型作回归

之前的章节里说过回归模型怎么去做分类，就是找到一个联系函数，将其化为0/1进行分类。若是本来是一个找线性分类的模型，如何做回归？

仔细思考，所谓回归不就是找一个超平面从样本点中穿过，穿的越近越好。通过上述分类来看，那我就找到一个超平面将所有的点都离我很近。如此一来不久达成回归了。

那么基本思路为：允许模型输出与实际输出存在2ϵ的差别，如图：

也就是说让中间靠近超平面的点不计损失，在间隔带以外的样本点计算损失，即

红线与z轴的两个交点分别是-ϵ和ϵ。很明显在(-ϵ,ϵ)区间内值为0，即无惩罚。距离这个交点越远，给予的惩罚就越多。希望得到的惩罚可以达到最小化，找到最小化以后就能找到最好。

2、支持向量回归(SVR)

支持向量机的优化问题可形式化为：

其中为"ϵ不敏感损失函数"（类比线性回归的均方误差损失）

为L2正则项，此处引入正则项除了起正则化本身的作用外，也是为了和软间隔支持向量机的优化目标保持形式上的一致，这样就可以导出对偶问题引入核函数，C为用来调节损失权重的正则化常数。

支持向量回归的做法和软间隔是非常相似的。引入松弛变量，令：

显然，并且当时，，当时，，所以

因此支持向量回归的优化问题可以化为

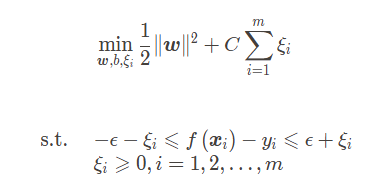
如果考虑两边采用不同的松弛变量，则有

PS5-1:SVR为啥要引入两个松弛变量？

就是你这个要看两边了，所以引入两个。

通过引入拉格朗日乘子，得到拉格朗日函数

令其对w，b，，的偏导为0，得：

再将其带回，得到SVR对偶问题：

上述过程中需满足KKT条件，即

PS5-2：推导过程

则SVR的解形如：

这里又有内积了，再用到核函数技巧，令 ,SVR就可以表示为：

3、如何使用SVM？

一定要把握好这个算法思想，SVM不是僵化的算法。

        入门级——实现并使用各种版本SVM

        专业级——尝试、组合核函数

        专家级——根据问题而设计目标函数、替代损失…..