二叉树理论基础
二叉树的种类:满二叉树和完全二叉树
满二叉树:如果一棵二叉树只有度为0的节点和度为2的节点,并且度为0的节点在同一层上,则这棵二叉树为满二叉树。深度为k,有2^k - 1个节点的二叉树。
完全二叉树:除了最底层节点没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。
二叉搜索树:一个有序树
- 若它的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
- 若它的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
- 它的左右子树也分别为二叉排序树。
平衡二叉搜索树
是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
C++中map、set、multimap、multiset的底层实现都是平衡二叉搜索树
二叉树的存储方式
二叉树可以链式存储,也可以顺序存储
链式存储就是用指针,顺序存储就是用数组。
二叉树的遍历方式
主要有两种遍历方式:
1.深度优先遍历:先往深走,遇到叶子节点再往回走
前序遍历,中序遍历,后序遍历
2.广度优先遍历:一层一层的去遍历
层次遍历(迭代法)
前中后序遍历指的就是中间节点的位置就可以了。
前序遍历:中左右;中序遍历:左中右;后序遍历:左右中
二叉树的定义
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL){}
}二叉树的递归遍历
递归三部曲
1.确定递归函数的参数和返回值
2.确定终止条件
3.确定单层递归的逻辑
以前序遍历为例:
1.确定递归函数的参数和返回值
void traversal(TreeNode* cur, vector<int>& vec)2.确定终止条件
if (cur == NULL) return;3.确定单层递归的逻辑
vec.push_back(cur->val);
traversal(cur->left,vec);
traversal(cur->right,vec);单层递归前序遍历:
//前序遍历
class Solution {
public:
void traversal(TreeNode* cur, vector<int>& vec) {
if (cur == NULL) return;
vec.push_back(cur->val);
traversal(cur->left, vec);
traversal(cur->right, vec);
}
vector<int> preorderTraversal(TreeNode* root) {
vector<int> result;
traversal(root, result);
return result;
}
};
//中序遍历
void traversal(TreeNode* cur, vector<int>& vec){
if (cur == NULL) return;
traversal(cur->left, vec);
vec.push_back(cur->val);//末尾添加元素
traversal(cur->right, vec);
}
//后序遍历
void traversal(TreeNode* cur, vector<int>& vec) {
if (cur == NULL) return;
traversal(cur->left, vec);
traversal(cur->right, vec);
vec.push_back(cur->val);
}
二叉树的迭代遍历
前序遍历(迭代法)
中左右,每次先处理的是中间节点,现将根节点放入栈中,然后将右孩子加入栈,再加入左孩子。
这样才能保证出栈的时候是中左右。
//迭代前序遍历
struct TreeNode:
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x): val(x), left(NULL), right(NULL){}
class Solution {
public:
vector<int> preordertraversal(TreeNode* root) {
//初始化二叉树栈,结果数组
stack<TreeNode*> st;
vector<int> result;
if (root == NULL) return result;
//root先入栈
st.push(root);
while(!st.empty()) {
TreeNode* node = st.top();
st.pop();
result.push_back(node->val);
//先入右再入左,才能顺序弹出左右
if (node->right) st.push(node->right);
if (node->left) st.push(node->left);
}
return result;
}
}
层序遍历
#include <iostream>
using namespace std;
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x):val(x), left(NULL), right(NULL) {}
}
//层序遍历是利用队列一层一层
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode *root) {
queue<TreeNode*> que;//队列中放的是指针
vector<vector<int>> result;
if (root == NULL) return result;
que.push(root);
while (!que.empty()) {
int size = que.size();//因为que.size一直在变,使用固定的size
vector<int> vec;//存储单层
//分层弹出
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
vec.push_back(node->val);
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
result.push_back(vec);
}
return result;
}
}自底向上层序遍历:
对result进行翻转即可
二叉树的右视图
思路:层序遍历的时候,判断是否遍历到单层的最后面的元素,如果是,就放进result数组中,随后返回result就可以了。
层平均值
思路:本题就是层序遍历的时候把一层求个总和再取一个均值。
N叉树遍历
思路:增加孩子节点
for(int i = 0; i < node->children.size(); i++) {
if (node->children[i]) que.push(node->children[i]);
}在每个树行找到最大值
思路:
maxValue = node->val > maxValue ? node->val : maxValue;class Solution {
public:
Node* connect(Node* root) {
queue<Node*> que;
if (root != NULL) que.push(root);
while(!que.empty()) {
int size = que.size();
Node* nodePre;
Node* node;
for(int i = 0; i < size; i++) {
if (i == 0) {
nodePre = que.front();//取出一层头结点
que.pop();
node = nodePre;
}else {
node = que.front();
que.pop();
nodePre->next = node;//本层前一个节点的next指向本节点
nodePre = nodePre->next;
}
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
nodePre->next = NULL;
}
return root;
}
};最大深度:记录层数
最小深度:
if(!node->left && !node->right) return depth;翻转二叉树
思路:只需要将每个节点的左右孩子翻转
1.确定递归函数的参数和返回值
参数就是要传入节点的指针,返回root节点的指针
TreeNode* invertTree(TreeNode* root)单层递归逻辑:
swap(root->left,root->right);
对称二叉树
1.确定递归函数的参数和返回值
因为要比较的是根节点的两个子树是否相互翻转,进而判断这个树是不是对称树,所以要比较的是两个树
2.确定终止条件,有空节点或者不相等就终止
3.确定单层递归逻辑
//比较外侧:左节点左孩子,右节点右孩子
//比较里侧:左节点右孩子,右节点左孩子
class Solution {
public:
//1.确定递归函数的参数和返回值
//因为要比较的是根节点的两个子树是否相互翻转,进而判断这个树是不是对称树,所以要比较的是两个树
bool compare(TreeNode* left, TreeNode* right) {
//2.确定终止条件,有空节点或者不相等就终止
if (left==NULL && right != NULL) return false;
else if (left!=NULL && right == NULL) return false;
else if (left == NULL && right == NULL) return true;
else if (left->val != right->val) return false;
//3.确定单层递归逻辑
//比较外侧:左节点左孩子,右节点右孩子
//比较里侧:左节点右孩子,右节点左孩子
bool Outside = compare(left->left->val == right->right->val);
bool Inside = compare(left->right->val == right->left->val);
bool isSame = outSide && OutSide;
return isSame;
}
bool isSymmertic(TreeNode* root) {
if (root == NULL) return true;
return compare(root->left, root->right);
}
};最大深度
关键在于:左右中
中:int depth = 1 + max(leftdepth, rightdepth);
//确定递归函数的参数和返回值
class Solution {
public:
int getdepth(TreeNode* node) {
//2.终止条件
if (node == nullptr) return 0;
//3.单层递归逻辑
int leftdepth = maxDepth(node->left);
int rightdepth = maxDepth(node->right);
//----------关键----------------------
int depth = 1 + max(leftdepth, rightdepth);
return depth;
}
int maxDepth(TreeNode* root) {
return getdepth(root);
}
};
最小深度
关键:

//防止没有左孩子或者右孩子分支会被算做最短深度
//左子树为空,右子树不空,最小深度是1+右子树深度
//右子树同理
class Solution {
public:
//确定递归函数的参数和返回值
int getdepth(TreeNode* node) {
//确定终止条件
if(node == nullptr) return 0;
//单层递归逻辑
int leftdepth = getdepth(node->left);
int rightdepth = getdepth(node->right);
//防止没有左孩子或者右孩子分支会被算做最短深度
//左子树为空,右子树不空,最小深度是1+右子树深度
//右子树同理
if (node->left == nullptr && node->right != nullptr){
return 1 + rightdepth;
}
if (node->left != nullptr && node->right == nullptr) {
return 1 + leftdepth;
}
int depth = 1 + min(leftdepth, rightdepth);
return depth;
}
int minDepth(TreeNode* root) {
return getdepth(root);
}
};完全二叉树的节点个数
完全二叉树:除了最后一层没满,其他层都是满的,最后一层的节点都集中在最左边。
关键:左右中
中: int Sum = 1 + leftNodeSum + rightNodeSum;
class Solution {
public:
int getNodeSum(TreeNode* cur) {
if (cur == nullptr) return 0;
//确定单层递归逻辑
int leftNodeSum = getNodeSum(cur->left);
int rightNodeSum = getNodeSum(cur->right);
int Sum = 1 + leftNodeSum + rightNodeSum;
return Sum;
}
int countNodes(TreeNode* root) {
return getNodeSum(root);
}
};
平衡二叉树
思路要多看
定义:一个二叉树每个节点的左右两个子树的高度差的绝对值不超过1
与最大深度不同,这是求最大高度。
关键:左节点调用递归后,如果为空就是-1,右节点也是,然后再相减获得大小差值。
否则就是result = 1 + max(leftHeight, rightHeight)
class Solution {
public:
int getHeight(TreeNode* node) {
if (node == nullptr) return 0;
int leftHeight = getHeight(node->left);
if (leftHeight == -1) return -1;
int rightHeight = getHeight(node->right);
if (rightHeight == -1) return -1;
int result;
if (abs(leftHeight - rightHeight) > 1) {
return -1;
} else {
result = 1 + max(leftHeight, rightHeight);
}
return result;
}
bool isBalanced(TreeNode* root) {
return getHeight(root) == -1 ? false : true;
}
};二叉树的所有路径
思路捋清楚了,防止忘记
1.确定递归函数的参数和返回值
根节点,路径,存储路径的结果
2.确定终止条件
终止条件的逻辑:找到叶子节点,遍历path,把path转成字符串保存到result中
3.单层递归逻辑
左+回溯
右+回溯
class Solution {
public:
//1.确定递归函数的参数和返回值
//根节点,路径,保存路径的结果
void traversal(TreeNode* cur, vector<int>& path, vector<string>& result) {
//中
path.push_back(cur->val);
//2.确定终止条件
//找到叶子节点
if (cur->left == NULL && cur->right == NULL) {
//确定终止逻辑
//把路径遍历出来
string sPath;
for (int i = 0; i < path.size() - 1; i++) {
sPath += to_string(path[i]);
sPath += "->";
}
sPath += to_string(path[path.size() - 1]);
result.push_back(sPath);
}
//3.确定单层递归逻辑+回溯
if (cur->left) {
traversal(cur->left, path, result);
path.pop_back();
}
if (cur->right) {
traversal(cur->right, path, result);
path.pop_back();
}
}
vector<string> binaryTreePaths(TreeNode* root) {
vector<int> path;
vector<string> result;
traversal(root, path, result);
return result;
}
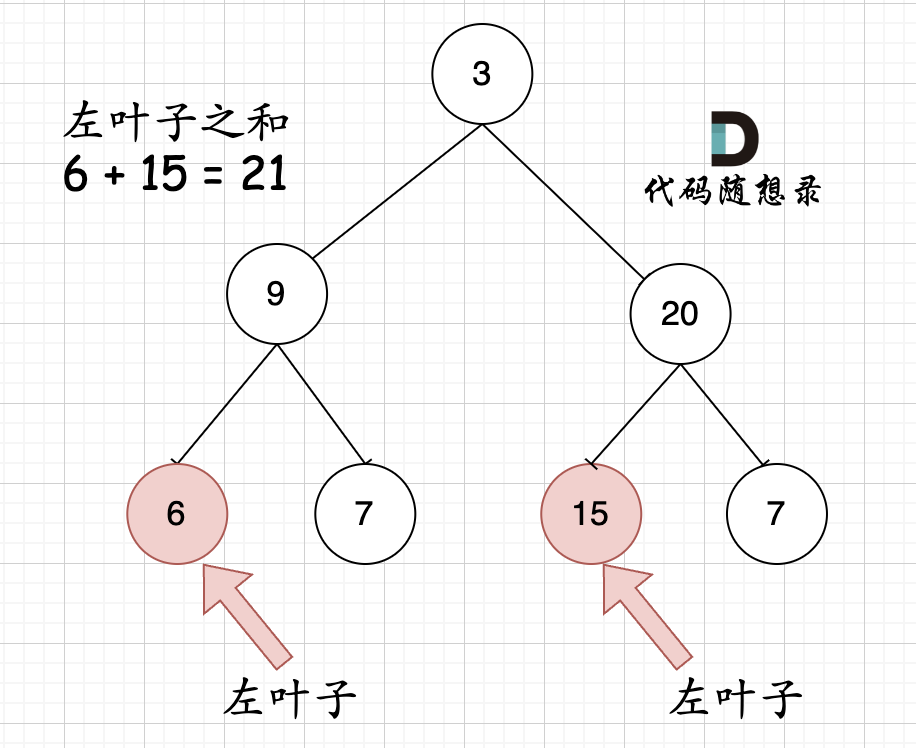
};左叶子之和
后序遍历,左右,和返回中。
关键:什么是左叶子:该节点的左孩子不为空,该节点的左孩子的左孩子为空,该节点的左孩子的右孩子为空。所以需要从父节点就判断
找到叶子节点,只能说明是叶子,无法判断是左叶子,返回只代表该叶子节点的左右树的和,因为是空,所以返回0.
class Solution {
public:
//1.确定递归函数的参数和返回值
//后续遍历
int leftsum(TreeNode* node) {
if (node == nullptr) return 0;
if (node->left==nullptr && node->right==nullptr) return 0;//找到叶子节点只能说返回左子树和右子树之和
int leftValue = leftsum(node->left);
//左叶子:该节点的左节点不为空,该节点的左节点的左节点为空,该节点的左节点的右节点为空
if (node->left!=nullptr && node->left->left==nullptr && node->left->right==nullptr){
leftValue = node->left->val;
}
int rightValue = leftsum(node->right);
int sum = leftValue + rightValue;
return sum;
}
};找到左下角的值
给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。
假设二叉树中至少有一个节点。
思路:层序遍历,记录i=0时候的值,每层遍历的时候都会刷新,直到最后一层。
注意:queue<TreeNode*> que; 这里是建立的二叉树指针型队列
在遍历中,建立二叉树TreeNode* node = que.front; 一直采用node进行遍历
class Solution {
public:
int findBottomLeftValue(TreeNode* root) {
queue<TreeNode*> que;
if (root != nullptr) que.push(root);
int result = 0;//记录那个节点
while (!que.empty()) {
int size = que.size();
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
if (i == 0) result = node->val;
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
}
return result;
}
};路径总和
给定一个二叉树和一个目标和,判断该树中是否存在根节点到叶子节点的路径,这条路径上所有节点值相加等于目标和。
说明: 叶子节点是指没有子节点的节点。
示例: 给定如下二叉树,以及目标和 sum = 22

返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。
思路:比求所有路径要简单。
确定终止条件:到达叶子节点且count=0,true;到达叶子节点且count不为0,false
单层递归逻辑:count减去节点值,回溯再加回来。
关键,traversal有返回值,所以单层逻辑中要写出返回值 if(traversal) return true
class Solution {
public:
//确定函数的参数和返回值
//根节点和计数值
bool traversal(TreeNode* cur, int count) {
//确定终止条件
//到达叶子结点且count为0,则true;不为0,则false
if (cur->left == nullptr && cur->right == nullptr && count == 0) return true;
if (cur->left == nullptr && cur->right == nullptr && count != 0) return false;
//单层递归逻辑+回溯
if (cur->left) {
count -= cur->left->val;
if (traversal(cur->left, count)) return true;
count += cur->left->val;
}
if (cur->right) {
count -= cur->right->val;
if (traversal(cur->right, count)) return true;
count += cur->right->val;
}
return false;
}
bool hasPathSum(TreeNode* root, int targetSum) {
if (root == nullptr) return false;
return traversal(root, targetSum - root->val);
}
};从中序和后序遍历序列构造二叉树

思路:
首先根据后序找到根节点的值,创建二叉树,将根节点写入
在中序中找到根节点值的索引,进行分割,
再对后序分割:先去掉最后一个用过的节点,由于左中序和左后序相等,则利用这个进行分割后序。
class Solution {
private:
TreeNode* traversal(vector<int>& inorder, vector<int>& postorder) {
if (postorder.size() == 0) return nullptr;
//在后序获取根节点
int rootVal = postorder[postorder.size() - 1];
TreeNode* root = new TreeNode(rootVal);
//在中序找到分割点索引
int splitIndex;
for (splitIndex = 0; splitIndex < inorder.size(); splitIndex++) {
if (inorder[splitIndex] == rootVal) break;
}
//分割中序
vector<int> leftinorder(inorder.begin(), inorder.begin() + splitIndex);
vector<int> rightinorder(inorder.begin() + splitIndex + 1, inorder.end());
//分割后序
//先将后序的最后一个节点整理掉
postorder.resize(postorder.size() - 1);
//左中序长度和左后序相等
vector<int> leftpostorder(postorder.begin(), postorder.begin() + leftinorder.size());
vector<int> rightpostorder(postorder.begin() + leftinorder.size(), postorder.end());
//单层递归逻辑
root->left = traversal(leftinorder, leftpostorder);
root->right = traversal(rightinorder, rightpostorder);
return root;
}
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
if (inorder.size() == 0 || postorder.size() == 0) return nullptr;
return traversal(inorder, postorder);
}
};最大二叉树
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
- 创建一个根节点,其值为
nums中的最大值。 - 递归地在最大值 左边 的 子数组前缀上 构建左子树。
- 递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树 。
思路:因为要考虑分割后的数组大于0,所以只有一个的时候就直接设置叶子结点
找最大值,最大值索引;
判断左二叉树是否大于0,分割,递归
判断右二叉树是否大于0,分割,递归
class Solution {
private:
TreeNode* traversal(vector<int>& nums) {
//题目>=1,只考虑叶子结点
TreeNode* node = new TreeNode(0);
if (nums.size() == 1) {
node->val = nums[0];
return node;
}
int maxVal = INT_MIN;
int maxValIndex = 0;
for (int i = 0; i < nums.size(); i++) {
if (nums[i] > maxVal) {
maxVal = nums[i];
maxValIndex = i;
}
}
node->val = maxVal;
//保证左区间最少有一个数值
if (maxValIndex > 0) {
vector<int> leftnode(nums.begin(), nums.begin() + maxValIndex);
node->left = traversal(leftnode);
}
//确保右子树至少有一个数值
if (maxValIndex < (nums.size() - 1)) {
vector<int> rightnode(nums.begin() + maxValIndex + 1, nums.end());
node->right = traversal(rightnode);
}
return node;
}
public:
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
return traversal(nums);
}
};






















 3657
3657

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








