本文深入探讨了强化学习中的策略学习，特别是策略网络π(a|s;θ)的运用。通过神经网络近似策略函数，形成一个5*10的概率表格来表示不同状态和动作的概率。同时，介绍了如何用近似的V函数评估状态和策略，并通过策略梯度算法优化网络参数，以达到最大化V函数的目的。文章还讨论了对于离散和连续动作的处理方式，以及在无法直接积分时采用蒙特卡罗近似的策略。
强化学习三 || 策略学习
策略函数 π(a|s)，它的输入是状态s，输出是一个概率分布，给每一个动作a一个概率值，如下图，就会输出一个三维向量，这三个动作都有可能被抽到，只不过概率有大有小
假如一个游戏只有5个状态，10个动作，我们画一张 5*10的表，表里面每一个格子表示一个概率
我们用神经网络来近似π函数，称之为策略网络 π(a|s;θ)
回顾一下 V 函数
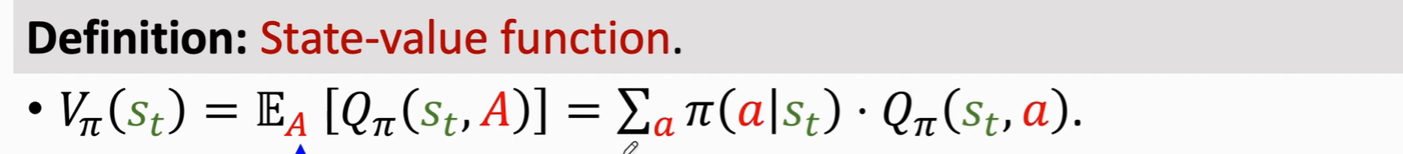
现在我们用神经网络来近似V函数，其实就是用近似的π函数来代替原公式的π函数
V函数可以评估状态s 和策略 π的好坏
我们再在V函数中对 s 求期望消掉 s ，得到 J(Θ) 对 J(Θ) 用策略梯度算法来求最优值
策略梯度算法
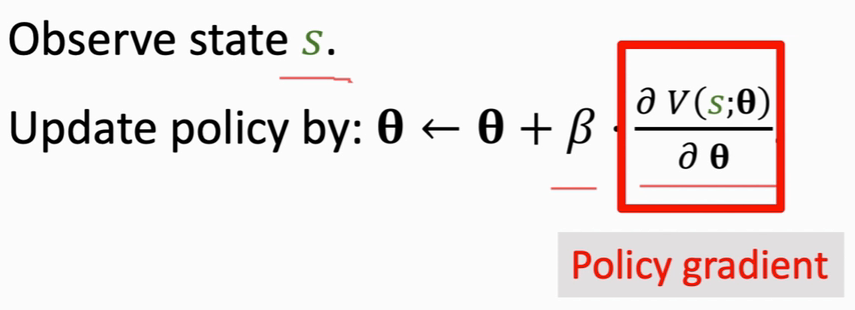
这是一个梯度上升算法，β是学习率
推导公式
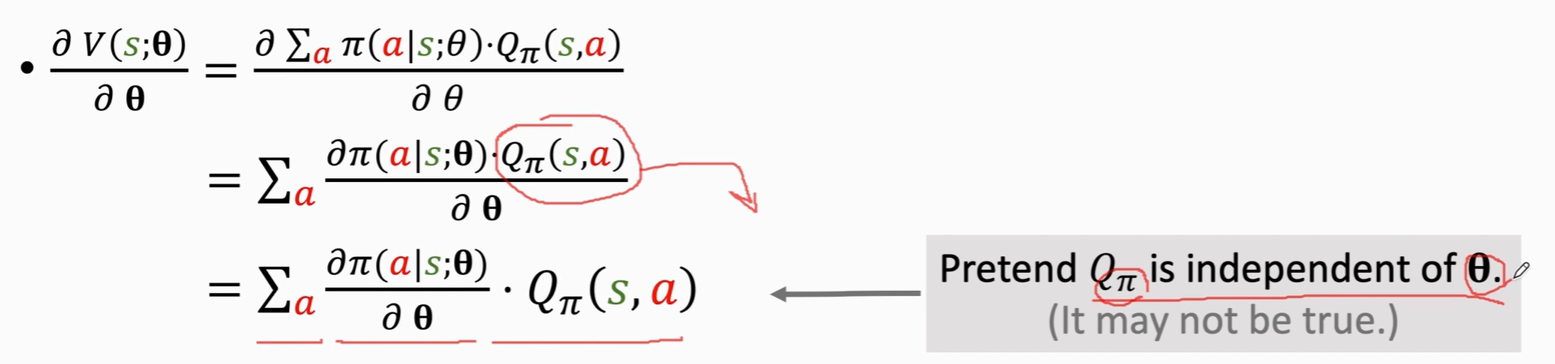
对于离散的动作——采用累加的方式
对于连续的动作——采用积分的方式
由于π函数是一个神经网络，参数较多，无法直接做积分；所以我们采用蒙克卡罗近似（用一个或多个随机样本来近似期望）来 得到该积分的近似值
从π函数中随机抽出一个动作 a_pred
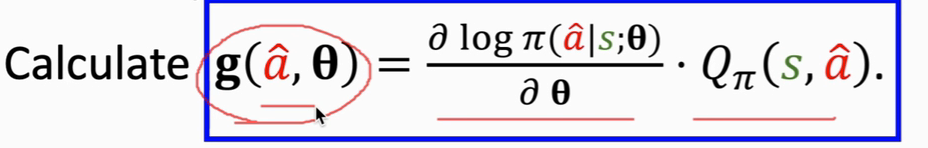
算出 g(a_pred,Θ)的值 ，这个值就是 无偏估计
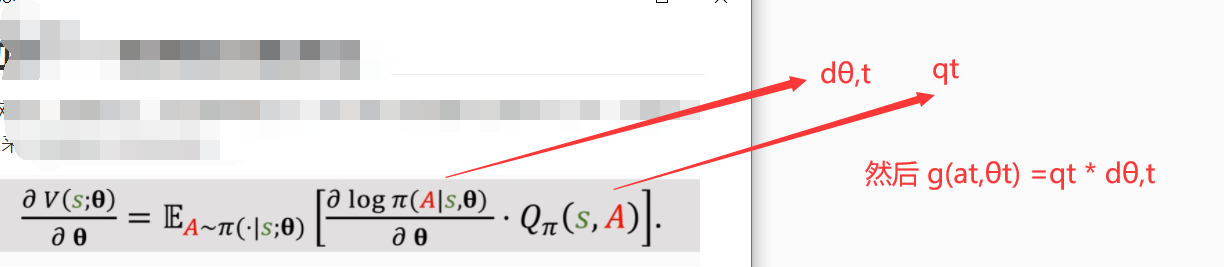
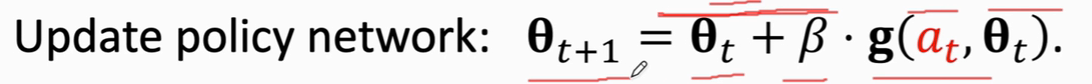
采用梯度上升，目的让 V函数变大
总结
扫一扫
1086
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
