【机器学习实验五】逻辑斯蒂回归

目录

一、逻辑斯蒂回归基本概念

1.1、基本概念

1.2、特点

1.3、Logistic分布

1.4、逻辑斯蒂回归模型

 二、利用逻辑斯蒂模型进行分类测试

2.1、数据准备

2.2、编写代码查看数据集的分布情况

2.3、训练分类算法

2.4、绘制决策边界

三、从疝气病症状预测病马的死亡率 

3.1、项目背景

3.2、数据准备

3.3、使用Python构建logistics分类器

四、总结

4.1、Logistic回归的一般过程：

4.2、优缺点

---

一、逻辑斯蒂回归基本概念

1.1、基本概念

逻辑斯蒂（Logistic）回归又称为“对数几率回归”，虽然名字有回归，但是实际上却是一种经典的分类方法，其主要思想是：根据现有数据对分类边界线（Decision Boundary）建立回归公式，以此进行分类。

 1.2、特点

• 优点：计算代价不高，具有可解释性，易于实现。不仅可以预测出类别，而且可以得到近似概率预测，对许多需要利用概率辅助决策的任务很有用。
• 缺点：容易欠拟合，分类精度可能不高。
• 适用数据类型：数值型和标称型数据。

1.3、Logistic分布

Logistic 分布是一种连续型的概率分布，其分布函数和密度函数分别为：

其中，μ 表示位置参数，γ 为形状参数。我们可以看下逻辑斯蒂分布在不同的、的情况下，其概率密度函数的图形：

               

 逻辑斯蒂分布在不同的、的情况下，其概率分布函数的图形：

             

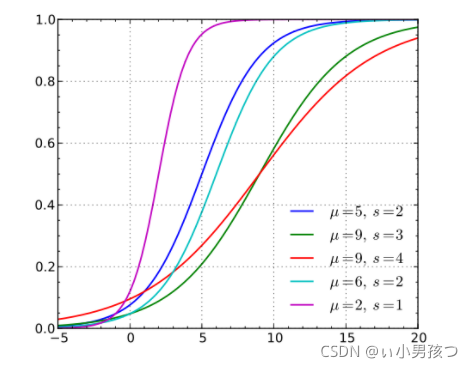
 Logistic 分布是由其位置和尺度参数定义的连续分布。Logistic 分布的形状与正态分布的形状相似，但是 Logistic 分布的尾部更长，所以我们可以使用 Logistic 分布来建模比正态分布具有更长尾部和更高波峰的数据分布。在深度学习中常用到的 Sigmoid 函数就是 Logistic 的分布函数在μ=0,γ=1 的特殊形式。

1.4、逻辑斯蒂回归模型

逻辑斯蒂回归模型是一种分类模型，由条件概率分布P(Y|X)表示，形式为参数化的逻辑斯蒂分布。这里随机变量X取值为实数，随机变量Y取值为1或0。

二项逻辑斯谛回归模型是如下的条件概率分布：

                                  

这里x属于实数，Y属于{0,1}是输出，w和b是参数，w称为权值向量，b称为偏置，w*x为w和x的内积。

对于给定的输入实例x，按照上述分布函数可以求得P(Y=1|x)和P(Y=0|x)。逻辑斯谛回归是比较两个条件概率值的大小，将实例x分到概率值大的那一类。

有时候为了方便，将权值向量和输入向量加以扩充，仍记作w,x，即

                      

 这时，逻辑斯蒂回归模型如下：

                              

 得到上面的回归模型了，上面的回归模型中有一个未知参数w，在利用上述的模型对数据进行预测之前需要先求取参数w的值，这里采用极大似然估计的方法求取参数w。

假设：

                                             

                                         

 可以得到似然函数为：

                                       

 对似然函数取对数可得：

这样问题就变成了以对数似然函数为目标函数的最优化问题。逻辑斯蒂回归学习中通常采用的方法是梯度下降法或者梯度上升法。

将利用极大似然估计得到的w值代入上述的模型中，即可用于测试数据集的预测。

 二、利用逻辑斯蒂模型进行分类测试

2.1、数据准备

 如图所示，该数据有两个特征维度，我们可以将第一列看作x轴的值，第二列看作y轴的值，第三列为分类的标签。