多维度卷积运算精髓

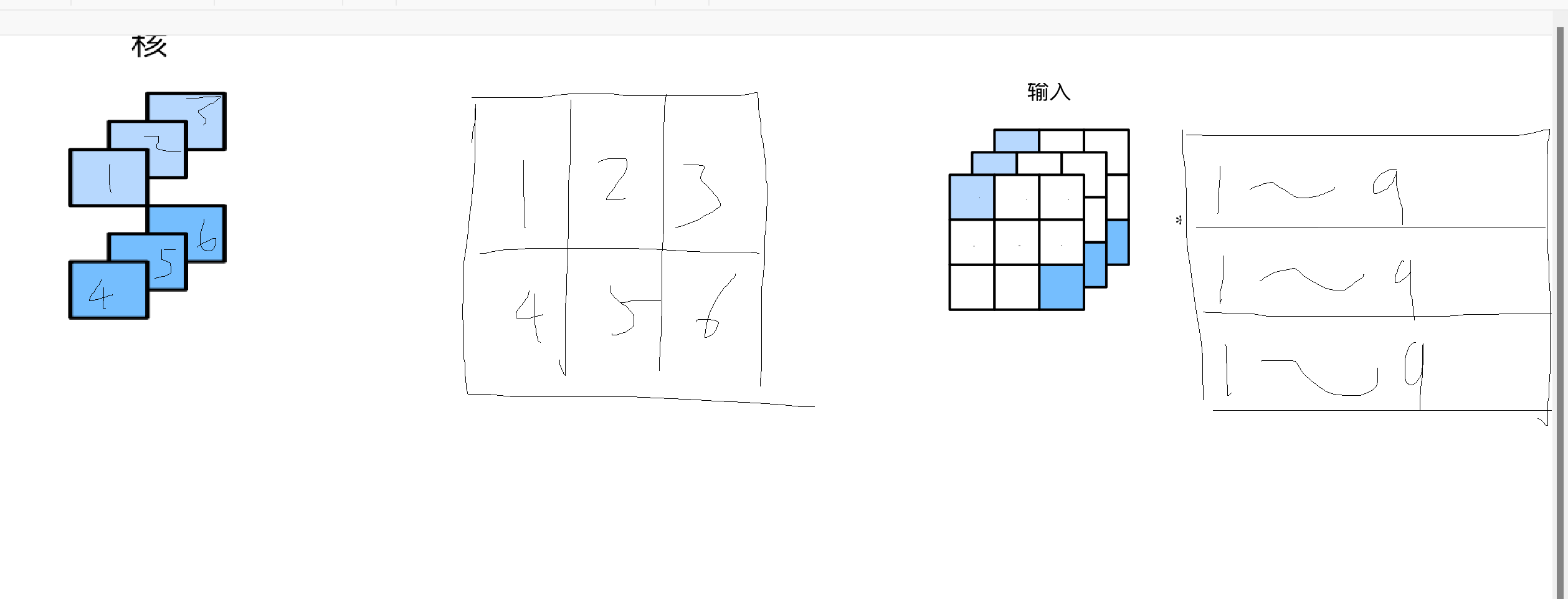
卷积运算的精髓在于每一个卷积层的卷积核的维度，特别是多维度的情况下，我们在思考多维度的卷积运算的时候，我们需要先搞明白假如卷积核为（c1,c2,1,1）的这种维度下的情况是如何的？

每一层的卷积核为1维的情况下，这种情况是如何计算的？

请看上图，如图所示，我已经把2*3*1*1的卷积核展开，分别先按照输出通道维数，输入通道维数，接着1*1的矩阵数字展开成一个2维的矩阵，在这种情况下，我们接着把输入数据展开，分别按照输入通道维数，还有每个矩阵按照行和列展开成一个1行的数列，那么这种情况下，我们可以按照如下代码进行乘法运算：

def corr2d_multi_in_out_1x1(X, K):

c_i, h, w = X.shape

c_o = K.shape[0]

X = X.reshape((c_i, h * w))

K = K.reshape((c_o, c_i))

Y = nd.dot(K, X) # 全连接层的矩阵乘法

return Y.reshape((c_o, h, w))

这种情况下，我们就可以让卷积核与输入数据进行矩阵乘法运算，也就是dot运算，最后我们把得出的结果进行重新捏形状，直接就可以变成最终新的矩阵，实例如下：

X = nd.random.uniform(shape=(3, 3, 3))

K = nd.random.uniform(shape=(2, 3, 1, 1))

Y1 = corr2d_multi_in_out_1x1(X, K)

Y1

[[[1.6569827 0.86790574 0.674144 ]

[1.8918769 1.0956942 0.34890684]

[1.2571611 1.3171167 1.7891276 ]]

[[0.69264996 0.43731803 0.18686524]

[0.89936227 0.48084605 0.19427292]

[0.51245344 0.53381854 0.80302143]]]

<NDArray 2x3x3 @cpu(0)>

还有一点特别需要注意的是，我们在定义输入数据的时候，输入数据的高和宽不需要一定和卷积核的高和宽一样，但是输入通道的数目一定要一致。而且看到这里，想必能看出来，我们在定义一个高和宽是1*1的卷积核的时候，会出现输出数据的高和宽不变的情况，那么这种情况是有什么用呢？

1. 当高和宽都是1的时候，我们可以更好的控制模型复杂度，我们不会导致输出数据的形状改变，这个在神经网络前向传播过程中是非常有用的。

2. 而且这种卷积核可以等价与全连接神经网络的矩阵运算，可以把卷积核的通道维当成特征维，因为我们发现，当进行维度是1的2维互相关运算的时候，我们发现只是需要按照卷积窗口大小，让输入数据跟卷积核进行对应位置元素的相乘再相加，那么如果是3个通道的卷积核跟3个通道的输入数据进行运算的时候，我们会发现第一个通道的卷积核跟第一个通道的第一个卷积窗口的数组进行简单乘法加和，然后第二个通道的卷积核跟第二个通道的第一个卷积窗口的乘法加和，第三个通道的卷积核跟第三个通道的第一个卷积窗口的矩阵进行乘法加和，最后再把这三个数字加起来形成输出矩阵的第一个元素，那么我们再回头思考，如果是这种情况的话，我们是否可以把每个通道的1*1的卷积核的数字按照特征值放在第一个通道，第二个通道，第三个通道，这样我们就可以回归到全连接层的矩阵运算方法了

3. 当我们进行某个多层神经网络运算过程中，我们需要在中间进行缩小输出数据的通道数目，但是不想改变高和宽的情况下，我们就需要用到这种1*1的卷积核的方式了，

可以进一步思考，那如果不是1*1的卷积核的方法呢？ 我们如何展开，依然是一个道理，我们可以按照上述展开卷积核为2维数组的方式去展开，这样运算会加快很多，那么接下来给出一个另类方法，计算多通道的卷积运算。

def corr2d_multi_in(X, K):

# ⾸先沿着X和K的第0维（通道维）遍历。然后使⽤*将结果列表变成add_n函数的位置参数

# （positional argument）来进⾏相加

return nd.add_n(*[d2l.corr2d(x, k) for x, k in zip(X, K)])

def corr2d_multi_in_out(X, K):

# 对K的第0维遍历，每次同输⼊X做互相关计算。所有结果使⽤stack函数合并在⼀起

return nd.stack(*[corr2d_multi_in(X, k) for k in K])

K = nd.stack(K, K + 1, K + 2)

corr2d_multi_in_out(X, K)

out:

[[[ 56. 72.]

[104. 120.]]

[[ 76. 100.]

[148. 172.]]

[[ 96. 128.]

[192. 224.]]]

<NDArray 3x2x2 @cpu(0)>