数据科学导引课程报告

最新推荐文章于 2022-10-10 23:49:24 发布

网路末端遗传因子

最新推荐文章于 2022-10-10 23:49:24 发布

阅读量1.1k

点赞数 2

文章标签： python 算法决策树

本文链接：https://blog.youkuaiyun.com/qq_54394719/article/details/118699705

版权

Q1:

公共自行车租借预测
自行车分享系统(bike sharing systems)较传统的自行车租借存在巨大的优势.它避免了注册、租借和归还等繁琐的过程，用户可以在线上完成所有相关操作.同时，自行车的行驶时长和路线等信息也可
以完整记录下来.
本题提供一份公共自行车租借数据集[36].请根据城市当天的天气、温度、湿度和风速等环境信息对自行车的租借数量进行预测.

Q2：

个人信用风险评估
在很多国家，政府机构会密切监控货款业务，银行需要明确解释申请者的贷款申请被拒绝或者批准的原因，这种可解释性对于贷款申请者也是很重要的，在贷款申请被银行拒绝时，申请者需要知道为什么自己的信用级别不符合银行的要求.
为什么自己的信用级别不符合银行的要求.

通过构建自动化的信用评分模型，以在线方式进行即时的信贷审批能够为银行节约很多人工成本.

数据集共有1000个贷款样本，每个样本包含20个相关特征和1个表示贷款是否违约的特征"default”．本章我们介绍的逻辑回归和决策树模型具有很好的可解释性.

请使用逻辑回归或者决策树算法建立个人信用风险评估模型.

Q3:

到了夏天,女士们热爱裙装.不同的款式和颜色搭配,可以让女士穿出不一样的风采,透出与众不同的魅力,本案例的数据集包含了裙装的款式,用料,颜色,大小，价格等方面的信息、销售人员可以根据这些信息，决定是否把某个具体型号的裙装推荐给客户,数据集一共有14个特征，501个样本.

本题要求依据裙装数据集，使用高斯混合模型对是否推荐裙装做判别.由于数据集特征均为名义型特征,需要对数据集作数据预处理,如特征编码等.

A1:

利用最小二乘法进行拟合，以此来做多元线性回归。通过得到线性回归的系数，来构建多元回归方程，从而将预测的数据代入自变量以后进行预测。

具体来说是：首先进行数据预处理，将离散型数据转化为one-hot编码，再进行OLS的拟合，将拟合的系数取出，构建方程，即可预测想要的数据。

这个是hour.csv的结果

==============================================================================

coef std err t P>|t| [0.025 0.975]

------------------------------------------------------------------------------

Intercept 3642.5000 433.334 8.406 0.000 2791.148 4493.852

temp 3228.9000 2454.526 1.315 0.189 -1593.395 8051.195

atemp 3623.0118 2770.730 1.308 0.192 -1820.514 9066.537

hum -2714.7015 468.416 -5.795 0.000 -3634.978 -1794.425

windspeed -3990.7544 865.630 -4.610 0.000 -5691.419 -2290.090

==============================================================================

Omnibus: 7.532 Durbin-Watson: 0.455

Prob(Omnibus): 0.023 Jarque-Bera (JB): 5.772

Skew: 0.153 Prob(JB): 0.0558

Kurtosis: 2.580 Cond. No. 81.7

这个是day.csv的结果

==============================================================================

coef std err t P>|t| [0.025 0.975]

------------------------------------------------------------------------------

Intercept 3642.5000 433.334 8.406 0.000 2791.148 4493.852

temp 3228.9000 2454.526 1.315 0.189 -1593.395 8051.195

atemp 3623.0118 2770.730 1.308 0.192 -1820.514 9066.537

hum -2714.7015 468.416 -5.795 0.000 -3634.978 -1794.425

windspeed -3990.7544 865.630 -4.610 0.000 -5691.419 -2290.090

==============================================================================

Omnibus: 7.532 Durbin-Watson: 0.455

Prob(Omnibus): 0.023 Jarque-Bera (JB): 5.772

Skew: 0.153 Prob(JB): 0.0558

Kurtosis: 2.580 Cond. No. 81.7

A2：对应Q2的算法

利用决策树C4.5的方法进行计算。通过选取最优特征来构建决策树，而最优特征的选取也取决于信息增益率，即信息增益除以当前根节点的信息熵。

由于数据中含有缺失值，以及连续型数值，所以无法使用ID3算法。而且也无法使用函数包进行计算，所以这里需要自己调用写好的C4.5针对性算法。

具体过程：将缺省值替换为我的C4.5可以检测到的值，并且对数据插入一列权值，使得我的算法能够正常运行，并且还需要自己手动添加特征属性，即每个特征的离散型和连续型情况。

最后将构建好的决策树剪枝，然后再打印出来。

因为纸张宽度有限，只能展示部分效果，具体结果请自行在python内检查。

A3：

利用高斯混合模型得到软分类，然后对软分类进行一个ROC检测

具体做法：对数据进行预处理（one-hot）编码后进一步处理完整数据（拼接方法）再将完整数据划分为训练集和测试集，对训练集样本进行高斯混合模型的计算，再对构建好的模型代入测试集判断正误。

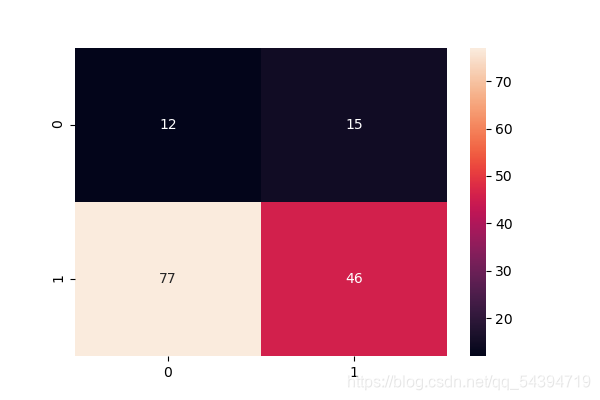
得到如下结果：

Accuracy: 0.3867

precision recall f1-score support

0 0.13 0.44 0.21 27

1 0.75 0.37 0.50 123

accuracy 0.39 150

macro avg 0.44 0.41 0.35 150

weighted avg 0.64 0.39 0.45 150

实验代码

D1：

基于小时的多元线性拟合

import pandas as pd
from statsmodels.formula.api import ols
import random
data_day = pd.read_csv('hour.csv')
data_day = data_day.drop(['instant'], axis=1)
random.seed(123) #设立随机数种子
a = random.sample(range(len(data_day)),round(len(data_day)*0.3))
data_day_test = []
for i in a:
    data_day_test.append(data_day.iloc[i])
data_day_test = pd.DataFrame(data_day_test)
data_day_train = data_day.drop(a)
for i in [data_day_test,data_day_train]:
    i.index = range(i.shape[0])
lm = ols('cnt~temp+atemp+hum+windspeed',data=data_day_train).fit()
print(lm.summary())

基于每日的多元线性拟合


import pandas as pd
from statsmodels.formula.api import ols
import random
data_day = pd.read_csv('day.csv')
data_day = data_day.drop(['instant'], axis=1)
random.seed(123) #设立随机数种子
a = random.sample(range(len(data_day)),round(len(data_day)*0.3))
data_day_test = []
for i in a:
    data_day_test.append(data_day.iloc[i])
data_day_test = pd.DataFrame(data_day_test)
data_day_train = data_day.drop(a)
for i in [data_day_test,data_day_train]:
    i.index = range(i.shape[0])
lm = ols('cnt~temp+atemp+hum+windspeed',data=data_day_train).fit()
print(lm.summary())

D2：

import C45
import treePlotter
import pandas as pd
import numpy as np
# 读取数据文件
data = pd.read_csv('credit.csv',).replace('unknown', 'N')
data = data.fillna(method= 'pad')
# 设定权重
one = np.ones((999,1))
labels = data.columns.values.tolist()
dataSet_test = data[999:].values.tolist()
data = data[0:999].values.tolist()
data = np.array(data)
data = data.reshape((-1, 21))
result = data[:, 20]
result = result.reshape(999,1)
data = data[:, :20]
x = np.c_[data, one]
x = np.c_[x, result]
x = x.tolist()
labelProperties = [0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
classList = [1, 2]
# 构建决策树
trees = C45.createTree(x, labels, labelProperties)
# 利用验证集对决策树剪枝
C45.postPruningTree(trees, classList, x, dataSet_test, labels, labelProperties)
# 绘制决策树
treePlotter.createPlot(trees)

from math import log
import operator
import os

import re
from numpy import inf
import copy


# 计算信息熵
def calcShannonEnt(dataSet, labelIndex):
    # type: (list) -> float
    numEntries = 0  # 样本数(按权重计算）
    labelCounts = {}
    for featVec in dataSet:  # 遍历每个样本
        if featVec[labelIndex] != 'N':
            weight = float(featVec[-2])
            numEntries += weight
            currentLabel = featVec[-1]  # 当前样本的类别
            if currentLabel not in labelCounts.keys():  # 生成类别字典
                labelCounts[currentLabel] = 0
            labelCounts[currentLabel] += weight  # 数据集的倒数第二个值用来标记样本权重
    shannonEnt = 0.0
    for key in labelCounts:  # 计算信息熵
        prob = float(labelCounts[key]) / numEntries
        shannonEnt = shannonEnt - prob * log(prob, 2)
    return shannonEnt


def splitDataSet(dataSet, axis, value, LorR='N'):
    """
    type: (list, int, string or float, string) -> list
    划分数据集
    axis:按第几个特征划分
    value:划分特征的值
    LorR: N 离散属性; L 小于等于value值; R 大于value值
    """
    retDataSet = []
    featVec = []
    if LorR == 'N':  # 离散属性
        for featVec in dataSet:
            if featVec[axis] == value:
                reducedFeatVec = featVec[:axis]
                reducedFeatVec.extend(featVec[axis + 1:])
                retDataSet.append(reducedFeatVec)
    elif LorR == 'L':
        for featVec in dataSet:
            if featVec[axis] != 'N':
                if float(featVec[axis]) < value:
                    retDataSet.append(featVec)
    elif LorR == 'R':
        for featVec in dataSet:
            if featVec[axis] != 'N':
                if float(featVec[axis]) > value:
                    retDataSet.append(featVec)
    return retDataSet


def splitDataSetWithNull(dataSet, axis, value, LorR='N'):
    """
    type: (list, int, string or float, string) -> list
    划分数据集
    axis:按第几个特征划分
    value:划分特征的值
    LorR: N 离散属性; L 小于等于value值; R 大于value值
    """
    retDataSet = []
    nullDataSet = []
    featVec = []
    totalWeightV = calcTotalWeight(dataSet, axis, False)  # 非空样本权重
    totalWeightSub = 0.0
    if LorR == 'N':  # 离散属性
        for featVec in dataSet:
            if featVec[axis] == value:
                reducedFeatVec = featVec[:axis]
                reducedFeatVec.extend(featVec[axis + 1:])
                retDataSet.append(reducedFeatVec)
            elif featVec[axis] == 'N':
                reducedNullVec = featVec[:axis]
                reducedNullVec.extend(featVec[axis + 1:])
                nullDataSet.append(reducedNullVec)
    elif LorR == 'L':
        for featVec in dataSet:
            if featVec[axis] != 'N':
                if float(featVec[axis]) < value:
                    retDataSet.append(featVec)
            elif featVec[axis] == 'N':
                nullDataSet.append(featVec)
    elif LorR == 'R':
        for featVec in dataSet:
            if featVec[axis] != 'N':
                if float(featVec[axis]) > value:
                    retDataSet.append(featVec)
            elif featVec[axis] == 'N':
                nullDataSet.append(featVec)

    totalWeightSub = calcTotalWeight(retDataSet, -1, True)  # 计算此分支中非空样本的总权重
    for nullVec in nullDataSet:  # 把缺失值样本按权值比例划分到分支中
        nullVec[-2] = float(nullVec[-2]) * totalWeightSub / totalWeightV
        retDataSet.append(nullVec)

    return retDataSet


def calcTotalWeight(dataSet, labelIndex, isContainNull):
    """
    type: (list, int, bool) -> float
    计算样本集对某个特征值的总样本树（按权重计算）
    :param dataSet: 数据集
    :param labelIndex: 特征值索引
    :param isContainNull: 是否包含空值的样本
    :return: 返回样本集的总权重值
    """
    totalWeight = 0.0
    for featVec in dataSet:  # 遍历每个样本
        weight = float(featVec[-2])
        if isContainNull is False and featVec[labelIndex] != 'N':
            totalWeight += weight  # 非空样本树，按权重计算
        if isContainNull is True:
            totalWeight += weight  # 总样本数，按权重计算
    return totalWeight


def calcGain(dataSet, labelIndex, labelPropertyi):
    """
    type: (list, int, int) -> float, int
    计算信息增益,返回信息增益值和连续属性的划分点
    dataSet: 数据集
    labelIndex: 特征值索引
    labelPropertyi: 特征值类型，0为离散，1为连续
    """
    baseEntropy = calcShannonEnt(dataSet, labelIndex)  # 计算根节点的信息熵
    featList = [example[labelIndex] for example in dataSet]  # 特征值列表
    uniqueVals = set(featList)  # 该特征包含的所有值
    newEntropy = 0.0
    totalWeight = 0.0
    totalWeightV = 0.0
    totalWeight = calcTotalWeight(dataSet, labelIndex, True)  # 总样本权重
    totalWeightV = calcTotalWeight(dataSet, labelIndex, False)  # 非空样本权重
    if labelPropertyi == 0:  # 对离散的特征
        for value in uniqueVals:  # 对每个特征值，划分数据集, 计算各子集的信息熵
            if value != 'N':
                subDataSet = splitDataSet(dataSet, labelIndex, value)
                totalWeightSub = 0.0
                totalWeightSub = calcTotalWeight(subDataSet, labelIndex, True)
                prob = totalWeightSub / totalWeightV
                newEntropy += prob * calcShannonEnt(subDataSet, labelIndex)
    else:  # 对连续的特征
        uniqueValsList = list(uniqueVals)
        if 'N' in uniqueValsList:
            uniqueValsList.remove('N')
        sortedUniqueVals = sorted(uniqueValsList)  # 对特征值排序
        listPartition = []
        minEntropy = inf
        if len(sortedUniqueVals) == 1:  # 如果只有一个值，可以看作只有左子集，没有右子集
            totalWeightLeft = calcTotalWeight(dataSet, labelIndex, True)
            probLeft = totalWeightLeft / totalWeightV
            minEntropy = probLeft * calcShannonEnt(dataSet, labelIndex)
        else:
            for j in range(len(sortedUniqueVals) - 1):  # 计算划分点
                partValue = (float(sortedUniqueVals[j]) + float(
                    sortedUniqueVals[j + 1])) / 2
                # 对每个划分点，计算信息熵
                dataSetLeft = splitDataSet(dataSet, labelIndex, partValue, 'L')
                dataSetRight = splitDataSet(dataSet, labelIndex, partValue, 'R')
                totalWeightLeft = 0.0
                totalWeightLeft = calcTotalWeight(dataSetLeft, labelIndex, True)
                totalWeightRight = 0.0
                totalWeightRight = calcTotalWeight(dataSetRight, labelIndex, True)
                probLeft = totalWeightLeft / totalWeightV
                probRight = totalWeightRight / totalWeightV
                Entropy = probLeft * calcShannonEnt(dataSetLeft, labelIndex) + \
                          probRight * calcShannonEnt(dataSetRight, labelIndex)
                if Entropy < minEntropy:  # 取最小的信息熵
                    minEntropy = Entropy
        newEntropy = minEntropy
    gain = totalWeightV / totalWeight * (baseEntropy - newEntropy)
    return gain


def calcGainRatio(dataSet, labelIndex, labelPropertyi):
    """
    type: (list, int, int) -> float, int
    计算信息增益率,返回信息增益率和连续属性的划分点
    dataSet: 数据集
    labelIndex: 特征值索引
    labelPropertyi: 特征值类型，0为离散，1为连续
    """
    baseEntropy = calcShannonEnt(dataSet, labelIndex)  # 计算根节点的信息熵
    featList = [example[labelIndex] for example in dataSet]  # 特征值列表
    uniqueVals = set(featList)  # 该特征包含的所有值
    newEntropy = 0.0
    bestPartValuei = None
    IV = 0.0
    totalWeight = 0.0
    totalWeightV = 0.0
    totalWeight = calcTotalWeight(dataSet, labelIndex, True)  # 总样本权重
    totalWeightV = calcTotalWeight(dataSet, labelIndex, False)  # 非空样本权重
    if labelPropertyi == 0:  # 对离散的特征
        for value in uniqueVals:  # 对每个特征值，划分数据集, 计算各子集的信息熵
            subDataSet = splitDataSet(dataSet, labelIndex, value)
            totalWeightSub = 0.0
            totalWeightSub = calcTotalWeight(subDataSet, labelIndex, True)
            if value != 'N':
                prob = totalWeightSub / totalWeightV
                newEntropy += prob * calcShannonEnt(subDataSet, labelIndex)
            prob1 = totalWeightSub / totalWeight
            IV -= prob1 * log(prob1, 2)
    else:  # 对连续的特征
        uniqueValsList = list(uniqueVals)
        if 'N' in uniqueValsList:
            uniqueValsList.remove('N')
            # 计算空值样本的总权重，用于计算IV
            totalWeightN = 0.0
            dataSetNull = splitDataSet(dataSet, labelIndex, 'N')
            totalWeightN = calcTotalWeight(dataSetNull, labelIndex, True)
            probNull = totalWeightN / totalWeight
            if probNull > 0.0:
                IV += -1 * probNull * log(probNull, 2)

        sortedUniqueVals = sorted(uniqueValsList)  # 对特征值排序
        listPartition = []
        minEntropy = inf

        if len(sortedUniqueVals) == 1:  # 如果只有一个值，可以看作只有左子集，没有右子集
            totalWeightLeft = calcTotalWeight(dataSet, labelIndex, True)
            probLeft = totalWeightLeft / totalWeightV
            minEntropy = probLeft * calcShannonEnt(dataSet, labelIndex)
            IV = -1 * probLeft * log(probLeft, 2)
        else:
            for j in range(len(sortedUniqueVals) - 1):  # 计算划分点
                partValue = (float(sortedUniqueVals[j]) + float(
                    sortedUniqueVals[j + 1])) / 2
                # 对每个划分点，计算信息熵
                dataSetLeft = splitDataSet(dataSet, labelIndex, partValue, 'L')
                dataSetRight = splitDataSet(dataSet, labelIndex, partValue, 'R')
                totalWeightLeft = 0.0
                totalWeightLeft = calcTotalWeight(dataSetLeft, labelIndex, True)
                totalWeightRight = 0.0
                totalWeightRight = calcTotalWeight(dataSetRight, labelIndex, True)
                probLeft = totalWeightLeft / totalWeightV
                probRight = totalWeightRight / totalWeightV
                Entropy = probLeft * calcShannonEnt(
                    dataSetLeft, labelIndex) + probRight * calcShannonEnt(dataSetRight, labelIndex)
                if Entropy < minEntropy:  # 取最小的信息熵
                    minEntropy = Entropy
                    bestPartValuei = partValue
                    probLeft1 = totalWeightLeft / totalWeight
                    probRight1 = totalWeightRight / totalWeight
                    IV += -1 * (probLeft1 * log(probLeft1, 2) + probRight1 * log(probRight1, 2))

        newEntropy = minEntropy
    gain = totalWeightV / totalWeight * (baseEntropy - newEntropy)
    if IV == 0.0:  # 如果属性只有一个值，IV为0，为避免除数为0，给个很小的值
        IV = 0.0000000001
    gainRatio = gain / IV
    return gainRatio, bestPartValuei


# 选择最好的数据集划分方式
def chooseBestFeatureToSplit(dataSet, labelProperty):
    """
    type: (list, int) -> int, float
    :param dataSet: 样本集
    :param labelProperty: 特征值类型，1 连续， 0 离散
    :return: 最佳划分属性的索引和连续属性的划分值
    """
    numFeatures = len(labelProperty)  # 特征数
    bestInfoGainRatio = 0.0
    bestFeature = -1
    bestPartValue = None  # 连续的特征值，最佳划分值
    gainSum = 0.0
    gainAvg = 0.0
    for i in range(numFeatures):  # 对每个特征循环
        infoGain = calcGain(dataSet, i, labelProperty[i])
        gainSum += infoGain
    gainAvg = gainSum / numFeatures
    for i in range(numFeatures):  # 对每个特征循环
        infoGainRatio, bestPartValuei = calcGainRatio(dataSet, i, labelProperty[i])
        infoGain = calcGain(dataSet, i, labelProperty[i])
        if infoGainRatio > bestInfoGainRatio and infoGain > gainAvg:  # 取信息增益高于平均增益且信息增益率最大的特征
            bestInfoGainRatio = infoGainRatio
            bestFeature = i
            bestPartValue = bestPartValuei
    return bestFeature, bestPartValue


# 通过排序返回出现次数最多的类别
def majorityCnt(classList, weightList):
    classCount = {}
    for i in range(len(classList)):
        if classList[i] not in classCount.keys():
            classCount[classList[i]] = 0.0
        classCount[classList[i]] += round(float(weightList[i]),1)

    # python 2.7
    # sortedClassCount = sorted(classCount.iteritems(),
    #                         key=operator.itemgetter(1), reverse=True)
    sortedClassCount = sorted(classCount.items(),
                              key=operator.itemgetter(1), reverse=True)
    if len(sortedClassCount) == 1:
        return (sortedClassCount[0][0],sortedClassCount[0][1],0.0)
    return (sortedClassCount[0][0], sortedClassCount[0][1], sortedClassCount[1][1])


# 创建树, 样本集 特征 特征属性（0 离散， 1 连续）
def createTree(dataSet, labels, labelProperty):
    classList = [example[-1] for example in dataSet]  # 类别向量
    weightList = [example[-2] for example in dataSet]  # 权重向量
    if classList.count(classList[0]) == len(classList):  # 如果只有一个类别，返回
        totalWeiht = calcTotalWeight(dataSet,0,True)
        return (classList[0], round(totalWeiht,1),0.0)
    #totalWeight = calcTotalWeight(dataSet, 0, True)
    if len(dataSet[0]) == 1:  # 如果所有特征都被遍历完了，返回出现次数最多的类别
        return majorityCnt(classList)
    bestFeat, bestPartValue = chooseBestFeatureToSplit(dataSet,
                                                       labelProperty)  # 最优分类特征的索引
    if bestFeat == -1:  # 如果无法选出最优分类特征，返回出现次数最多的类别
        return majorityCnt(classList, weightList)
    if labelProperty[bestFeat] == 0:  # 对离散的特征
        bestFeatLabel = labels[bestFeat]
        myTree = {bestFeatLabel: {}}
        labelsNew = copy.copy(labels)
        labelPropertyNew = copy.copy(labelProperty)
        del (labelsNew[bestFeat])  # 已经选择的特征不再参与分类
        del (labelPropertyNew[bestFeat])
        featValues = [example[bestFeat] for example in dataSet]
        uniqueValue = set(featValues)  # 该特征包含的所有值
        uniqueValue.discard('N')
        for value in uniqueValue:  # 对每个特征值，递归构建树
            subLabels = labelsNew[:]
            subLabelProperty = labelPropertyNew[:]
            myTree[bestFeatLabel][value] = createTree(
                splitDataSetWithNull(dataSet, bestFeat, value), subLabels,
                subLabelProperty)
    else:  # 对连续的特征，不删除该特征，分别构建左子树和右子树
        bestFeatLabel = labels[bestFeat] + '<' + str(bestPartValue)
        myTree = {bestFeatLabel: {}}
        subLabels = labels[:]
        subLabelProperty = labelProperty[:]
        # 构建左子树
        valueLeft = 'Y'
        myTree[bestFeatLabel][valueLeft] = createTree(
            splitDataSetWithNull(dataSet, bestFeat, bestPartValue, 'L'), subLabels,
            subLabelProperty)
        # 构建右子树
        valueRight = 'N'
        myTree[bestFeatLabel][valueRight] = createTree(
            splitDataSetWithNull(dataSet, bestFeat, bestPartValue, 'R'), subLabels,
            subLabelProperty)
    return myTree


# 测试算法
def classify(inputTree, classList, featLabels, featLabelProperties, testVec):
    firstStr = list(inputTree.keys())[0]  # 根节点
    firstLabel = firstStr
    lessIndex = str(firstStr).find('<')
    if lessIndex > -1:  # 如果是连续型的特征
        firstLabel = str(firstStr)[:lessIndex]
    secondDict = inputTree[firstStr]
    featIndex = featLabels.index(firstLabel)  # 跟节点对应的特征
    classLabel = {}
    for classI in classList:
        classLabel[classI] = 0.0
    for key in secondDict.keys():  # 对每个分支循环
        if featLabelProperties[featIndex] == 0:  # 离散的特征
            if testVec[featIndex] == key:  # 测试样本进入某个分支
                if type(secondDict[key]).__name__ == 'dict':  # 该分支不是叶子节点，递归
                    classLabelSub = classify(secondDict[key], classList, featLabels,
                                          featLabelProperties, testVec)
                    for classKey in classLabel.keys():
                        classLabel[classKey] += classLabelSub[classKey]
                else:  # 如果是叶子， 返回结果
                    for classKey in classLabel.keys():
                        if classKey == secondDict[key][0]:
                            classLabel[classKey] += secondDict[key][1]
                        else:
                            classLabel[classKey] += secondDict[key][2]
            elif testVec[featIndex] == 'N':  # 如果测试样本的属性值缺失，则进入每个分支
                if type(secondDict[key]).__name__ == 'dict':  # 该分支不是叶子节点，递归
                    classLabelSub = classify(secondDict[key], classList, featLabels,
                                          featLabelProperties, testVec)
                    for classKey in classLabel.keys():
                        classLabel[classKey] += classLabelSub[key]
                else:  # 如果是叶子， 返回结果
                    for classKey in classLabel.keys():
                        if classKey == secondDict[key][0]:
                            classLabel[classKey] += secondDict[key][1]
                        else:
                            classLabel[classKey] += secondDict[key][2]
        else:
            partValue = float(str(firstStr)[lessIndex + 1:])
            if testVec[featIndex] == 'N':  # 如果测试样本的属性值缺失，则对每个分支的结果加和
                # 进入左子树
                if type(secondDict[key]).__name__ == 'dict':  # 该分支不是叶子节点，递归
                    classLabelSub = classify(secondDict[key], classList, featLabels,
                                          featLabelProperties, testVec)
                    for classKey in classLabel.keys():
                        classLabel[classKey] += classLabelSub[classKey]
                else:  # 如果是叶子， 返回结果
                    for classKey in classLabel.keys():
                        if classKey == secondDict[key][0]:
                            classLabel[classKey] += secondDict[key][1]
                        else:
                            classLabel[classKey] += secondDict[key][2]
            elif float(testVec[featIndex]) <= partValue and key == 'Y':  # 进入左子树
                if type(secondDict['Y']).__name__ == 'dict':  # 该分支不是叶子节点，递归
                    classLabelSub = classify(secondDict['Y'], classList, featLabels,
                                             featLabelProperties, testVec)
                    for classKey in classLabel.keys():
                        classLabel[classKey] += classLabelSub[classKey]
                else:  # 如果是叶子， 返回结果
                    for classKey in classLabel.keys():
                        if classKey == secondDict[key][0]:
                            classLabel[classKey] += secondDict['Y'][1]
                        else:
                            classLabel[classKey] += secondDict['Y'][2]
            elif float(testVec[featIndex]) > partValue and key == 'N':
                if type(secondDict['N']).__name__ == 'dict':  # 该分支不是叶子节点，递归
                    classLabelSub = classify(secondDict['N'], classList, featLabels,
                                             featLabelProperties, testVec)
                    for classKey in classLabel.keys():
                        classLabel[classKey] += classLabelSub[classKey]
                else:  # 如果是叶子， 返回结果
                    for classKey in classLabel.keys():
                        if classKey == secondDict[key][0]:
                            classLabel[classKey] += secondDict['N'][1]
                        else:
                            classLabel[classKey] += secondDict['N'][2]

    return classLabel


# 存储决策树
def storeTree(inputTree, filename):
    import pickle
    fw = open(filename, 'w')
    pickle.dump(inputTree, fw)
    fw.close()


# 读取决策树, 文件不存在返回None
def grabTree(filename):
    import pickle
    if os.path.isfile(filename):
        fr = open(filename)
        return pickle.load(fr)
    else:
        return None


# 测试决策树正确率
def testing(myTree, classList, data_test, labels, labelProperties):
    error = 0.0
    for i in range(len(data_test)):
        classLabelSet = classify(myTree, classList, labels, labelProperties, data_test[i])
        maxWeight = 0.0
        classLabel = ''
        for item in classLabelSet.items():
            if item[1] > maxWeight:
                classLabel = item[0]
        if classLabel !=  data_test[i][-1]:
            error += 1
    return float(error)


# 测试投票节点正确率
def testingMajor(major, data_test):
    error = 0.0
    for i in range(len(data_test)):
        if major[0] != data_test[i][-1]:
            error += 1
    # print 'major %d' %error
    return float(error)


# 后剪枝
def postPruningTree(inputTree, classSet, dataSet, data_test, labels, labelProperties):
    firstStr = list(inputTree.keys())[0]
    secondDict = inputTree[firstStr]
    classList = [example[-1] for example in dataSet]
    weightList = [example[-2] for example in dataSet]
    featkey = copy.deepcopy(firstStr)
    if '<' in firstStr:  # 对连续的特征值，使用正则表达式获得特征标签和value
        featkey = re.compile("(.+<)").search(firstStr).group()[:-1]
        featvalue = float(re.compile("(<.+)").search(firstStr).group()[1:])
    labelIndex = labels.index(featkey)
    temp_labels = copy.deepcopy(labels)
    temp_labelProperties = copy.deepcopy(labelProperties)
    if labelProperties[labelIndex] == 0:  # 离散特征
        del (labels[labelIndex])
        del (labelProperties[labelIndex])
    for key in secondDict.keys():  # 对每个分支
        if type(secondDict[key]).__name__ == 'dict':  # 如果不是叶子节点
            if temp_labelProperties[labelIndex] == 0:  # 离散的
                subDataSet = splitDataSet(dataSet, labelIndex, key)
                subDataTest = splitDataSet(data_test, labelIndex, key)
            else:
                if key == 'Y':
                    subDataSet = splitDataSet(dataSet, labelIndex, featvalue,
                                              'L')
                    subDataTest = splitDataSet(data_test, labelIndex,
                                               featvalue, 'L')
                else:
                    subDataSet = splitDataSet(dataSet, labelIndex, featvalue,
                                              'R')
                    subDataTest = splitDataSet(data_test, labelIndex,
                                               featvalue, 'R')
            if len(subDataTest) > 0:
                inputTree[firstStr][key] = postPruningTree(secondDict[key], classSet,
                                                       subDataSet, subDataTest,
                                                       copy.deepcopy(labels),
                                                       copy.deepcopy(
                                                           labelProperties))
    if testing(inputTree, classSet, data_test, temp_labels,
               temp_labelProperties) <= testingMajor(majorityCnt(classList, weightList),
                                                     data_test):
        return inputTree
    return majorityCnt(classList,weightList)

import matplotlib.pyplot as plt

decisionNode = dict(boxstyle="sawtooth", fc="0.8")
leafNode = dict(boxstyle="round4", fc="0.8")
arrow_args = dict(arrowstyle="<-")


def plotNode(nodeTxt, centerPt, parentPt, nodeType):
    createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction', \
                            xytext=centerPt, textcoords='axes fraction', \
                            va="center", ha="center", bbox=nodeType, arrowprops=arrow_args)


def getNumLeafs(myTree):
    numLeafs = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':
            numLeafs += getNumLeafs(secondDict[key])
        else:
            numLeafs += 1
    return numLeafs


def getTreeDepth(myTree):
    maxDepth = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':
            thisDepth = getTreeDepth(secondDict[key]) + 1
        else:
            thisDepth = 1
        if thisDepth > maxDepth:
            maxDepth = thisDepth
    return maxDepth


def plotMidText(cntrPt, parentPt, txtString):
    xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0]
    yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1]
    createPlot.ax1.text(xMid, yMid, txtString)


def plotTree(myTree, parentPt, nodeTxt):
    numLeafs = getNumLeafs(myTree)
    depth = getTreeDepth(myTree)
    firstStr = list(myTree.keys())[0]
    cntrPt = (plotTree.xOff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalw, plotTree.yOff)
    plotMidText(cntrPt, parentPt, nodeTxt)
    plotNode(firstStr, cntrPt, parentPt, decisionNode)
    secondDict = myTree[firstStr]
    plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':
            plotTree(secondDict[key], cntrPt, str(key))
        else:
            plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalw
            plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
            plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
    plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD


def createPlot(inTree):
    fig = plt.figure(1, facecolor='white')
    fig.clf()
    axprops = dict(xticks=[], yticks=[])
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)
    plotTree.totalw = float(getNumLeafs(inTree))
    plotTree.totalD = float(getTreeDepth(inTree))
    plotTree.xOff = -0.5 / plotTree.totalw
    plotTree.yOff = 1.0
    plotTree(inTree, (0.5, 1.0), '')
    plt.show()

D3：

import numpy as np
import pandas as pd


import seaborn as sns
import matplotlib.pyplot as plt
import sklearn.metrics as metrics
from sklearn.mixture import GaussianMixture
from sklearn.model_selection import train_test_split

data = pd.read_csv('dress-recommendation.csv')
# 确定字符型标签
dummpy_list = ['Style', 'Price', 'Size', 'Season', 'NeckLine', 'SleeveLength', 'waiseline','Material',
               'FabricType','Decoration','Pattern Type']
# 将所有字符型数据进行one-hot编码处理
transfer_list = [pd.get_dummies(data[[feature]], prefix = feature+'_') for feature in dummpy_list]
transfer_list.append(data[['Rating','Recommendation']])
# 拼接数据
new_data = pd.concat(transfer_list, axis = 1)


def evaluate(pred, test_y):

    # 输出分类的准确率
    print("Accuracy: %.4f" % (metrics.accuracy_score(test_y, pred)))

    # 输出衡量分类效果的各项指标
    print(metrics.classification_report(test_y, pred))

    # 更直观的，我们通过seaborn画出混淆矩阵
    plt.figure(figsize=(6, 4))
    colorMetrics = metrics.confusion_matrix(test_y, pred)

    # 坐标y代表test_y，即真实的类别，坐标x代表估计出的类别pred
    sns.heatmap(colorMetrics, annot=True, fmt='d', xticklabels=[0, 1], yticklabels=[0, 1])
    plt.show()

X_train, X_test, y_train, y_test = train_test_split(new_data.iloc[:,:-1], new_data['Recommendation'], test_size = .3, random_state = 0)

cov_type = ['full', 'tied', 'diag', 'spherical']

model_list = [GaussianMixture(n_components = 2, covariance_type = cov_name, init_params='random', max_iter=20) for cov_name in cov_type]
# 标签去重
reco_label = np.unique(y_train)
#取纵轴上的平均值
mean_list = np.array([X_train[y_train == value].mean(axis = 0) for value in reco_label])
for gmm_model in model_list:
    gmm_model.means_ = mean_list
    gmm_model.fit(X_train)

    y_pred = gmm_model.predict(X_test)
    evaluate(y_test, y_pred)