动手学循环神经网络(RNN | LSTM | GRU)(LSTM预测股票行情 | Pytorch实现完整代码)

本文链接：https://blog.youkuaiyun.com/qq_53769632/article/details/146975578

前言

这期我们讲进入RNN循环神经网络的学习中来，由于卷积神经网络具有平移不变性，使其对于输入有先后顺序的数据(序列数据)处理起来会缺失信息，而RNN神经网络结构就是为解决这一问题而诞生的。

前期回归

动手学卷积神经网络(CNN)( CIFAR-10多分类实战完整代码 | 手把手教你 | Pytorch实现)
动手学卷积神经网络(CNN)(VGG网络模型实现CIFAR-10多分类)(包含 VGG11，VGG13，VGG16，VGG19 | Pytorch 代码实现）

基础知识

循环神经网络

循环神经网络是一类具有短期记忆能力的神经网络，不仅可以接受其他神经元的信息，还可以接受自身的信息，形成具有环路的网络结构。它的参数学习可以通过随时间反向传播算法进行学习。但当输入序列比较长的时候，会存在梯度爆炸和消失问题，称为长期依赖问题。为了解决这一个问题，引入了门控机制，形成了LSTM和GRU。
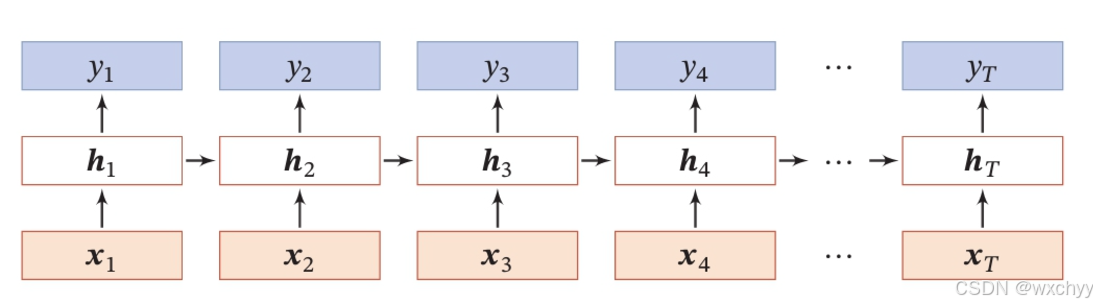
我们先看一下循环神经网络的结构：
在这里插入图片描述
在这其中，U是输入到隐藏层的权重矩阵，W是状态到隐藏层的权值矩阵，s为状态，V是隐藏层到输出层的权值矩阵。
我们将这个隐藏层进行详细展开：

假设x为n维向量，U的大小为n * m 维，W为m * m维，V大小为m * r维， $a_{t-1}$ 为m维向量计算公式：
$a_{t} = f(Ux_{t}+Wa_{t-1})$
$O_{t}=softmax(Va_{t})$
最后输出 $O_{t}$ 是一个r维概率向量，一般表示r个类别的预测概率。
我们最后看一下将其按时间进行展开的结构：
注意：这里不是真实的网络结构，而是这个网络在每个时间t有相同的网络结构，我们将其展开得来的。
在这里插入图片描述

BPTT（时间反向传播算法）

时间反向传播算法其基本原理和反向传播算法是一样的，只不过，反向传播算法是按照层进行反向传播，而BPTT是按照时间t进行反向传播。
在这里插入图片描述
这里就不给出BPTT的反向推导过程了，我们直接看公式：
输出层权重V的梯度：
$L_{t}$ t时刻下的损失。 $L$ 为总损失。

其中交叉熵损失对 softmax 输出的导数：

隐藏层梯度计算：

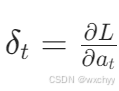
其中 $\text{diag}(\sigma'(a_t))$ 是一个对角矩阵，其对角线上的元素是激活函数 $\sigma$ 在 $a_t$ 处的导数。

输入层到隐藏层权重 U 的梯度：
在这里插入图片描述
隐藏层到隐藏层权重 W 的梯度

最后梯度下降法更新参数：

其中 $\eta$ 是学习率
在这其中我们可以看到W是一个在时间步长中反复被用于相乘的矩阵，我们对矩阵进行特征值分解。

若 $\lambda_i$ 量级上大于1则会爆炸,小于1则会消失，LSTM的出现有效解决了这一问题。

LSTM(长短时记忆网络)

与传统RNN相比，它引入了门结构，LSTM用两个门来控制单元状态c的内容，一个遗忘门，绝对上一时刻的单元状态 $c_{t-1}$ 多少保留，一个是输入门，决定了当前时刻网络的输入有多少保持在单元状态 $c_{t}$ 。同时用输出门来控制单元状态有多少输出到输出值 $h_{t}$ 。通过将隐藏层BPTT更新时求解的连乘，改成了相加的方式进行更新，打破了梯度连乘衰减机制，缓解梯度问题。
在这里插入图片描述
注意：其中z，也称为候选状态 $\tilde{c}_t$ ，输入门控制其有多少信息需要保留。
计算公式如下：

详细计算过程：
1）首先利用上一时刻的外部状态 $h_{t-1}$ 和当前输入的 $x_{t}$ 来计算出三个门，以及候选状态 $\tilde{c}_t$
2）结合遗忘门 $f_{t}$ 和输入门 $i_{t}$ 来更新记忆单元
3）结合输出门 $o_{t}$ 将内部状态信息传递给外部状态 $h_t$
写出矩阵形式如下：
在这里插入图片描述
注意：长短期记忆是指长的“短期记忆”，LSTM网络中，记忆单元c可以在某个时刻捕捉到某个关键信息，并能够将其保持一段时间间隔。

GRU

由于LSTM结构复杂，GRU对LSTM做了简化，相较于LSTM少了一个门，计算效率更高，占用的内存更少。我们发现输入门和遗忘门是互补关系，具有一定的冗余性，将其改为一个更新门，同时将单元状态和输出合并为一个状态。
1）将输入门、遗忘门、输出门变成两个门：更新门 $z_{t}$ 和重置门 $r_{t}$ 。更新门用于控制当前状态需要从历史状态保留多少信息以及从候选状态中接受多少新信息。重置门用于控制候选状态 $\tilde h_{t}$ 是否依赖上一时刻的状态 $h_{t-1}$ 。
2）将单元状态和输出合并为一个状态: $h_{t}$
GRU网络的状态更新方式为：
在这里插入图片描述

GRU网络的循环单元结构如下：

pytorch实现RNN、LSTM以及GRU

torch.nn.RNN(input_size, hidden_size, num_layers=1, nonlinearity='tanh', bias=True, batch_first=False, dropout=0, bidirectional=False)
torch.nn.LSTM(input_size, hidden_size, num_layers=1, bias=True, batch_first=False, dropout=0, bidirectional=False)
torch.nn.GRU(input_size, hidden_size, num_layers=1, bias=True, batch_first=False, dropout=0, bidirectional=False)

input_size：输入x的特征数量。
hidden_size：隐含层的特征数量。
num_layers：RNN的层数。
nonlinearity：指定非线性函数使用tanh还是relu。默认是tanh。
bias：如果是False，那么RNN层就不会使用偏置权重bi和bh，默认是True。
batch_first：如果True的话，那么输入Tensor的shape应该是(batch,seq,feature)，输出也是这样。默认网络输入是(seq,batch,feature)，即序列长度、批次大小、特征维度。
dropout：如果值非零（该参数取值范围为0～1之间），那么除了最后一层外，其他层的输出都会加上一个dropout层，缺省为零。
bidirectional：如果True，将会变成一个双向RNN，默认为False。
注意：
LSTM的参数个数是RNN的4倍，因为LSTM比标准的RNN多了3个线性变换，多出的3个线性变换的权重合在一起是RNN的4倍。
LSTM隐含状态除h0外，多了一个c0，LSTM的输入隐含状态为(h0,c0)，输出的隐含状态为(hn,cn)。

LSTM预测股票行情

数据集

本次数据集来自Baostock，可以直接调Baostock接口，我们可以从中获得我们想要得数据，这里采用沪深300指数数据，时间跨度为2010年1月1日到2023年12年31日。我们这里选择每天最高价格high作为预测目标。数据集为.csv文件。
在这里插入图片描述
这里给出笔者的数据集：
数据集
如果想要自己获得数据集的话可以自行抓取。
1 导入需要的头文件

import pandas as pd # 处理CSV文件
import numpy as np
import torch
import torch.nn as nn
from torch.utils.data import Dataset, DataLoader
from tqdm import tqdm # 进度条
import matplotlib.pyplot as plt # 画损失函数
import datetime # 转化为datatime类型

2 生成训练数据

#通过一个序列来生成一个31*(count(*)-train_end)矩阵（用于处理时序的数据）
#其中最后一列维标签数据。就是把当天的前n天作为参数，当天的数据作为label
def generate_data_by_n_days(series, n, index=False):
    if len(series) <= n:
        raise Exception("The Length of series is %d, while affect by (n=%d)." % (len(series), n))
    df = pd.DataFrame()
    for i in range(n): # 生成类似 c0 c1 ... c29 这样的列，n个特征 最后一列为目标值
        df['c%d' % i] = series.tolist()[i:-(n - i)]
    df['y'] = series.tolist()[n:]

    if index: # index=true返回目标索引
        df.index = series.index[n:]
    return df

# 定义读取数据的函数
def readData(column='high', n=30, all_too=True, index=False, train_end=-500):
    df = pd.read_csv("./data/sh300.csv", index_col=0) # 第一列为日期
    df.index = list(map(lambda x: datetime.datetime.strptime(x, "%Y-%m-%d"), df.index))#索引标准化日期格式并转化为列表类型
    df_column = df[column].copy()
    df_column_train, df_column_test = df_column[:train_end], df_column[train_end - n:] # 划分训练集和测试集
    df_generate_train = generate_data_by_n_days(df_column_train, n, index=index)# 得到训练集
    if all_too: # 返回训练集 全部数据 索引
        return df_generate_train, df_column, df.index.tolist()
    return df_generate_train

将df打印出来，我们可以看到前30列为特征，最后一列为预测值。
在这里插入图片描述

3 规范化数据

#对数据进行预处理，规范化及转换为Tensor
df_numpy = np.array(df)

df_numpy_mean = np.mean(df_numpy)
df_numpy_std = np.std(df_numpy)

df_numpy = (df_numpy - df_numpy_mean) / df_numpy_std
df_tensor = torch.Tensor(df_numpy)

trainset = mytrainset(df_tensor) #自定义数据集
trainloader = DataLoader(trainset, batch_size=batch_size, shuffle=False) # 获取迭代器

4 定义模型

class RNN(nn.Module):
    def __init__(self, input_size):
        super(RNN, self).__init__()
        self.rnn = nn.LSTM( # 定义LSTM
            input_size=input_size,
            hidden_size=64,
            num_layers=1,
            batch_first=True
        )
        self.out = nn.Sequential(
            nn.Linear(64, 1)
        )
    def forward(self, x):
        r_out, (h_n, h_c) = self.rnn(x, None)  #None即隐层状态用0初始化
        out = self.out(r_out)
        return out

网络结构很简单：一个LSTM加一个全连接层输出预测值。
在这里插入图片描述
5 数据读取、预处理、创建数据集及模型初始化

# 参数设置
n = 30
LR = 0.001
EPOCH = 10
batch_size = 32
train_end = -500
# 读取数据
df, df_all, df_index = readData('high', n=n, train_end=train_end)
# 数据预处理
df_numpy = np.array(df)
df_numpy_mean = np.mean(df_numpy)
df_numpy_std = np.std(df_numpy)
df_numpy = (df_numpy - df_numpy_mean) / df_numpy_std
df_tensor = torch.Tensor(df_numpy)
# 创建数据集和数据加载器
trainset = mytrainset(df_tensor)
trainloader = DataLoader(trainset, batch_size=batch_size, shuffle=False)
# 设备选择
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# 初始化模型、优化器和损失函数
rnn = RNN(n).to(device)
optimizer = torch.optim.Adam(rnn.parameters(), lr=LR)
loss_func = nn.MSELoss()

6 训练网络

# 训练模型
total_losses = []
for step in tqdm(range(EPOCH), desc="Training Epochs"):
    epoch_loss = 0
    for tx, ty in trainloader:
        tx = tx.to(device)
        ty = ty.to(device)
        output = rnn(torch.unsqueeze(tx, dim=1)).to(device)
        loss = loss_func(torch.squeeze(output), ty)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        epoch_loss += loss.item()
    avg_loss = epoch_loss / len(trainloader)
    total_losses.append(avg_loss)
    print(f'Epoch {step + 1}/{EPOCH}, Loss: {avg_loss:.4f}')
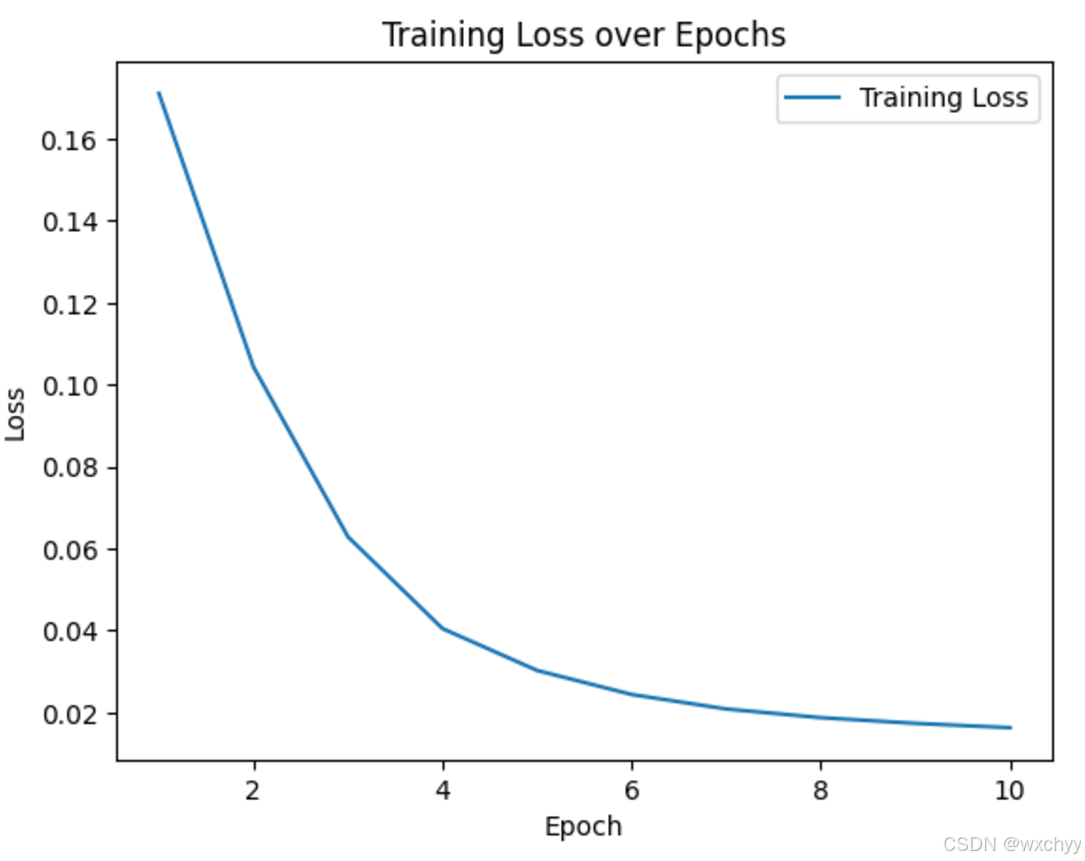
# 绘制损失函数图
plt.plot(range(1, EPOCH + 1), total_losses, label='Training Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Training Loss over Epochs')
plt.legend()
plt.show()

训练过程阶段：

由于数据非常小，10几秒就训练完成了。
在这里插入图片描述
训练结束阶段：

7 测试网络

# 数据标准化
df_all_normal = (df_all - df_numpy_mean) / df_numpy_std
# 将 df_all_normal 转换为 numpy 数组
df_all_normal_numpy = df_all_normal.values
df_all_normal_tensor = torch.Tensor(df_all_normal_numpy).to(device)
# 预测数据
generate_data_train = []
generate_data_test = []
test_index = len(df_all) + train_end
for i in range(n, len(df_all)):
    x = df_all_normal_tensor[i - n:i].to(device)
    x = torch.unsqueeze(torch.unsqueeze(x, dim=0), dim=0)
    y = rnn(x).to(device)
    if i < test_index:
        generate_data_train.append(torch.squeeze(y).detach().cpu().numpy() * df_numpy_std + df_numpy_mean)
    else:
        generate_data_test.append(torch.squeeze(y).detach().cpu().numpy() * df_numpy_std + df_numpy_mean)
# 提取测试集的真实值
test_true = df_all[test_index:].values
# 转换为 numpy 数组
generate_data_test = np.array(generate_data_test)
# 设定误差阈值，这里假设为 10%
error_threshold = 0.10
# 计算误差百分比
error_percentage = np.abs((test_true - generate_data_test) / test_true)
# 统计误差在阈值范围内的样本数量
correct_count = np.sum(error_percentage <= error_threshold)
# 计算“准确率”
accuracy = correct_count / len(test_true)
# 输出“准确率”
print(f"测试集的 '准确率'（误差阈值 {error_threshold * 100}%）: {accuracy * 100}%")


# 可视化
plt.plot(df_index[test_index:], df_all[test_index:], label='real-data')
plt.plot(df_index[test_index:], generate_data_test, label='generate_test')
plt.legend()
plt.show()

在这里插入图片描述

附录

1 RNN实现
其中一种实现。

import torch.nn as nn

class RNN(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(RNN, self).__init__()
        self.hidden_size = hidden_size
        self.i2h = nn.Linear(input_size + hidden_size, hidden_size)
        self.i2o = nn.Linear(input_size + hidden_size, output_size)
        self.softmax = nn.LogSoftmax(dim=1)
    def forward(self, input, hidden):
        combined = torch.cat((input, hidden), 1)
        hidden = self.i2h(combined)
        output = self.i2o(combined)
        output = self.softmax(output)
        return output, hidden

    def initHidden(self):
        return torch.zeros(1, self.hidden_size)

n_hidden = 128
rnn = RNN(n_letters, n_hidden, n_categories)

2 LSTM实现

import torch.nn as nn
import torch

class LSTMCell(nn.Module):
    def __init__(self, input_size, hidden_size, cell_size, output_size):
        super(LSTMCell, self).__init__()
        self.hidden_size = hidden_size
        self.cell_size = cell_size
        self.gate = nn.Linear(input_size + hidden_size, cell_size)
        self.output = nn.Linear(hidden_size, output_size)
        self.sigmoid = nn.Sigmoid()
        self.tanh = nn.Tanh()
        self.softmax = nn.LogSoftmax(dim=1)

    def forward(self, input, hidden, cell):
        combined = torch.cat((input, hidden), 1)
        f_gate = self.sigmoid(self.gate(combined))
        i_gate = self.sigmoid(self.gate(combined))
        o_gate = self.sigmoid(self.gate(combined))
        z_state = self.tanh(self.gate(combined))
        cell = torch.add(torch.mul(cell, f_gate), torch.mul(z_state, i_gate))
        hidden = torch.mul(self.tanh(cell), o_gate)
        output = self.output(hidden)
        output = self.softmax(output)
        return output, hidden, cell

    def initHidden(self):
        return torch.zeros(1, self.hidden_size)

    def initCell(self):
        return torch.zeros(1, self.cell_size)

3 GRU实现

class GRUCell(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(GRUCell, self).__init__()
        self.hidden_size = hidden_size
        self.gate = nn.Linear(input_size + hidden_size, hidden_size)
        self.output = nn.Linear(hidden_size, output_size)
        self.sigmoid = nn.Sigmoid()
        self.tanh = nn.Tanh()
        self.softmax = nn.LogSoftmax(dim=1)

    def forward(self, input, hidden):
        combined = torch.cat((input, hidden), 1)        
        z_gate = self.sigmoid(self.gate(combined))
        r_gate = self.sigmoid(self.gate(combined))
        combined01 = torch.cat((input, torch.mul(hidden,r_gate)), 1)  
        h1_state = self.tanh(self.gate(combined01))

        h_state = torch.add(torch.mul((1-z_gate), hidden), torch.mul(h1_state, z_gate))
        output = self.output(h_state)
        output = self.softmax(output)
        return output, h_state

    def initHidden(self):
        return torch.zeros(1, self.hidden_size)