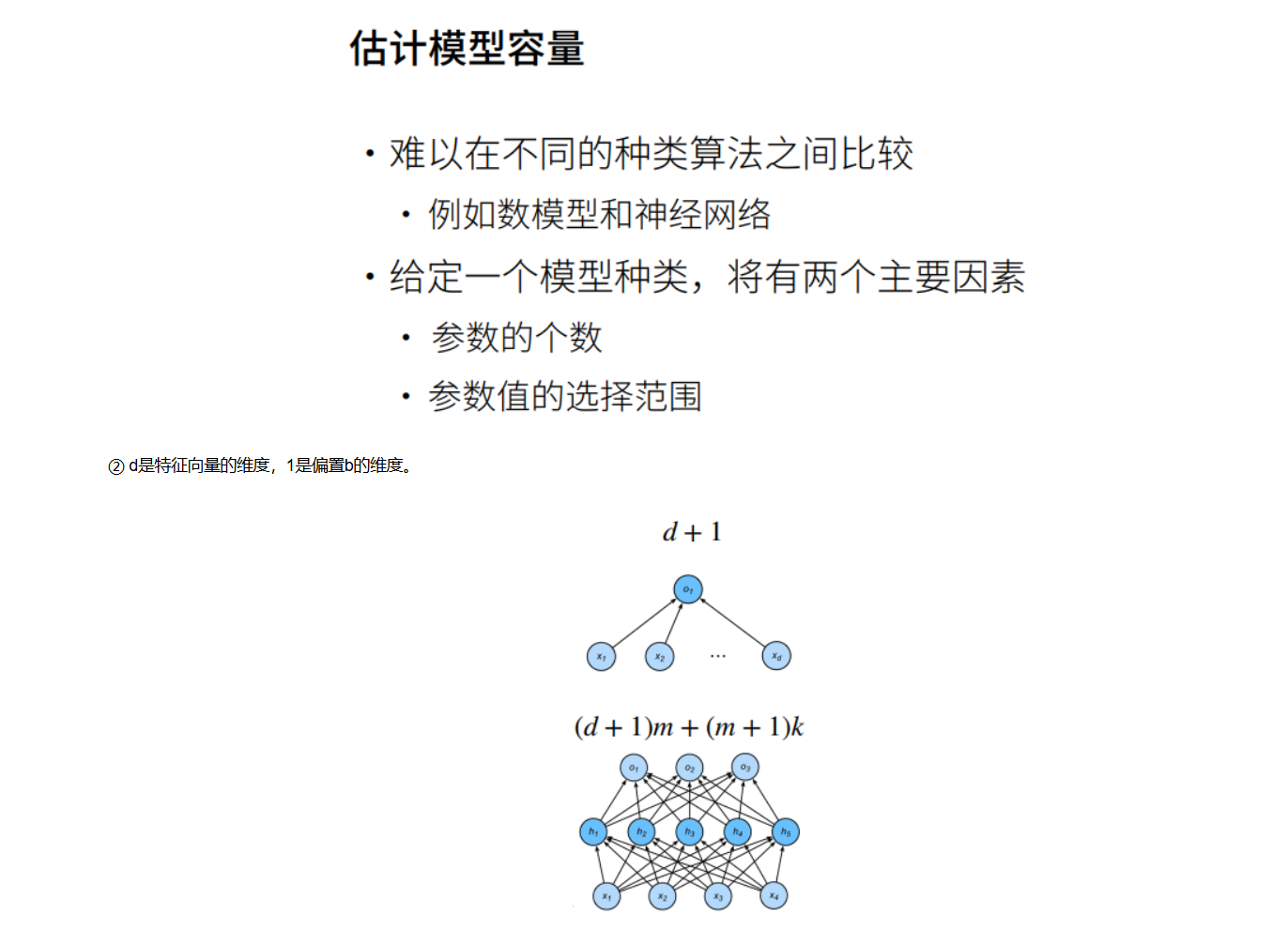
文章目录
摘要
本周主要学习了深度学习的Softmax回归问题、图像分类数据集的代码实现、多层感知机、卷积层学了一部分,统计学习的三要素模型、策略、算法,模型的评估和选择、过拟合、感知机。
This week, I mainly studied Softmax regression problem of deep learning, code implementation of image classification data set, multi-layer perceptron, convolution layer, three-element model of statistical learning, strategy, algorithm, model evaluation and selection, overfitting, perceptron.
Softmax回归问题
Softmax回归虽然它的名字是回归,其实它是一个分类问题。
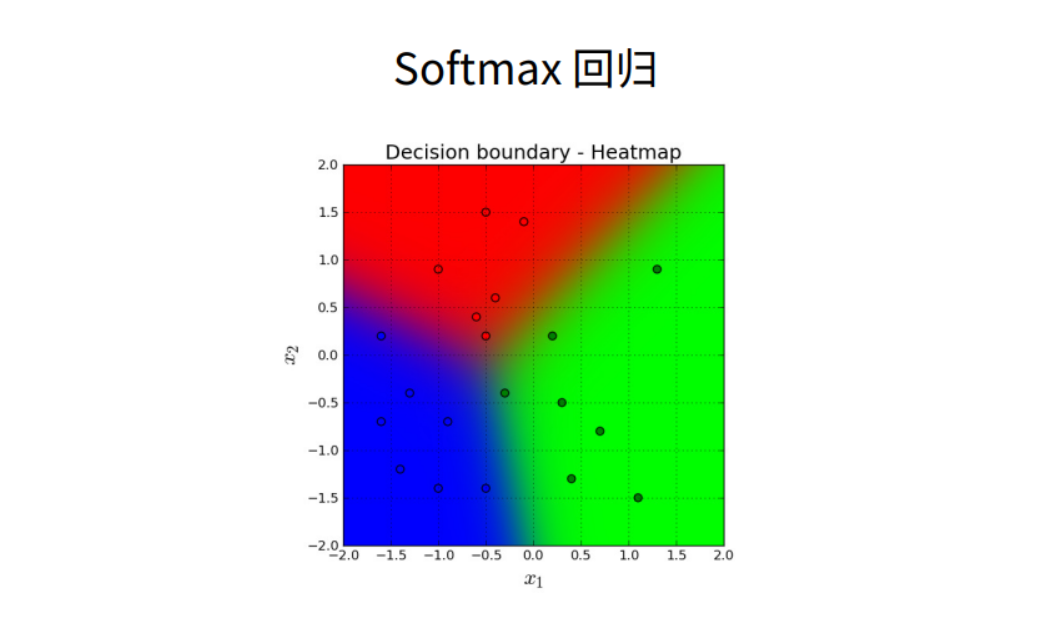
回归VS分类

回归到分类
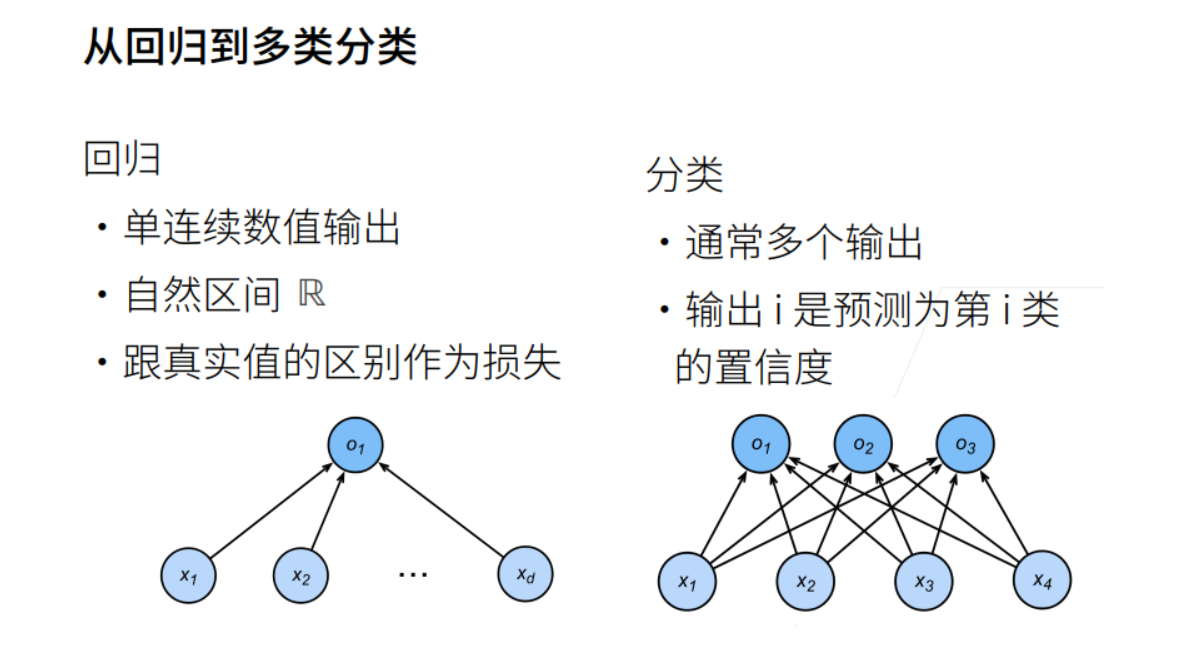
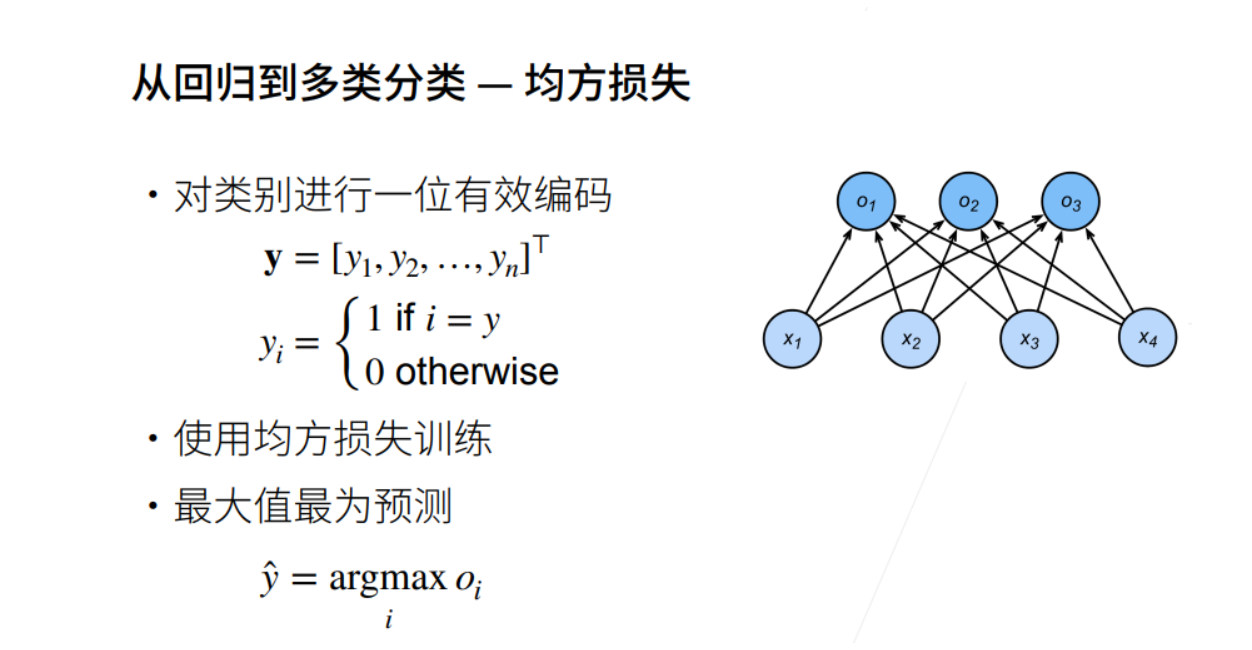
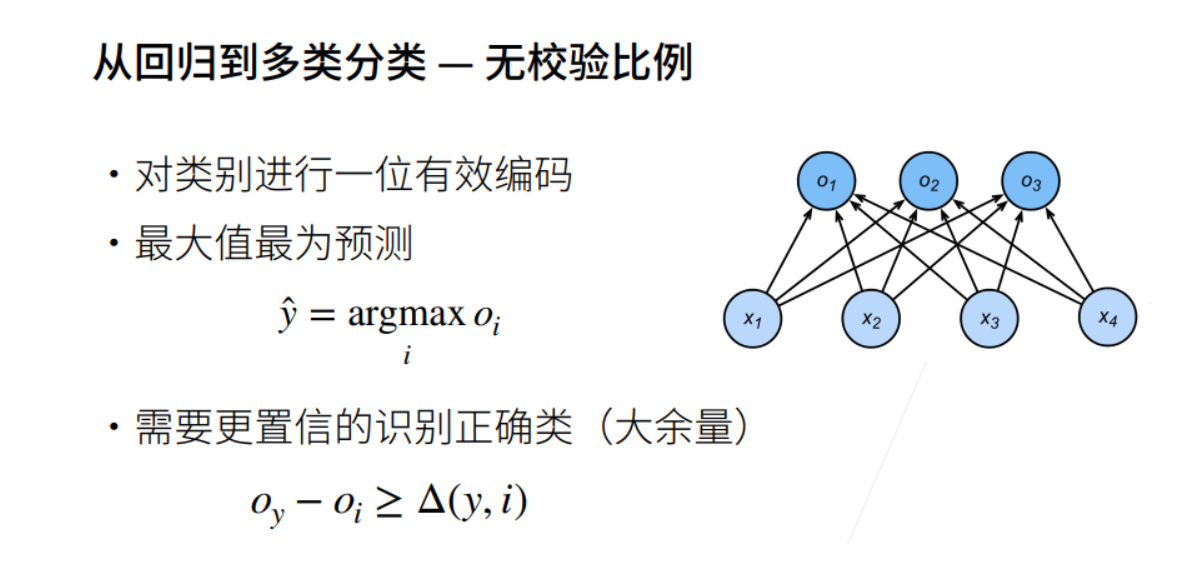
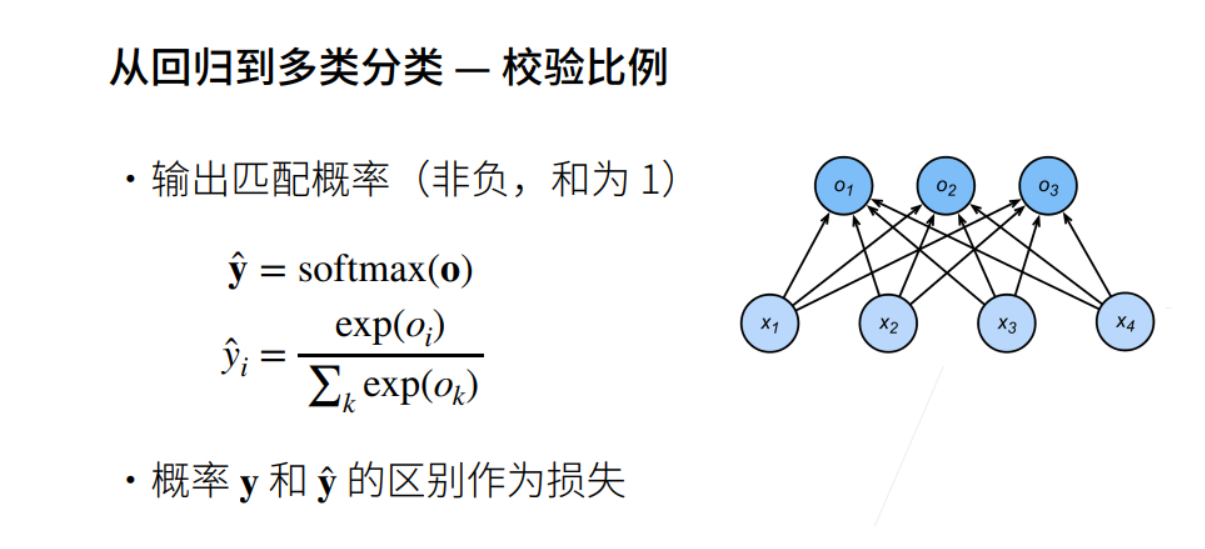
交叉熵损失


损失函数
① 三个常用的损失函数 L2 loss、L1 loss、Huber’s Robust loss。
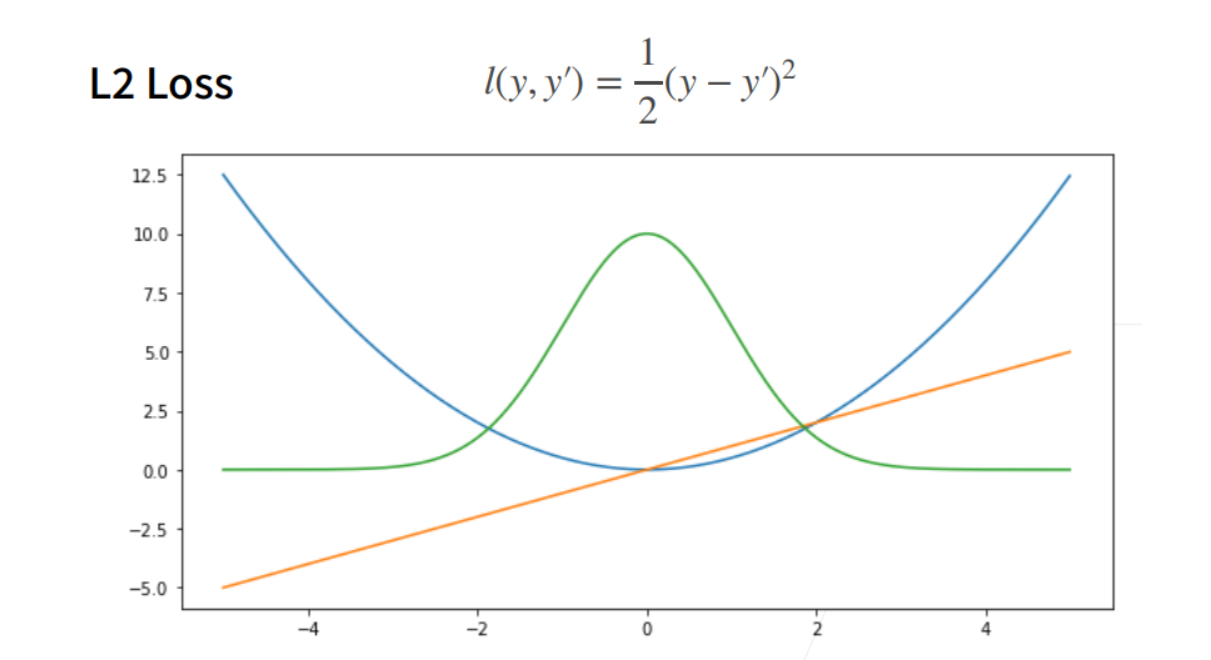
L2 loss
① 蓝色曲线为当y=0时,变换y’所获得的曲线。
② 绿色曲线为当y=0时,变换y’所获得的曲线的似然函数,即 1−𝑙(𝑦,𝑦′)
,似然函数呈高斯分布。最小化损失函数就是最大化似然函数。
③ 橙色曲线为损失函数的梯度,梯度是一次函数,所以穿过原点。
④ 当预测值y’跟真实值y隔的比较远的时候,(真实值y为0,预测值就是下面的曲线里的x轴),梯度比较大,所以参数更新比较多。
⑤ 随着预测值靠近真实值是,梯度越来越小,参数的更新越来越小。
L1 loss
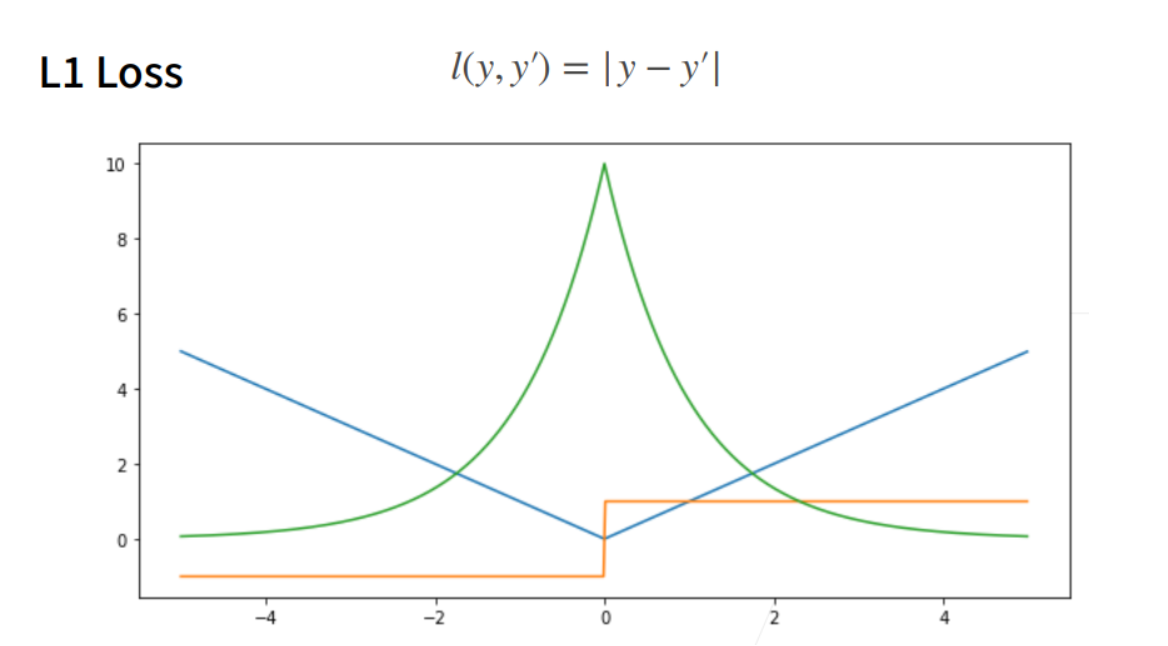
① 相对L2 loss,L1 loss的梯度就是距离原点时,梯度也不是特别大,权重的更新也不是特别大。会带来很多稳定性的好处。
② 他的缺点是在零点处不可导,并在零点处左右有±1的变化,这个不平滑性导致预测值与真实值靠的比较近的时候,优化到末期的时候,可能会不那么稳定。
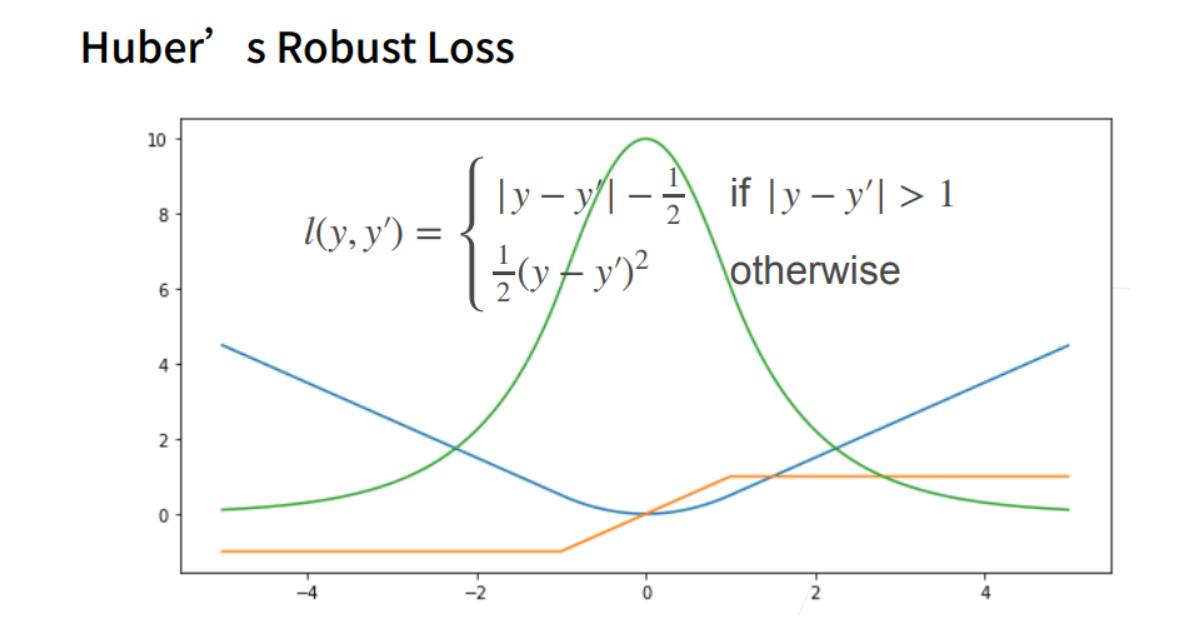
Huber’s Robust loss
① 结合L1 loss 和L2 loss损失。
图像分类数据集
① MINIST数据集是图像分类中广泛使用的数据集之一,但作为基准数据集过于简单。
② 下面将使用类似但更复杂的Fashion-MNIST数据集。
显示图片
%matplotlib inline
import torch
import torchvision
from torch.utils import data
from torchvision import transforms
from d2l import torch as d2l
# SVG是一种无损格式 – 意味着它在压缩时不会丢失任何数据,可以呈现无限数量的颜色。
# SVG最常用于网络上的图形、徽标可供其他高分辨率屏幕上查看。
d2l.use_svg_display() # 使用svg来显示图片,这样清晰度高一些。
数据集下载
%matplotlib inline
import torch
import torchvision
from torch.utils import data
from torchvision import transforms
from d2l import torch as d2l
d2l.use_svg_display()
# 通过ToTensor实例将图像数据从PIL类型变换成32位浮点数格式
# 并除以255使得所有像素的数值均在0到1之间
trans = transforms.ToTensor()
mnist_train = torchvision.datasets.FashionMNIST(root="01_data/01_DataSet_FashionMNIST",train=True,transform=trans,download=True)
mnist_test = torchvision.datasets.FashionMNIST(root="01_data/01_DataSet_FashionMNIST",train=False,transform=trans,download=True)
print(len(mnist_train)) # 训练数据集长度
print(len(mnist_test)) # 测试数据集长度
print(mnist_train[0][0].shape) # 黑白图片,所以channel为1。
print(mnist_train[0][1]) # [0][0]表示第一个样本的图片信息,[0][1]表示该样本对应的标签值
60000
10000
torch.Size([1, 28, 28])
9
可视化数据集
%matplotlib inline
import torch
import torchvision
from torch.utils import data
from torchvision import transforms
from d2l import torch as d2l
d2l.use_svg_display()
# 通过ToTensor实例将图像数据从PIL类型变换成32位浮点数格式
# 并除以255使得所有像素的数值均在0到1之间
trans = transforms.ToTensor()
mnist_train = torchvision.datasets.FashionMNIST(root="01_data/01_DataSet_FashionMNIST",train=True,transform=trans,download=True)
mnist_test = torchvision.datasets.FashionMNIST(root="01_data/01_DataSet_FashionMNIST",train=False,transform=trans,download=True)
def get_fashion_mnist_labels(labels):
"""返回Fashion-MNIST数据集的文本标签"""
text_labels = ['t-shirt','trouser','pullover','dress','coat',
'sandal','shirt','sneaker','bag','ankle boot']
return [text_labels[int(i)] for i in labels]
def show_images(imgs, num_rows, num_cols, titles=None, scale=1.5):
"""Plot a list of images."""
figsize = (num_cols * scale, num_rows * scale) # 传进来的图像尺寸,scale 为放缩比例因子
_, axes = d2l.plt.subplots(num_rows,num_cols,figsize=figsize)
print(_)
print(axes) # axes 为构建的两行九列的画布
axes = axes.flatten()
print(axes) # axes 变成一维数据
for i,(ax,img) in enumerate(zip(axes,imgs)):
if(i<1):
print("i:",i)
print("ax,img:",ax,img)
if torch.is_tensor(img):
# 图片张量
ax.imshow(img.numpy())
ax.set_title(titles[i])
else:
# PIL图片
ax.imshow(img)
X, y = next(iter(data.DataLoader(mnist_train,batch_size=18))) # X,y 为仅抽取一次的18个样本的图片、以及对应的标签值
show_images(X.reshape(18,28,28),2,9,titles=get_fashion_mnist_labels(y))
小批量数据集
%matplotlib inline
import torch
import torchvision
from torch.utils import data
from torchvision import transforms
from d2l import torch as d2l
d2l.use_svg_display()
# 通过ToTensor实例将图像数据从PIL类型变换成32位浮点数格式
# 并除以255使得所有像素的数值均在0到1之间
trans = transforms.ToTensor()
mnist_train = torchvision.datasets.FashionMNIST(root="01_data/01_DataSet_FashionMNIST",train=True,transform=trans,download=True)
mnist_test = torchvision.datasets.FashionMNIST(root="01_data/01_DataSet_FashionMNIST",train=False,transform=trans,download=True)
def get_fashion_mnist_labels(labels):
"""返回Fashion-MNIST数据集的文本标签"""
text_labels = ['t-shirt','trouser','pullover','dress','coat',
'sandal','shirt','sneaker','bag','ankle boot']
return [text_labels[int(i)] for i in labels]
def show_images(imgs, num_rows, num_cols, titles=None, scale=1.5):
"""Plot a list of images."""
figsize = (num_cols * scale, num_rows * scale) # 传进来的图像尺寸,scale 为放缩比例因子
_, axes = d2l.plt.subplots(num_rows,num_cols,figsize=figsize)
print(_)
print(axes) # axes 为构建的两行九列的画布
axes = axes.flatten()
print(axes) # axes 变成一维数据
for i,(ax,img) in enumerate(zip(axes,imgs)):
if torch.is_tensor(img):
# 图片张量
ax.imshow(img.numpy())
ax.set_title(titles[i])
else:
# PIL图片
ax.imshow(img)
X, y = next(iter(data.DataLoader(mnist_train,batch_size=18))) # X,y 为仅抽取一次的18个样本的图片、以及对应的标签值
show_images(X.reshape(18,28,28),2,9,titles=get_fashion_mnist_labels(y))
batch_size = 256
def get_dataloader_workers():
"""使用4个进程来读取的数据"""
return 4
train_iter = data.DataLoader(mnist_train, batch_size, shuffle=True,
num_workers=get_dataloader_workers())
timer = d2l.Timer() # 计时器对象实例化,开始计时
for X,y in train_iter: # 遍历一个batch_size数据的时间
continue
f'{timer.stop():.2f}sec' # 计时器停止时,停止与开始的时间间隔事件
加载数据集
%matplotlib inline
import torch
import torchvision
from torch.utils import data
from torchvision import transforms
from d2l import torch as d2l
d2l.use_svg_display()
# 通过ToTensor实例将图像数据从PIL类型变换成32位浮点数格式
# 并除以255使得所有像素的数值均在0到1之间
trans = transforms.ToTensor()
mnist_train = torchvision.datasets.FashionMNIST(root="01_data/01_DataSet_FashionMNIST",train=True,transform=trans,download=True)
mnist_test = torchvision.datasets.FashionMNIST(root="01_data/01_DataSet_FashionMNIST",train=False,transform=trans,download=True)
def get_fashion_mnist_labels(labels):
"""返回Fashion-MNIST数据集的文本标签"""
text_labels = ['t-shirt','trouser','pullover','dress','coat',
'sandal','shirt','sneaker','bag','ankle boot']
return [text_labels[int(i)] for i in labels]
def show_images(imgs, num_rows, num_cols, titles=None, scale=1.5):
"""Plot a list of images."""
figsize = (num_cols * scale, num_rows * scale) # 传进来的图像尺寸,scale 为放缩比例因子
_, axes = d2l.plt.subplots(num_rows,num_cols,figsize=figsize)
print(_)
print(axes) # axes 为构建的两行九列的画布
axes = axes.flatten()
print(axes) # axes 变成一维数据
for i,(ax,img) in enumerate(zip(axes,imgs)):
if torch.is_tensor(img):
# 图片张量
ax.imshow(img.numpy())
ax.set_title(titles[i])
else:
# PIL图片
ax.imshow(img)
X, y = next(iter(data.DataLoader(mnist_train,batch_size=18))) # X,y 为仅抽取一次的18个样本的图片、以及对应的标签值
show_images(X.reshape(18,28,28),2,9,titles=get_fashion_mnist_labels(y))
batch_size = 256
def get_dataloader_workers():
"""使用4个进程来读取的数据"""
return 4
train_iter = data.DataLoader(mnist_train, batch_size, shuffle=True,
num_workers=get_dataloader_workers())
timer = d2l.Timer()
for X,y in train_iter:
continue
f'{timer.stop():.2f}sec' # 扫一边数据集的事件
def load_data_fashion_mnist(batch_size, resize=None):
"""下载Fashion-MNIST数据集,然后将其加载到内存中"""
trans = [transforms.ToTensor()]
if resize:
trans.insert(0,transforms.Resize(resize)) # 如果有Resize参数传进来,就进行resize操作
trans = transforms.Compose(trans)
mnist_train = torchvision.datasets.FashionMNIST(root="01_data/01_DataSet_FashionMNIST",train=True,transform=trans,download=True)
mnist_test = torchvision.datasets.FashionMNIST(root="01_data/01_DataSet_FashionMNIST",train=False,transform=trans,download=True)
return (data.DataLoader(mnist_train, batch_size, shuffle=True, num_workers=get_dataloader_workers()),
data.DataLoader(mnist_train, batch_size, shuffle=True, num_workers=get_dataloader_workers()))
Softmax回归(从零开始实现)
① 就像从零开始实现线性回归一样,应该知道softmax的细节。
训练集、测试集抽取
import torch
from IPython import display
from d2l import torch as d2l
def load_data_fashion_mnist(batch_size, resize=None):
"""下载Fashion-MNIST数据集,然后将其加载到内存中"""
trans = [transforms.ToTensor()]
if resize:
trans.insert(0,transforms.Resize(resize)) # 如果有Resize参数传进来,就进行resize操作
trans = transforms.Compose(trans)
mnist_train = torchvision.datasets.FashionMNIST(root="01_data/01_DataSet_FashionMNIST",train=True,transform=trans,download=True)
mnist_test = torchvision.datasets.FashionMNIST(root="01_data/01_DataSet_FashionMNIST",train=False,transform=trans,download=True)
return (data.DataLoader(mnist_train, batch_size, shuffle=True, num_workers=get_dataloader_workers()),
data.DataLoader(mnist_train, batch_size, shuffle=True, num_workers=get_dataloader_workers()))
batch_size = 256
train_iter, test_iter = load_data_fashion_mnist(batch_size) # 返回训练集、测试集的迭代器
① 将展平每个图像,将它们视为长度784的向量。向量的每个元素与w相乘,所以w也需要784行。
② 因为数据集有10个类别,所以网络输出维度为10.
初始化参数
① 给定一个矩阵X,可以对所有元素求和。
import torch
from IPython import display
from d2l import torch as d2l
x = torch.tensor([[1.0,2.0,3.0],[4.0,5.0,6.0]])
print(x)
print(x.sum(0,keepdim=True)) # 按照列求和
print(x.sum(1,keepdim=True)) # 按照行求和
tensor([[1., 2., 3.],
[4., 5., 6.]])
tensor([[5., 7., 9.]])
tensor([[ 6.],
[15.]])
② 实现softmax:
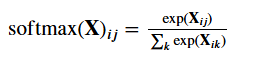
import torch
from IPython import display
from d2l import torch as d2l
def softmax(X):
X_exp = torch.exp(X) # 每个都进行指数运算
partition = X_exp.sum(1,keepdim=True)
return X_exp / partition # 这里应用了广播机制
# 将每个元素变成一个非负数。此外,依据概率原理,每行总和为1。
X = torch.normal(0,1,(2,5)) # 两行五列的数,数符合标准正态分布
print(X)
X_prob = softmax(X)
print(X_prob) # 形状没有发生变化,还是一个两行五列的矩阵,Softmax转换后所有值为正的
print(X_prob.sum(1)) # 相当于 X_prob.sum(axis=1) 按行求和,概率和为1
tensor([[ 1.6039, -0.1675, 0.8108, -0.1188, 0.9389],
[ 0.5993, 0.0179, -1.6758, 1.4489, -1.1852]])
tensor([[0.4319, 0.0735, 0.1954, 0.0771, 0.2221],
[0.2399, 0.1341, 0.0247, 0.5610, 0.0403]])
tensor([1., 1.])
定义模型
def net(X):
return softmax(torch.matmul(X.reshape((-1,w.shape[0])),w)+b) # -1为默认的批量大小,表示有多少个图片,每个图片用一维的784列个元素表示
交叉熵损失
① 创建一个数据y_hat,其中包含2个样本在3个类别的预测概率,使用y作为y_hat中概率的索引。
y = torch.tensor([0,2]) # 标号索引
y_hat = torch.tensor([[0.1,0.3,0.6],[0.3,0.2,0.5]]) # 两个样本在3个类别的预测概率
y_hat[[0,1],y] # 把第0个样本对应标号"0"的预测值拿出来、第1个样本对应标号"2"的预测值拿出来
tensor([0.1000, 0.5000])
实现交叉熵损失函数
def cross_entropy(y_hat, y):
print(list(range(len(y_hat))))
return -torch.log(y_hat[range(len(y_hat)),y]) # y_hat[range(len(y_hat)),y]为把y的标号列表对应的值拿出来。传入的y要是最大概率的标号
准确率
将预测类别与真实y元素进行比较。
import torch
from IPython import display
from d2l import torch as d2l
y = torch.tensor([0,2]) # 标号索引
y_hat = torch.tensor([[0.1,0.3,0.6],[0.3,0.2,0.5]]) # 两个样本在3个类别的预测概率
y_hat[[0,1],y] # 把第0个样本对应标号的预测值拿出来、第1个样本对应标号的预测值拿出来
print(y_hat.shape)
print(len(y_hat.shape)) # 两个样本
def accuracy(y_hat,y):
"""计算预测正确的数量"""
if len(y_hat.shape) > 1 and y_hat.shape[1] > 1: # y_hat.shape[1]>1表示不止一个类别,每个类别有各自的概率
y_hat = y_hat.argmax(axis=1) # y_hat.argmax(axis=1)为求行最大值的索引
print("y_hat:",y_hat)
cmp = y_hat.type(y.dtype) == y # 先判断逻辑运算符==,再赋值给cmp,cmp为布尔类型的数据
print("cmp:",cmp)
return float(cmp.type(y.dtype).sum()) # 获得y.dtype的类型作为传入参数,将cmp的类型转为y的类型(int型),然后再求和
print("accuracy(y_hat,y) / len(y):",accuracy(y_hat,y) / len(y))
print("accuracy(y_hat,y):",accuracy(y_hat,y))
print("len(y):",len(y))
torch.Size([2, 3])
2
y_hat: tensor([2, 2])
cmp: tensor([False, True])
accuracy(y_hat,y) / len(y): 0.5
y_hat: tensor([2, 2])
cmp: tensor([False, True])
accuracy(y_hat,y): 1.0
len(y): 2
任意模型
%matplotlib inline
import torch
import torchvision
from torch.utils import data
from torchvision import transforms
from d2l import torch as d2l
def get_dataloader_workers():
"""使用4个进程来读取的数据"""
return 4
def load_data_fashion_mnist(batch_size, resize=None):
"""下载Fashion-MNIST数据集,然后将其加载到内存中"""
trans = [transforms.ToTensor()]
if resize:
trans.insert(0,transforms.Resize(resize)) # 如果有Resize参数传进来,就进行resize操作
trans = transforms.Compose(trans)
mnist_train = torchvision.datasets.FashionMNIST(root="01_data/01_DataSet_FashionMNIST",train=True,transform=trans,download=True)
mnist_test = torchvision.datasets.FashionMNIST(root="01_data/01_DataSet_FashionMNIST",train=False,transform=trans,download=True)
return (data.DataLoader(mnist_train, batch_size, shuffle=True, num_workers=get_dataloader_workers()),
data.DataLoader(mnist_train, batch_size, shuffle=True, num_workers=get_dataloader_workers()))
batch_size = 256
train_iter, test_iter = load_data_fashion_mnist(batch_size) # 返回训练集、测试集的迭代器
num_inputs = 784
num_outputs = 10
w = torch.normal(0,0.01,size=(num_inputs,num_outputs),requires_grad=True)
b = torch.zeros(num_outputs,requires_grad=True)
def softmax(X):
X_exp = torch.exp(X) # 每个都进行指数运算
partition = X_exp.sum(1,keepdim=True)
return X_exp / partition # 这里应用了广播机制
# 实现softmax回归模型
def net(X):
return softmax(torch.matmul(X.reshape((-1,w.shape[0])),w)+b) # -1为默认的批量大小,表示有多少个图片,每个图片用一维的784列个元素表示
def cross_entropy(y_hat, y):
return -torch.log(y_hat[range(len(y_hat)),y]) # y_hat[range(len(y_hat)),y]为把y的标号列表对应的值拿出来。传入的y要是最大概率的标号
def accuracy(y_hat,y):
"""计算预测正确的数量"""
if len(y_hat.shape) > 1 and y_hat.shape[1] > 1: # y_hat.shape[1]>1表示不止一个类别,每个类别有各自的概率
y_hat = y_hat.argmax(axis=1) # y_hat.argmax(axis=1)为求行最大值的索引
cmp = y_hat.type(y.dtype) == y # 先判断逻辑运算符==,再赋值给cmp,cmp为布尔类型的数据
return float(cmp.type(y.dtype).sum()) # 获得y.dtype的类型作为传入参数,将cmp的类型转为y的类型(int型),然后再求和
# 可以评估在任意模型net的准确率
def evaluate_accuracy(net,data_iter):
"""计算在指定数据集上模型的精度"""
if isinstance(net,torch.nn.Module): # 如果net模型是torch.nn.Module实现的神经网络的话,将它变成评估模式
net.eval() # 将模型设置为评估模式
metric = Accumulator(2) # 正确预测数、预测总数,metric为累加器的实例化对象,里面存了两个数
for X, y in data_iter:
metric.add(accuracy(net(X),y),y.numel()) # net(X)将X输入模型,获得预测值。y.numel()为样本总数
return metric[0] / metric[1] # 分类正确的样本数 / 总样本数
# Accumulator实例中创建了2个变量,用于分别存储正确预测的数量和预测的总数量
class Accumulator:
"""在n个变量上累加"""
def __init__(self,n):
self.data = [0,0] * n
def add(self, *args):
self.data = [a+float(b) for a,b in zip(self.data,args)] # zip函数把两个列表第一个位置元素打包、第二个位置元素打包....
def reset(self):
self.data = [0.0] * len(self.data)
def __getitem__(self,idx):
return self.data[idx]
print(evaluate_accuracy(net, test_iter))
0.09536666666666667
训练函数
# 训练函数
def train_epoch_ch3(net, train_iter, loss, updater):
if isinstance(net, torch.nn.Module):
net.train() # 开启训练模式
metric = Accumulator(3)
for X, y in train_iter:
y_hat = net(X)
l = loss(y_hat,y) # 计算损失
if isinstance(updater, torch.optim.Optimizer): # 如果updater是pytorch的优化器的话
updater.zero_grad()
l.backward()
updater.step()
metric.add(float(l)*len(y),accuracy(y_hat,y),y.size().numel()) # 总的训练损失、样本正确数、样本总数
else:
l.sum().backward()
updater(X.shape[0])
metric.add(float(l.sum()),accuracy(y_hat,y),y.numel())
return metric[0] / metric[2], metric[1] / metric[2] # 所有loss累加除以样本总数,总的正确个数除以样本总数
动画绘制
%matplotlib inline
import torch
import torchvision
from torch.utils import data
from torchvision import transforms
from d2l import torch as d2l
class Animator:
def __init__(self, xlabel=None, ylabel=None, legend=None, xlim=None,
ylim=None, xscale='linear',yscale='linear',
fmts=('-','m--','g-.','r:'),nrows=1,ncols=1,
figsize=(3.5,2.5)):
if legend is None:
legend = []
d2l.use_svg_display()
self.fig, self.axes = d2l.plt.subplots(nrows,ncols,figsize=figsize)
if nrows * ncols == 1:
self.axes = [self.axes,]
self.config_axes = lambda: d2l.set_axes(self.axes[0],xlabel,ylabel,xlim,ylim,xscale,yscale,legend)
self.X, self.Y, self.fmts = None, None, fmts
def add(self, x, y):
if not hasattr(y, "__len__"):
y = [y]
n = len(y)
if not hasattr(x, "__len__"):
x = [x] * n
if not self.X:
self.X = [[] for _ in range(n)]
if not self.Y:
self.Y = [[] for _ in range(n)]
for i, (a,b) in enumerate(zip(x,y)):
if a is not None and b is not None:
self.X[i].append(a)
self.Y[i].append(b)
self.axes[0].cla()
for x, y, fmt in zip(self.X, self.Y, self.fmts):
self.axes[0].plot(x, y, fmt)
self.config_axes()
display.display(self.fig)
display.clear_output(wait=True)
轮次总训练函数
import torch
import torchvision
from torch.utils import data
from torchvision import transforms
from d2l import torch as d2l
from IPython import display
import matplotlib.pyplot as plt
def get_dataloader_workers():
"""使用4个进程来读取的数据"""
return 0
def load_data_fashion_mnist(batch_size, resize=None):
"""下载Fashion-MNIST数据集,然后将其加载到内存中"""
trans = [transforms.ToTensor()]
if resize:
trans.insert(0, transforms.Resize(resize)) # 如果有Resize参数传进来,就进行resize操作
trans = transforms.Compose(trans)
mnist_train = torchvision.datasets.FashionMNIST(root="01_data/01_DataSet_FashionMNIST", train=True, transform=trans,
download=True)
mnist_test = torchvision.datasets.FashionMNIST(root="01_data/01_DataSet_FashionMNIST", train=False, transform=trans,
download=True)
return (data.DataLoader(mnist_train, batch_size, shuffle=True, num_workers=get_dataloader_workers()),
data.DataLoader(mnist_train, batch_size, shuffle=True, num_workers=get_dataloader_workers()))
batch_size = 256
train_iter, test_iter = load_data_fashion_mnist(batch_size) # 返回训练集、测试集的迭代器
num_inputs = 784
num_outputs = 10
w = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)
b = torch.zeros(num_outputs, requires_grad=True)
def softmax(X):
X_exp = torch.exp(X) # 每个都进行指数运算
partition = X_exp.sum(1, keepdim=True)
return X_exp / partition # 这里应用了广播机制
# 实现softmax回归模型
def net(X):
return softmax(torch.matmul(X.reshape((-1, w.shape[0])), w) + b) # -1为默认的批量大小,表示有多少个图片,每个图片用一维的784列个元素表示
def cross_entropy(y_hat, y):
return -torch.log(y_hat[range(len(y_hat)), y]) # y_hat[range(len(y_hat)),y]为把y的标号列表对应的值拿出来。传入的y要是最大概率的标号
def accuracy(y_hat, y):
"""计算预测正确的数量"""
if len(y_hat.shape) > 1 and y_hat.shape[1] > 1: # y_hat.shape[1]>1表示不止一个类别,每个类别有各自的概率
y_hat = y_hat.argmax(axis=1) # y_hat.argmax(axis=1)为求行最大值的索引
cmp = y_hat.type(y.dtype) == y # 先判断逻辑运算符==,再赋值给cmp,cmp为布尔类型的数据
return float(cmp.type(y.dtype).sum()) # 获得y.dtype的类型作为传入参数,将cmp的类型转为y的类型(int型),然后再求和
# 可以评估在任意模型net的准确率
def evaluate_accuracy(net, data_iter):
"""计算在指定数据集上模型的精度"""
if isinstance(net, torch.nn.Module): # 如果net模型是torch.nn.Module实现的神经网络的话,将它变成评估模式
net.eval() # 将模型设置为评估模式
metric = Accumulator(2) # 正确预测数、预测总数,metric为累加器的实例化对象,里面存了两个数
for X, y in data_iter:
metric.add(accuracy(net(X), y), y.numel()) # net(X)将X输入模型,获得预测值。y.numel()为样本总数
return metric[0] / metric[1] # 分类正确的样本数 / 总样本数
# Accumulator实例中创建了2个变量,用于分别存储正确预测的数量和预测的总数量
class Accumulator:
"""在n个变量上累加"""
def __init__(self, n):
self.data = [0, 0] * n
def add(self, *args):
self.data = [a + float(b) for a, b in zip(self.data, args)] # zip函数把两个列表第一个位置元素打包、第二个位置元素打包....
def reset(self):
self.data = [0.0] * len(self.data)
def __getitem__(self, idx):
return self.data[idx]
# 训练函数
def train_epoch_ch3(net, train_iter, loss, updater):
if isinstance(net, torch.nn.Module):
net.train() # 开启训练模式
metric = Accumulator(3)
for X, y in train_iter:
y_hat = net(X)
l = loss(y_hat, y) # 计算损失
if isinstance(updater, torch.optim.Optimizer): # 如果updater是pytorch的优化器的话
updater.zero_grad()
l.mean().backward() # 这里对loss取了平均值出来
updater.step()
metric.add(float(l) * len(y), accuracy(y_hat, y), y.size().numel()) # 总的训练损失、样本正确数、样本总数
else:
l.sum().backward()
updater(X.shape[0])
metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
return metric[0] / metric[2], metric[1] / metric[2] # 所有loss累加除以样本总数,总的正确个数除以样本总数
class Animator:
def __init__(self, xlabel=None, ylabel=None, legend=None, xlim=None,
ylim=None, xscale='linear', yscale='linear',
fmts=('-', 'm--', 'g-.', 'r:'), nrows=1, ncols=1,
figsize=(3.5, 2.5)):
if legend is None:
legend = []
d2l.use_svg_display()
self.fig, self.axes = d2l.plt.subplots(nrows, ncols, figsize=figsize)
if nrows * ncols == 1:
self.axes = [self.axes, ]
self.config_axes = lambda: d2l.set_axes(self.axes[0], xlabel, ylabel, xlim, ylim, xscale, yscale, legend)
self.X, self.Y, self.fmts = None, None, fmts
def add(self, x, y):
if not hasattr(y, "__len__"):
y = [y]
n = len(y)
if not hasattr(x, "__len__"):
x = [x] * n
if not self.X:
self.X = [[] for _ in range(n)]
if not self.Y:
self.Y = [[] for _ in range(n)]
for i, (a, b) in enumerate(zip(x, y)):
if a is not None and b is not None:
self.X[i].append(a)
self.Y[i].append(b)
self.axes[0].cla()
for x, y, fmt in zip(self.X, self.Y, self.fmts):
self.axes[0].plot(x, y, fmt)
self.config_axes()
display.display(self.fig)
display.clear_output(wait=True)
# 总训练函数
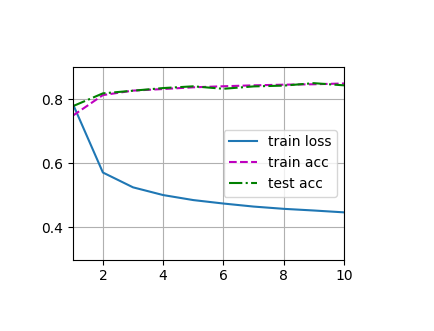
def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater):
animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],
legend=['train loss', 'train acc', 'test acc'])
for epoch in range(num_epochs): # 变量num_epochs遍数据
train_metrics = train_epoch_ch3(net, train_iter, loss, updater) # 返回两个值,一个总损失、一个总正确率
test_acc = evaluate_accuracy(net, test_iter) # 测试数据集上评估精度,仅返回一个值,总正确率
animator.add(epoch + 1, train_metrics + (test_acc,)) # train_metrics+(test_acc,) 仅将两个值的正确率相加,
train_loss, train_acc = train_metrics
# 小批量随即梯度下降来优化模型的损失函数
lr = 0.1
def updater(batch_size):
return d2l.sgd([w, b], lr, batch_size)
num_epochs = 10
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, updater)
plt.show()
预测数据
def predict_ch3(net,test_iter,n=6):
for X, y in test_iter:
break # 仅拿出一批六个数据
trues = d2l.get_fashion_mnist_labels(y)
preds = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1))
titles = [true + '\n' + pred for true, pred in zip(trues,preds)]
d2l.show_images(X[0:n].reshape((n,28,28)),1,n,titles=titles[0:n])
predict_ch3(net,test_iter)
Sofmax回归(使用框架)
import torch
from torch import nn
from d2l import torch as d2l
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
# Softmax回归的输出是一个全连接层
# PyTorch不会隐式地调整输入的形状
# 因此,我们定义了展平层(flatten)在线性层前调整网络输入的形状
net = nn.Sequential(nn.Flatten(),nn.Linear(784,10))
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01) # 方差为0.01
net.apply(init_weights)
print(net.apply(init_weights)) # net网络的参数用的是init_weights初始化参数
# 在交叉熵损失函数中传递未归一化的预测,并同时计算softmax及其对数
loss = nn.CrossEntropyLoss()
# 使用学习率为0.1的小批量随即梯度下降作为优化算法
trainer = torch.optim.SGD(net.parameters(),lr=0.1)
num_epochs = 10
d2l.train_ch3(net,train_iter,test_iter,loss,num_epochs,trainer)
多层感知机
单层感知机
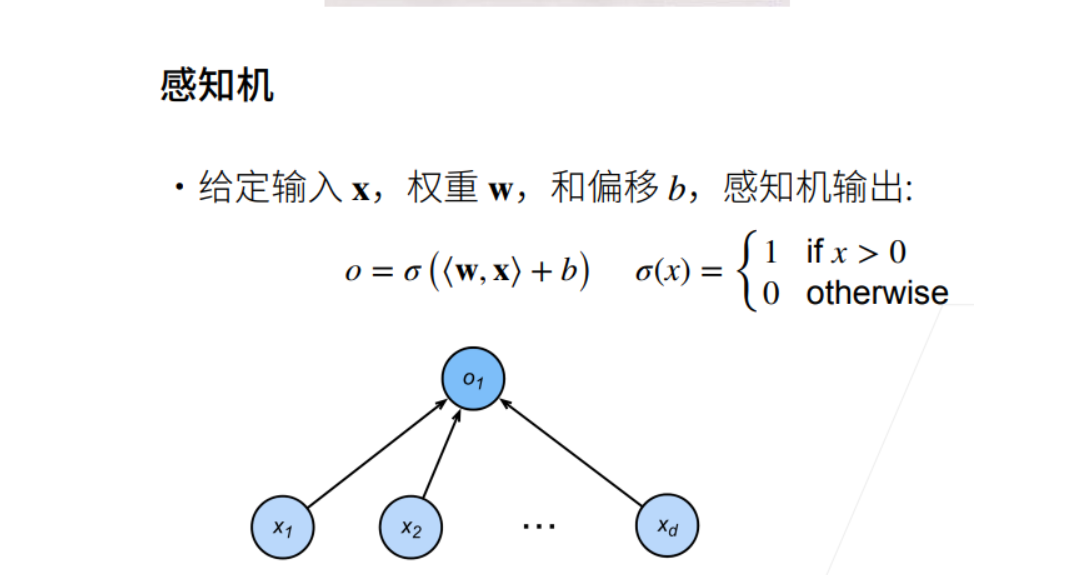
① 线性回归输出的是一个实数,感知机输出的是一个离散的类。

训练感知机
① 如果分类正确的话y<w,x>为正数,负号后变为一个负数,max后输出为0,则梯度不进行更新。
② 如果分类错了,y<w,x>为负数,下图中的if判断就成立了,就有梯度进行更新

收敛半径
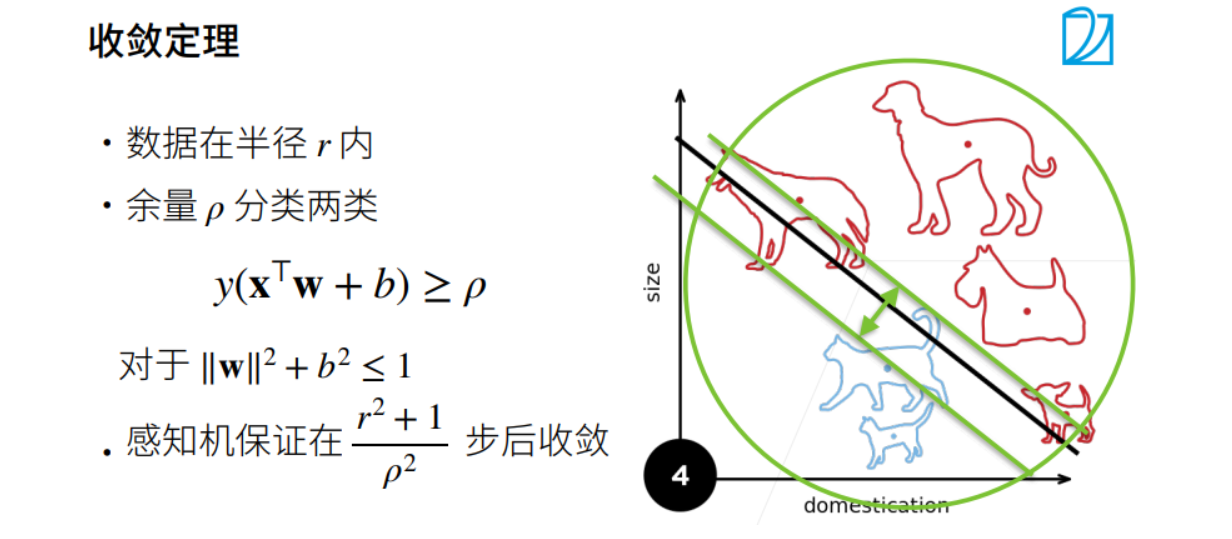
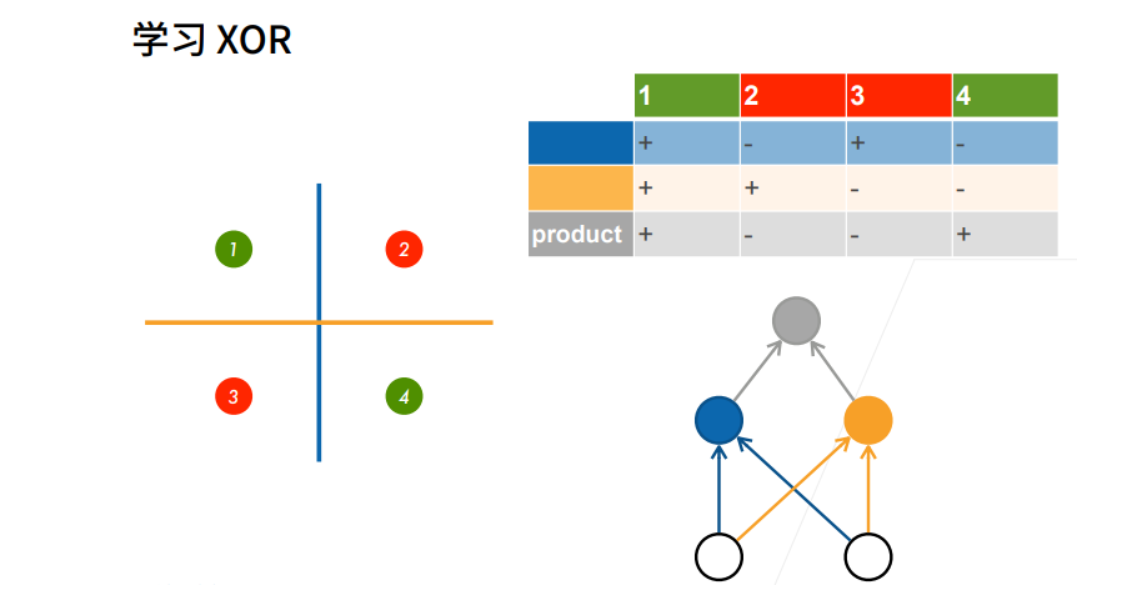
xor问题


多层感知机-xor
① 先用蓝色的线分,再用黄色的线分。
② 再对蓝色的线和黄色的线分出来的结果做乘法。
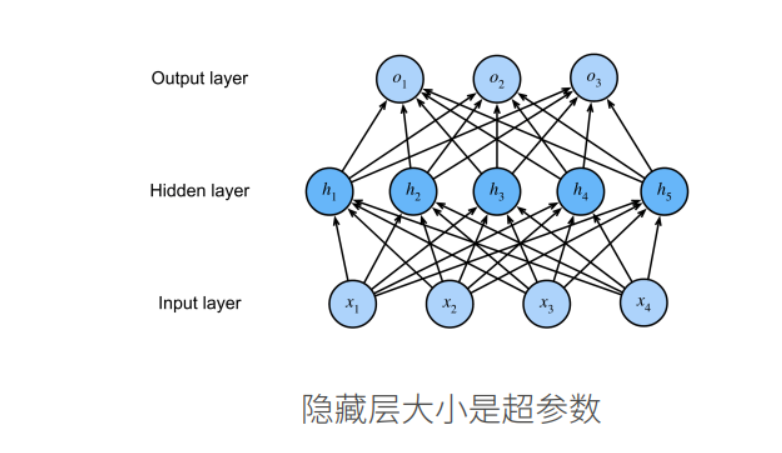
单隐藏层
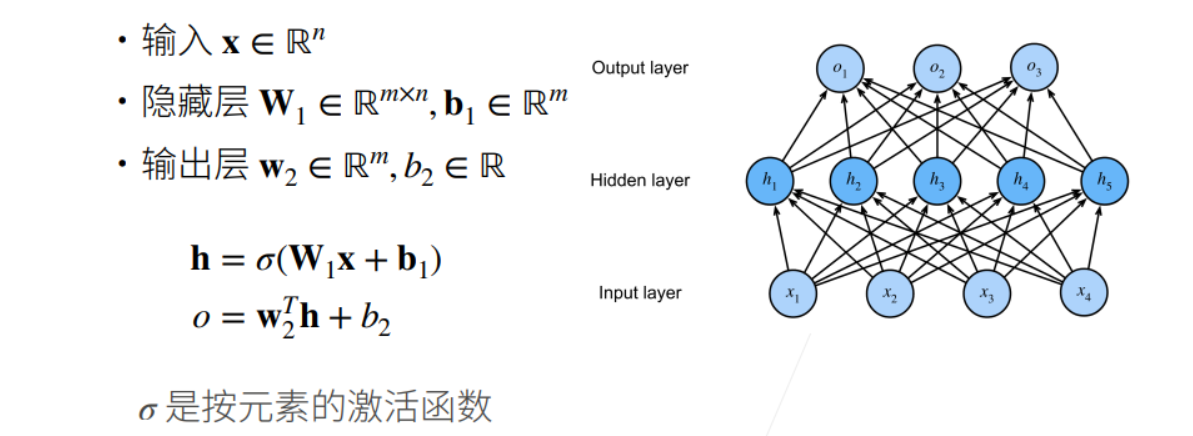
① 不用激活函数的话,所以全连接层连接在一起依旧可以用一个最简单的线性函数来表示。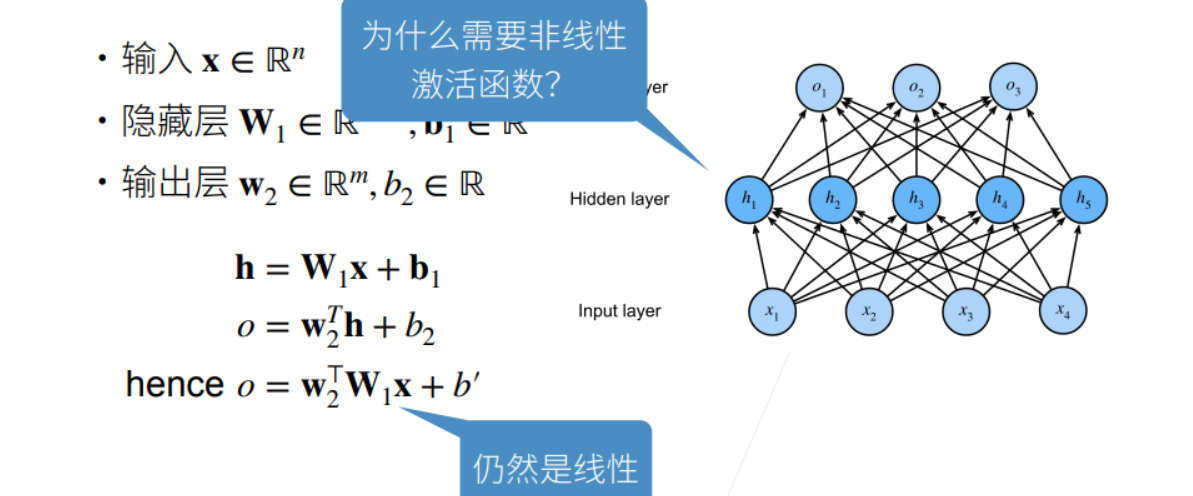
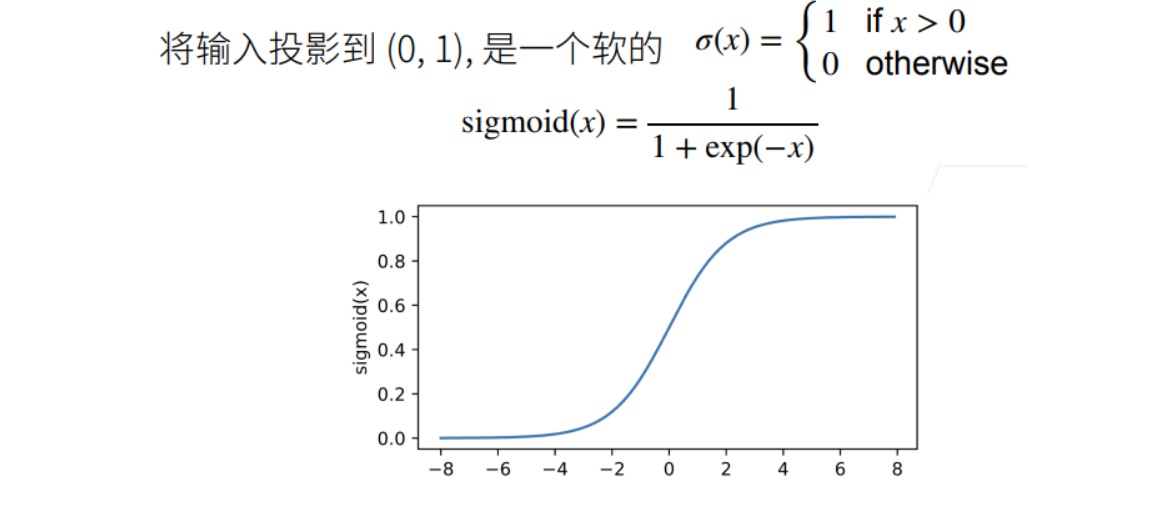
Sigmoid 函数
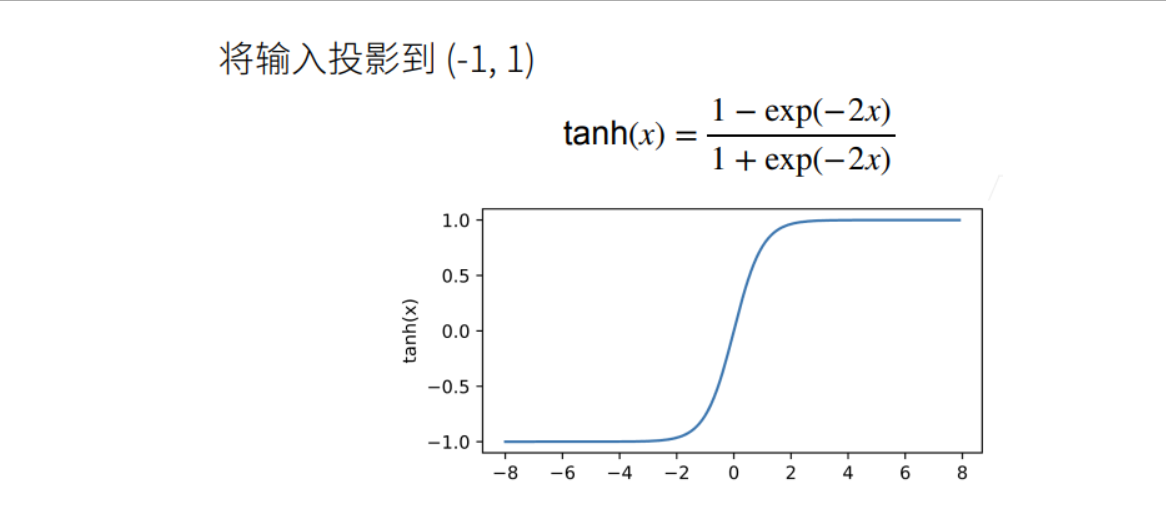
Tanh函数
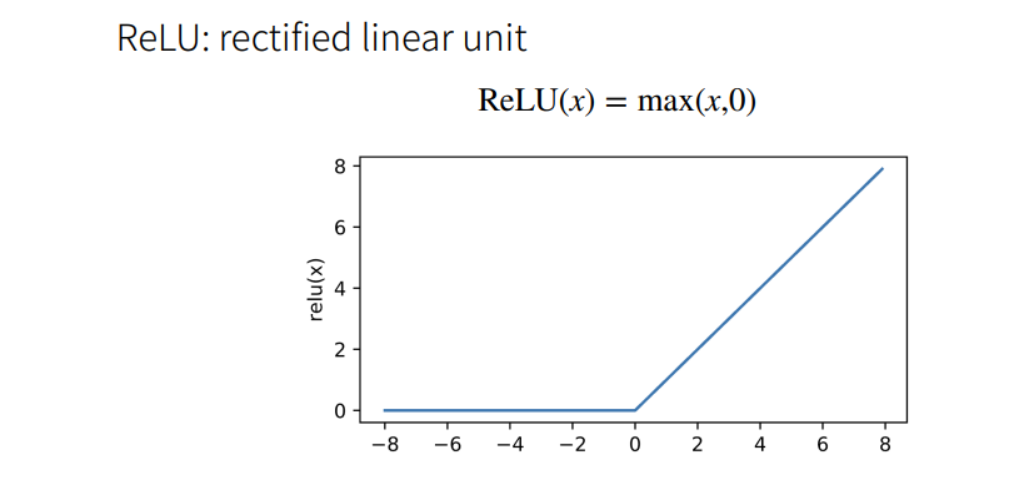
ReLU函数
① ReLU的好处在于不需要执行指数运算。
② 在CPU上一次指数运算相当于上百次乘法运算。

实现
import torch
from torch import nn
from d2l import torch as d2l
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
# 实现一个具有单隐藏层的多层感知机,它包含256个隐藏单元
num_inputs, num_outputs, num_hiddens = 784, 10, 256 # 输入、输出是数据决定的,256是调参自己决定的
W1 = nn.Parameter(torch.randn(num_inputs, num_hiddens, requires_grad=True))
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(num_hiddens, num_outputs, requires_grad=True))
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))
params = [W1,b1,W2,b2]
# 实现 ReLu 激活函数
def relu(X):
a = torch.zeros_like(X) # 数据类型、形状都一样,但是值全为 0
return torch.max(X,a)
# 实现模型
def net(X):
#print("X.shape:",X.shape)
X = X.reshape((-1, num_inputs)) # -1为自适应的批量大小
#print("X.shape:",X.shape)
H = relu(X @ W1 + b1)
#print("H.shape:",H.shape)
#print("W2.shape:",W2.shape)
return (H @ W2 + b2)
# 损失
loss = nn.CrossEntropyLoss() # 交叉熵损失
# 多层感知机的训练过程与softmax回归的训练过程完全一样
num_epochs ,lr = 30, 0.1
updater = torch.optim.SGD(params, lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)
实现(使用框架)
① 调用高级API更简洁地实现多层感知机。
import torch
from torch import nn
from d2l import torch as d2l
# 隐藏层包含256个隐藏单元,并使用了ReLU激活函数
net = nn.Sequential(nn.Flatten(),nn.Linear(784,256),nn.ReLU(),nn.Linear(256,10))
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight,std=0,)
net.apply(init_weights)
# 训练过程
batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss()
trainer = torch.optim.SGD(net.parameters(), lr=lr)
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
模型选择




过拟合、欠拟合
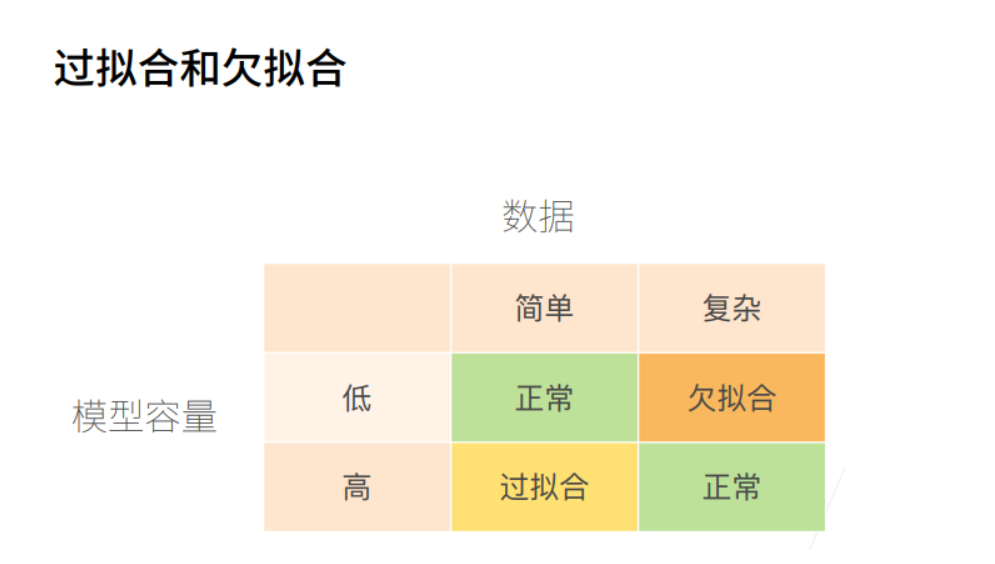
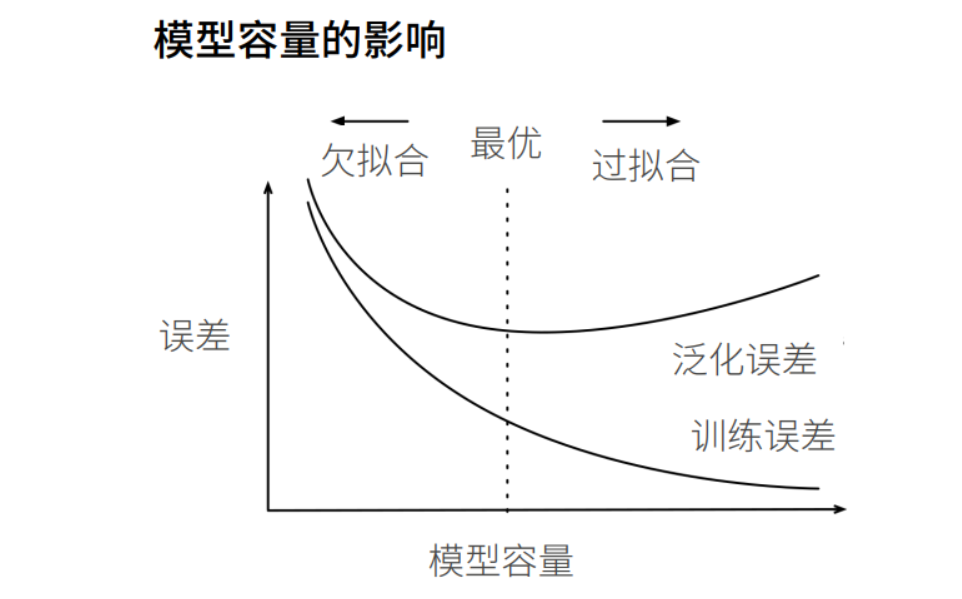
多项式解释欠拟合、过拟合
# 通过多项式拟合来交互地探索这些概念
import math
import numpy as np
import torch
from torch import nn
from d2l import torch as d2l
max_degree = 20 # 特征为20就是每一个样本是一个[20,1]的tensor
n_train, n_test = 100, 100 # 100个测试样本、100验证样本
true_w = np.zeros(max_degree)
true_w[0:4] = np.array([5,1.2,-3.4,5.6]) # 真实标号为5
features = np.random.normal(size=(n_train+n_test,1))
print(features.shape)
np.random.shuffle(features)
print(np.arange(max_degree))
print(np.arange(max_degree).reshape(1,-1))
print(np.power([[10,20]],[[1,2]]))
poly_features = np.power(features, np.arange(max_degree).reshape(1,-1)) # 对第所有维的特征取0次方、1次方、2次方...19次方
for i in range(max_degree):
poly_features[:,i] /= math.gamma(i+1) # i次方的特征除以(i+1)阶乘
labels = np.dot(poly_features,true_w) # 根据多项式生成y,即生成真实的labels
labels += np.random.normal(scale=0.1,size=labels.shape) # 对真实labels加噪音进去
#看一下前两个样本
true_w, features, poly_features, labels = [torch.tensor(x,dtype=torch.float32) for x in [true_w, features, poly_features, labels]]
print(features[:2]) # 前两个样本的x
print(poly_features[:2,:]) # 前两个样本的x的所有次方
print(labels[:2]) # 前两个样本的x对应的y
# 实现一个函数来评估模型在给定数据集上的损失
def evaluate_loss(net, data_iter, loss):
"""评估给定数据集上模型的损失"""
metric = d2l.Accumulator(2) # 两个数的累加器
for X, y in data_iter: # 从迭代器中拿出对应特征和标签
out = net(X)
y = y.reshape(out.shape) # 将真实标签改为网络输出标签的形式,统一形式
l = loss(out, y) # 计算网络输出的预测值与真实值之间的损失差值
metric.add(l.sum(), l.numel()) # 总量除以个数,等于平均
return metric[0] / metric[1] # 返回数据集的平均损失
# 定义训练函数
def train(train_features, test_features, train_labels, test_labels, num_epochs=400):
loss = nn.MSELoss()
input_shape = train_features.shape[-1]
net = nn.Sequential(nn.Linear(input_shape, 1, bias=False)) # 单层线性回归
batch_size = min(10,train_labels.shape[0])
train_iter = d2l.load_array((train_features,train_labels.reshape(-1,1)),batch_size)
test_iter = d2l.load_array((test_features,test_labels.reshape(-1,1)),batch_size,is_train=False)
trainer = torch.optim.SGD(net.parameters(),lr=0.01)
animator = d2l.Animator(xlabel='epoch',ylabel='loss',yscale='log',xlim=[1,num_epochs],ylim=[1e-3,1e2],legend=['train','test'])
for epoch in range(num_epochs):
d2l.train_epoch_ch3(net, train_iter, loss, trainer)
if epoch == 0 or (epoch + 1) % 20 == 0:
animator.add(epoch + 1, (evaluate_loss(net, train_iter, loss), evaluate_loss(net,test_iter,loss)))
print('weight',net[0].weight.data.numpy()) # 训练完后打印,打印最终学到的weight值
(200, 1)
[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19]
[[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19]]
[[ 10 400]]
tensor([[-0.9840],
[ 1.2229]])
tensor([[ 1.0000e+00, -9.8401e-01, 4.8414e-01, -1.5880e-01, 3.9065e-02,
-7.6880e-03, 1.2608e-03, -1.7724e-04, 2.1801e-05, -2.3836e-06,
2.3455e-07, -2.0981e-08, 1.7205e-09, -1.3023e-10, 9.1534e-12,
-6.0047e-13, 3.6929e-14, -2.1376e-15, 1.1685e-16, -6.0519e-18],
[ 1.0000e+00, 1.2229e+00, 7.4775e-01, 3.0481e-01, 9.3187e-02,
2.2792e-02, 4.6454e-03, 8.1155e-04, 1.2406e-04, 1.6856e-05,
2.0614e-06, 2.2917e-07, 2.3354e-08, 2.1969e-09, 1.9190e-10,
1.5645e-11, 1.1958e-12, 8.6019e-14, 5.8441e-15, 3.7614e-16]])
tensor([1.1747, 5.7716])
卷积层
从全连接到卷积

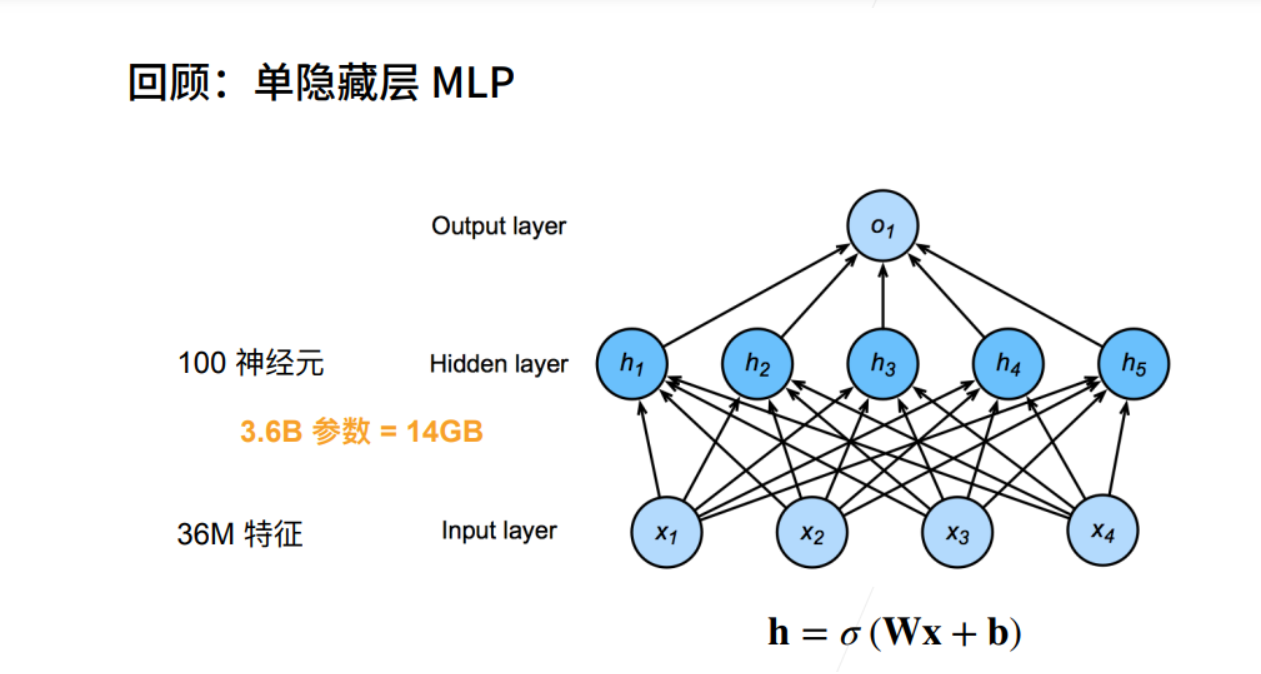

① k、l表示图片的第k行、第l列个像素,它相当于全连接层的 𝑥𝑖 , 𝑥𝑖 乘以一个权重值,得到全连接层中一层神经元中一个神经元的一条线的值。
② 有一个四维的W,里面有很多个w,例如前图的全连接层有100个w。i,j表示此w的坐标,即遍历所有的i、j合为100。每个w又是一个矩阵,每个w连接所有像素,对应矩阵宽高为k和l。因此下图中的 ℎ𝑖,𝑗为全连接层中一个神经元的输出。
③ 原来的k,l是基于图片的绝对位置,ab是根据ij的相对位置,这里就省略绝对位置,只需要一个原点加相对原点的相对位置,就可以表示位置信息。
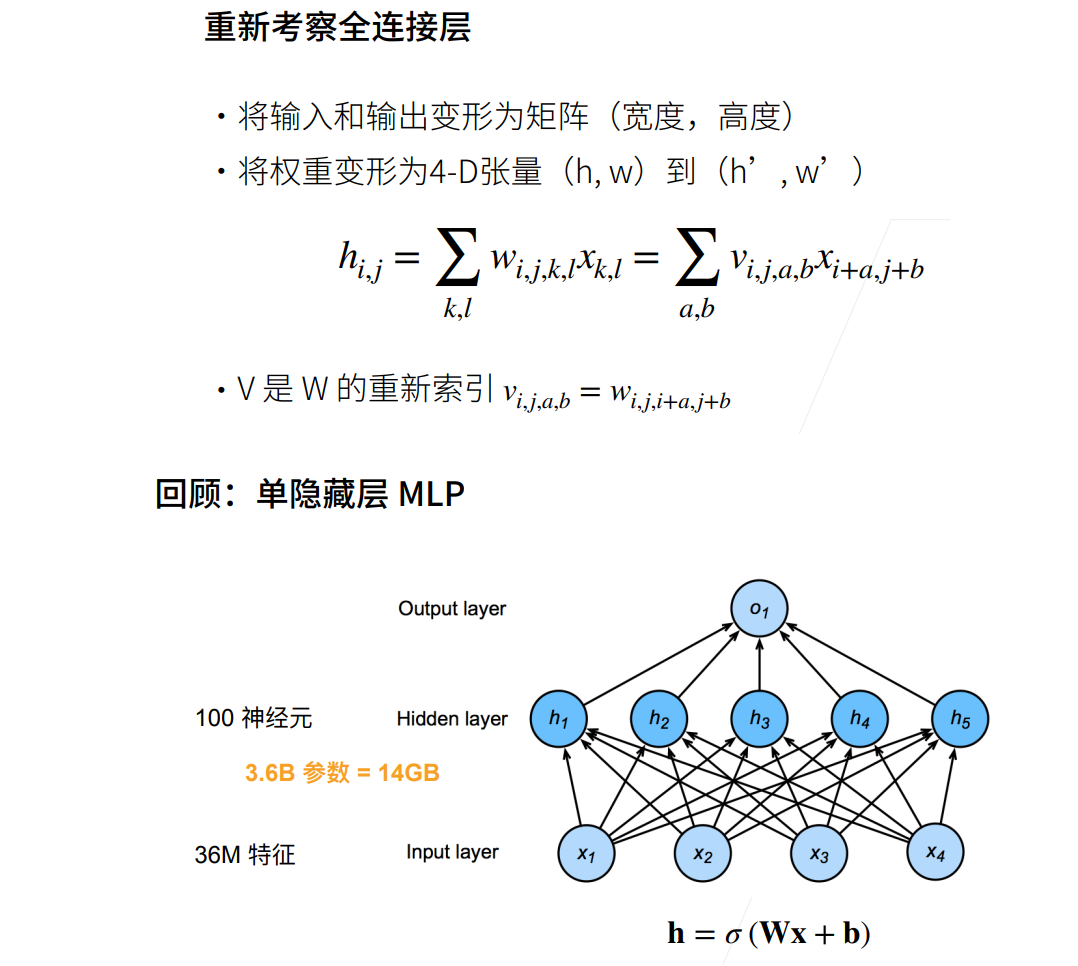
① 当在图片中形成一个识别器后,在一定像素大小的范围内,它都有自己的权重,当这个识别器在图片上换位置之后,它的权重应该不变。
② 理解成用同一张卷积核遍历整张图片。卷积核不会随着位置变化而变化。
③ 权重就是特征提取器,不应该随位置而发生变化。
④ 简而言之卷积核就是个框,在图片上不断扫描,无论扫在图上的哪个位置,卷积核都是不变的。
⑤ 对于一张图片应该有多个卷积核,但是每个卷积核要识别的东西不同,一个卷积核就是一个分类器。
⑥ 卷积确实是weight shared,但不是全联接,每个神经元是对应卷积核大小个输入。
⑦ 卷积就是weight shared全连接。






















 1981
1981

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








