群体智能优化算法-测试函数1（免费，代码可下载）

原创 已于 2025-03-28 11:12:19 修改 · 1.5k 阅读 · 15 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#算法 #matlab #群体智能优化 #优化 #机器学习

于 2025-03-28 11:09:51 首次发布

        为了验证群体智能优化算法的性能，研究者通常会在一组标准化的测试函数上进行实验。这些函数具有明确的数学性质，如多峰性、非线性、约束性等，能够全面衡量算法的搜索能力和收敛性能。本文整理了20个经典的优化测试函数，并提供了统一接口函数和对应目标函数定义，适用于算法开发与比较实验。

一、模块功能介绍

该模块主要由以下两部分构成：

  1. Get_Functions_details(F)：根据输入的编号（如 'F1'、'F2'），返回该测试函数的：

    • 函数句柄 fobj
    • 搜索空间下界 lb
    • 上界 ub
    • 变量维度 dim

  2. 一组已定义的测试函数 F1 ~ F20，均封装为匿名函数格式，可直接用于优化算法调用。

使用方式简单，例如：

[lb, ub, dim, fobj] = Get_Functions_details('F11');  % 获取Rastrigin函数配置

二、常用测试函数列表与说明

编号函数名称特性维度搜索范围
F1Schwefel-like多峰函数30[-600, 600]
F2绝对值+乘积函数多峰，非凸30[-10, 10]
F3Shekel’s Foxholes多极值，二维2[-65.536, 65.536]
F4最大绝对值函数单峰函数30[-100, 100]
F5Rosenbrock非线性单谷函数30[-30, 30]
F6Branin多极值函数2[-5, 20]
F7有约束惩罚函数含惩罚项30[-100, 100]
F8不等式约束函数带不等式约束3[0, 1]
F9等式约束函数带等式约束3[0, 2]
F10Sphere简单凸函数30[-100, 100]
F11Rastrigin多峰函数30[-5.12, 5.12]
F12Griewank多峰，复杂形状30[-600, 600]
F13Ackley多极值，难收敛30[-32, 32]
F14Zakharov单峰30[-5, 10]
F15Levy多极值函数10[-10, 10]
F16Schaffer N.2非常尖锐的函数2[-100, 100]
F17Eggholder非常复杂多峰2[-512, 512]
F18Drop-Wave多峰，波动型2[-5.12, 5.12]
F19Schwefel多峰，全局最优远离原点30[-500, 500]
F20Michalewicz非常复杂10[0, π]

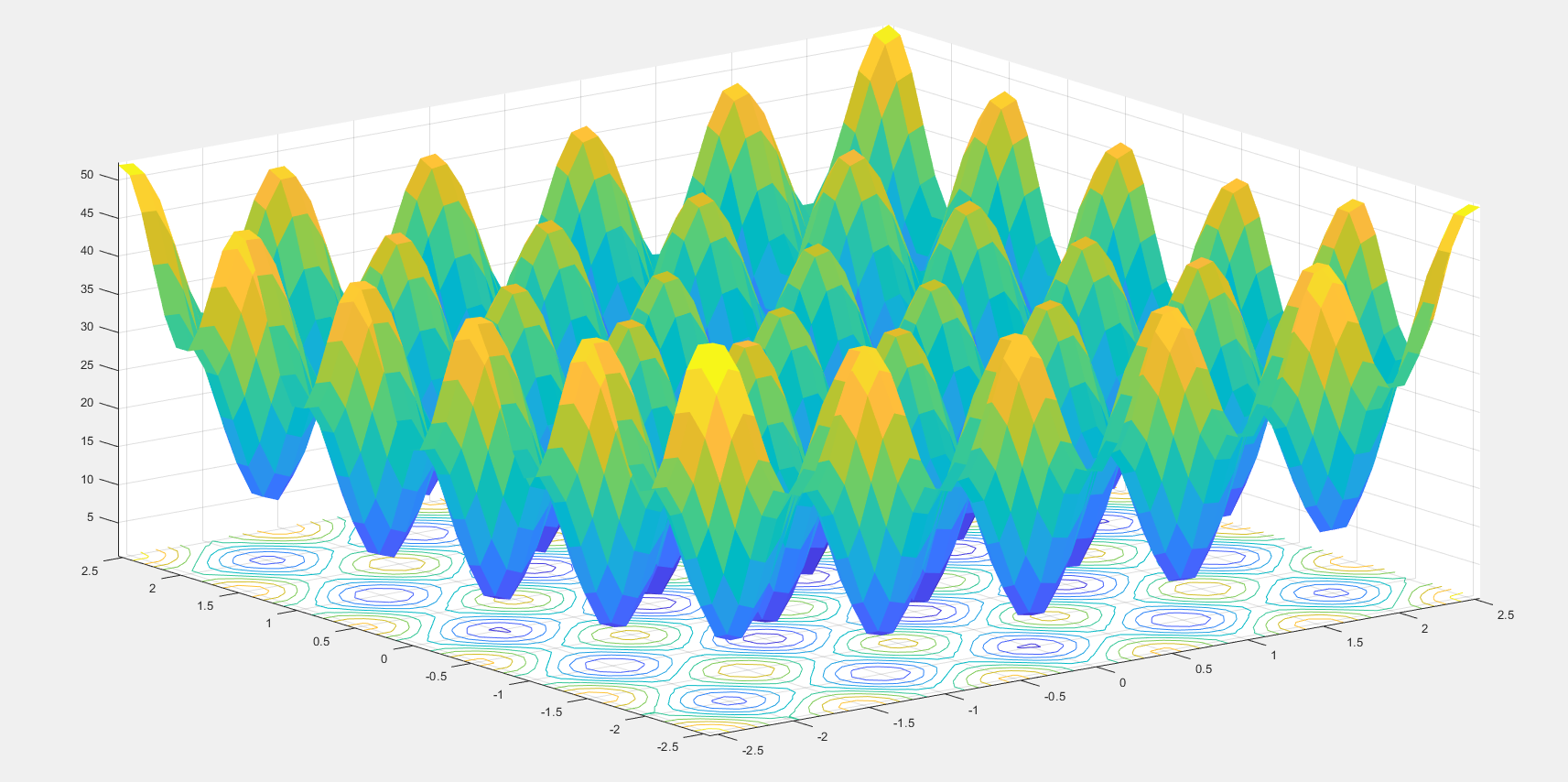
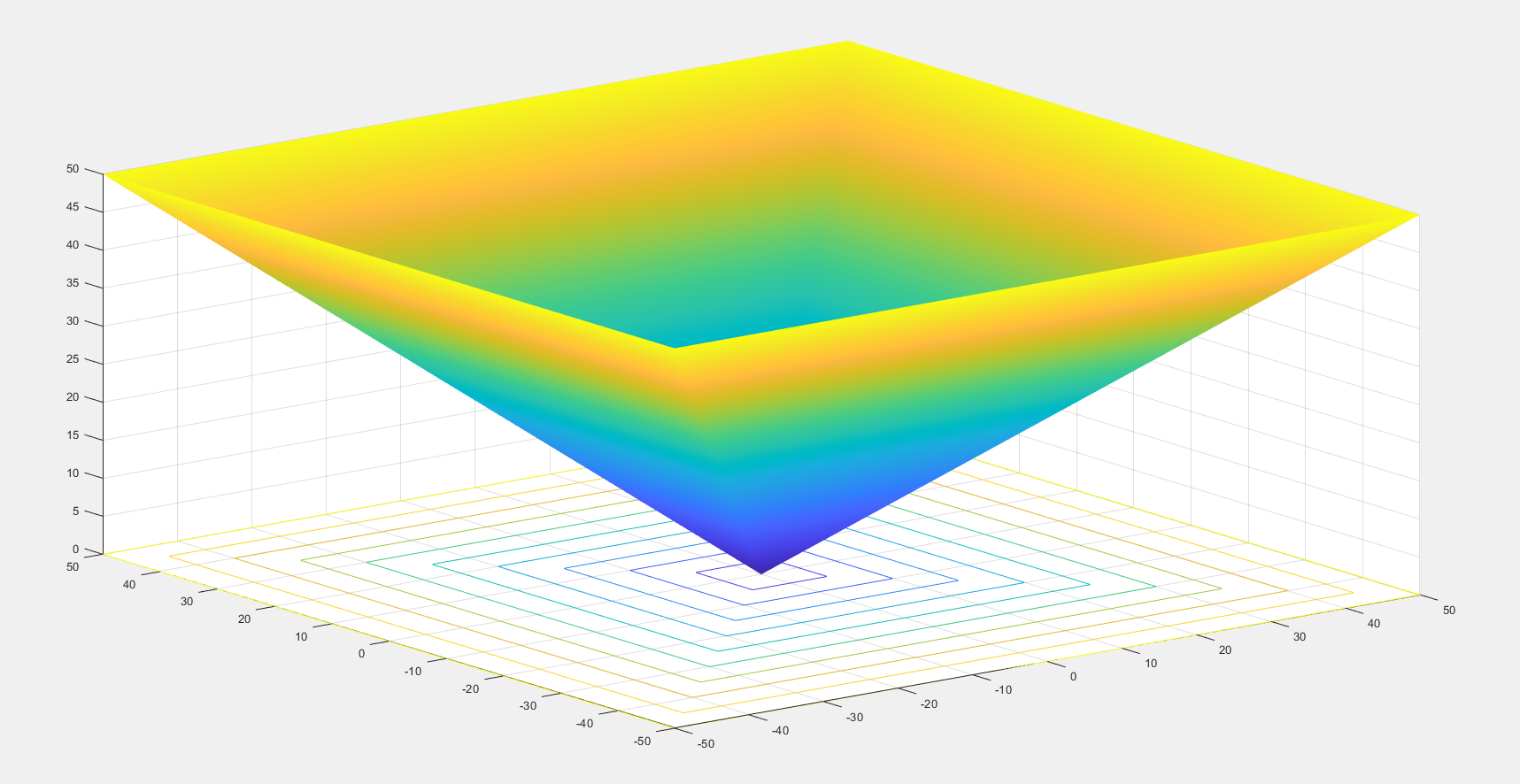
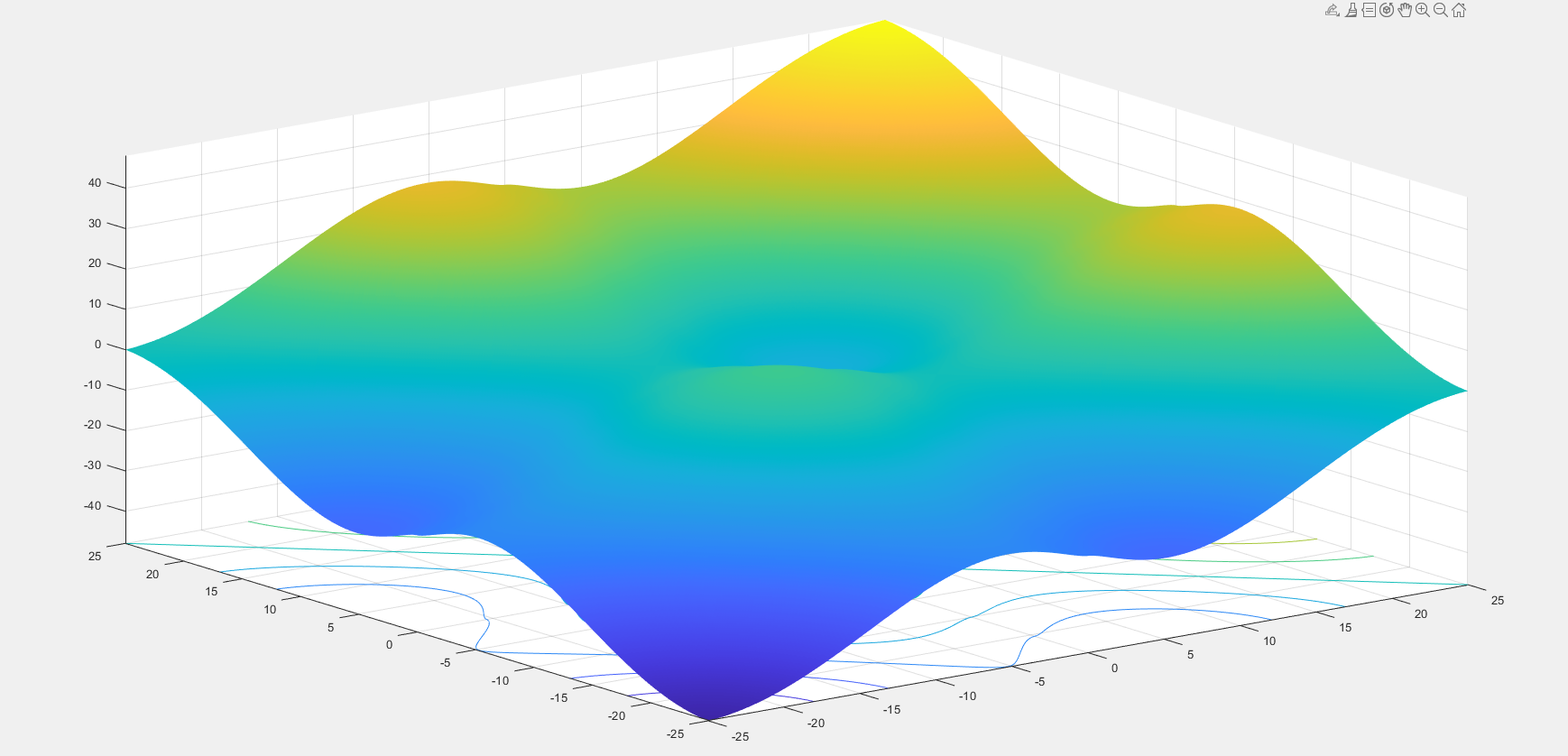
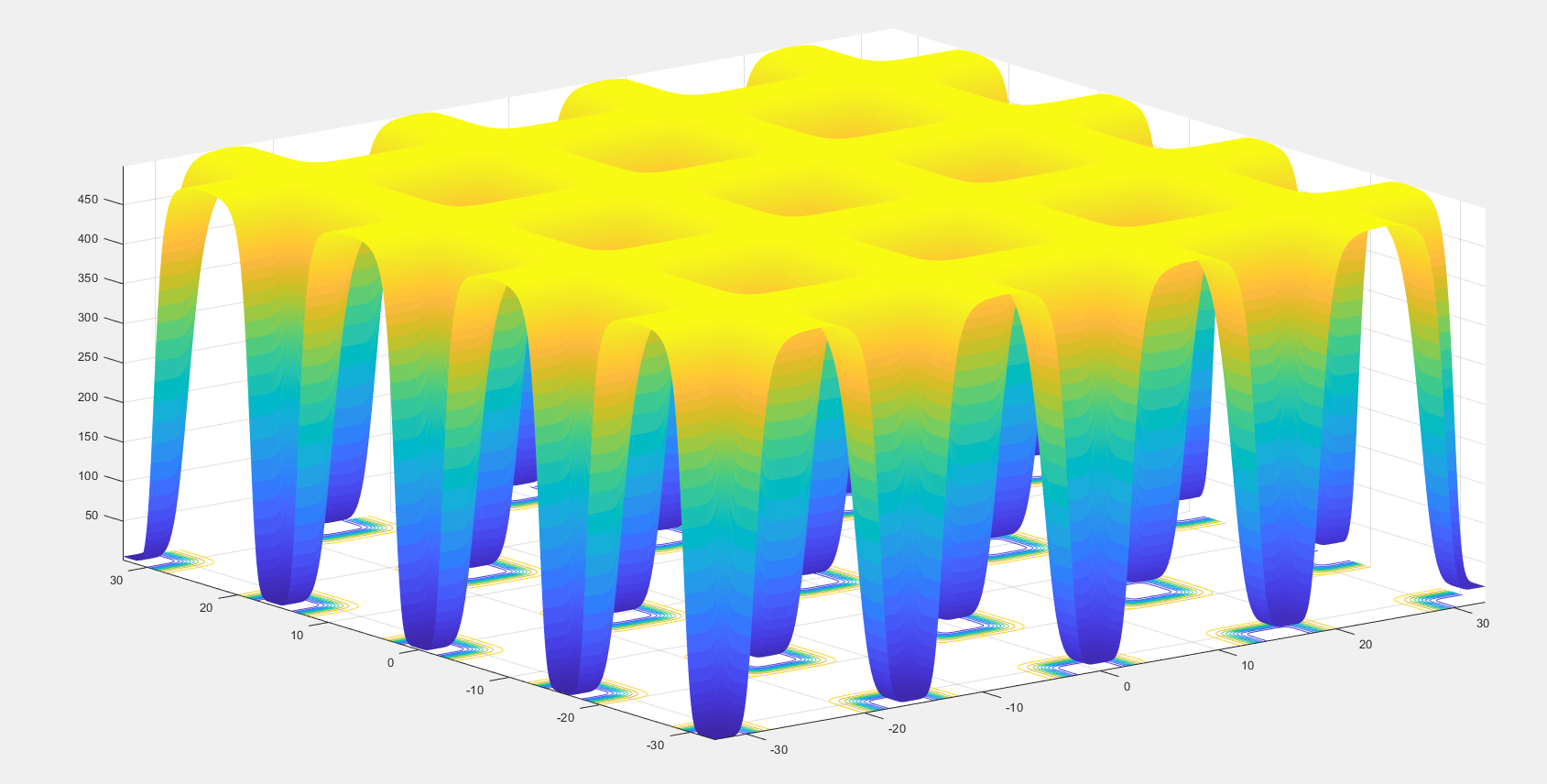
部分测试函数示例：

 

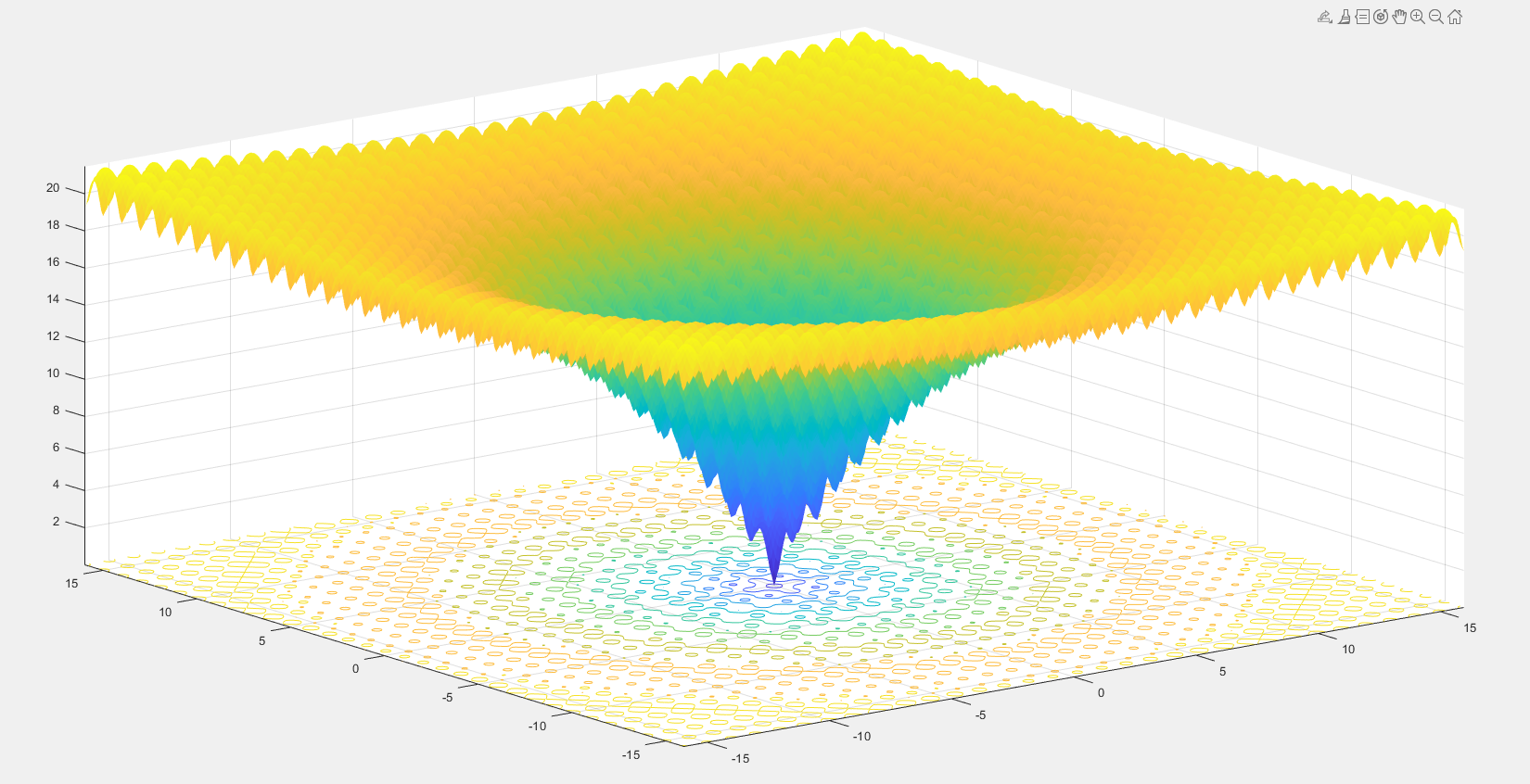
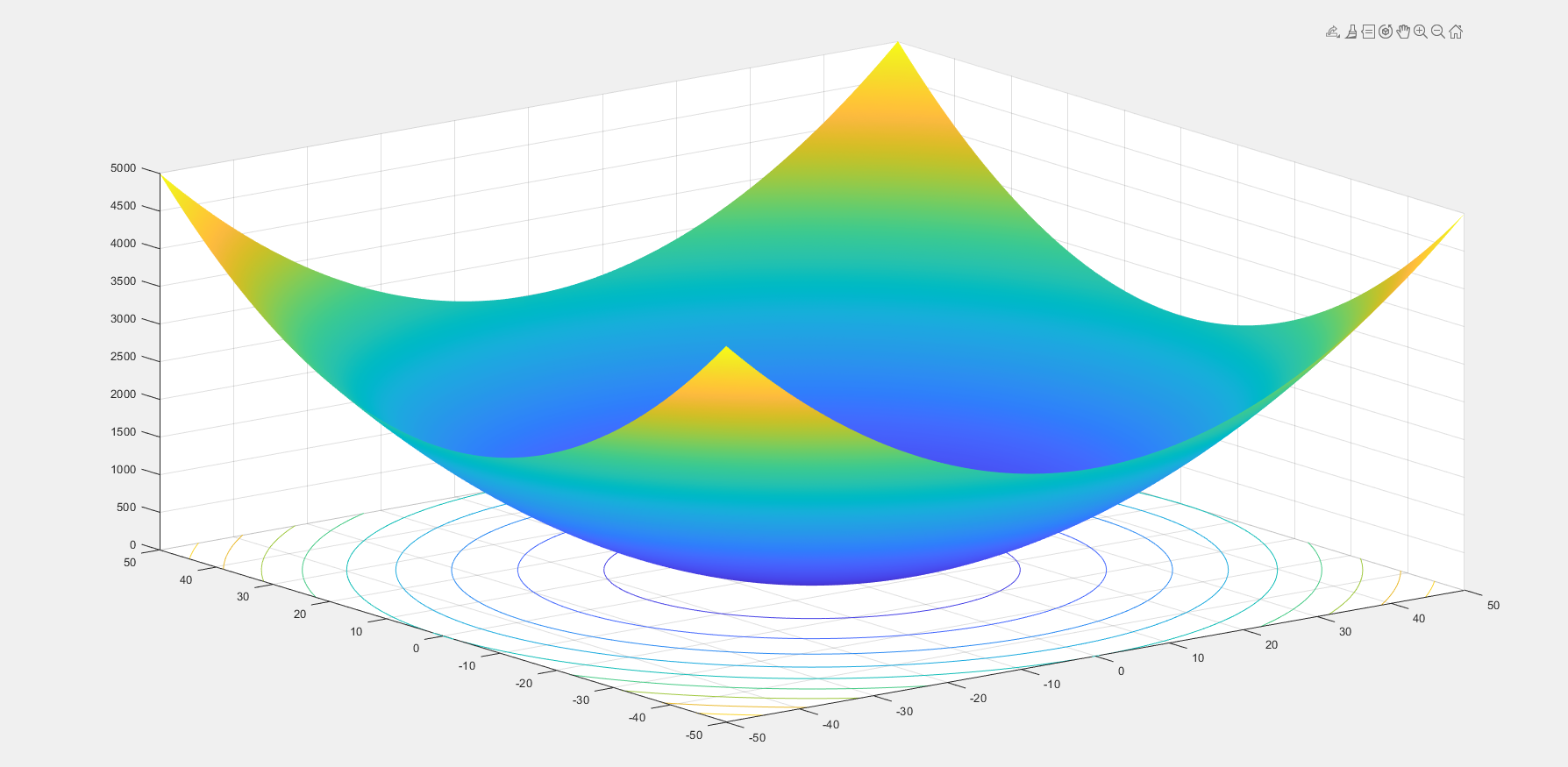
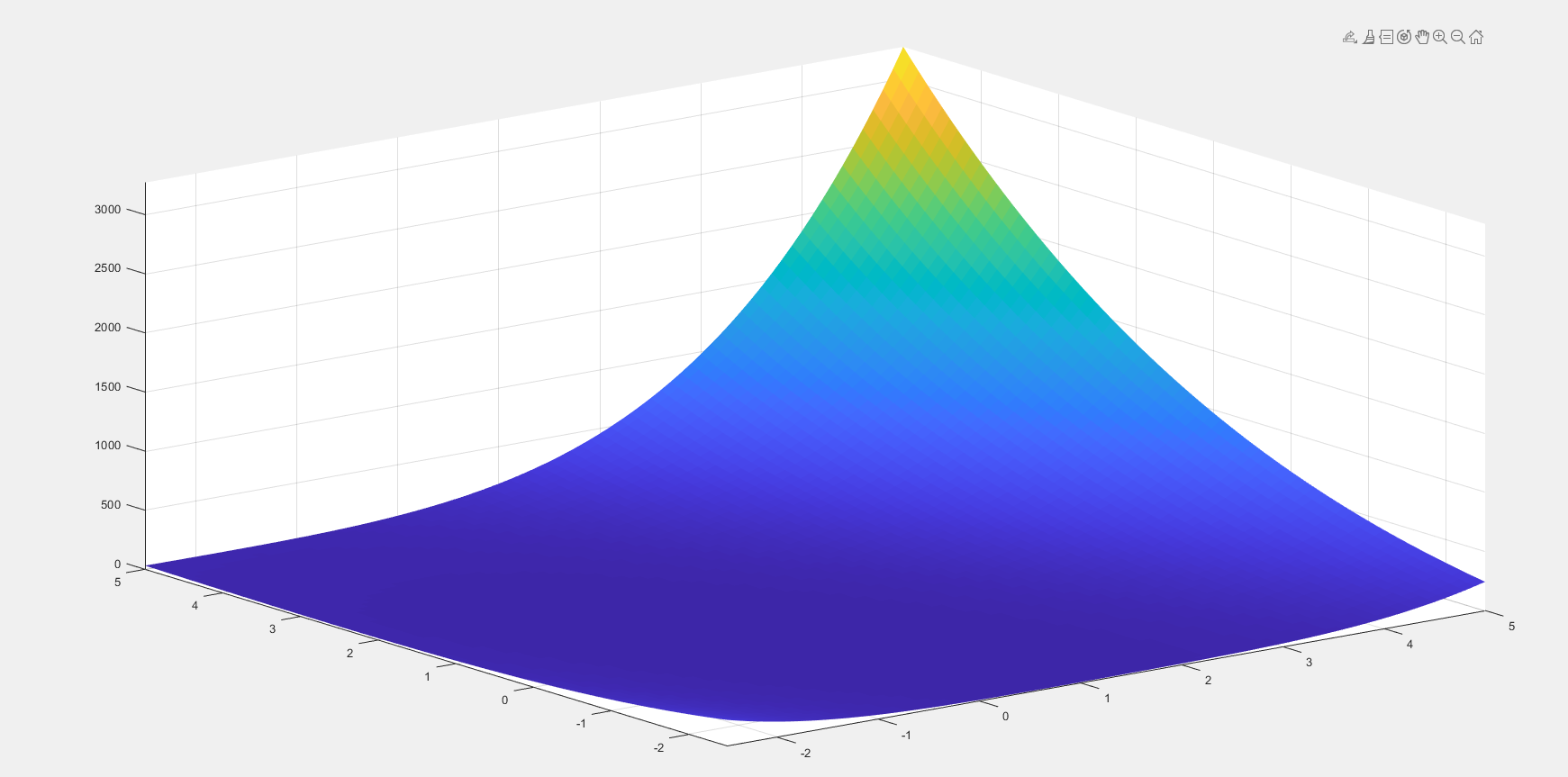
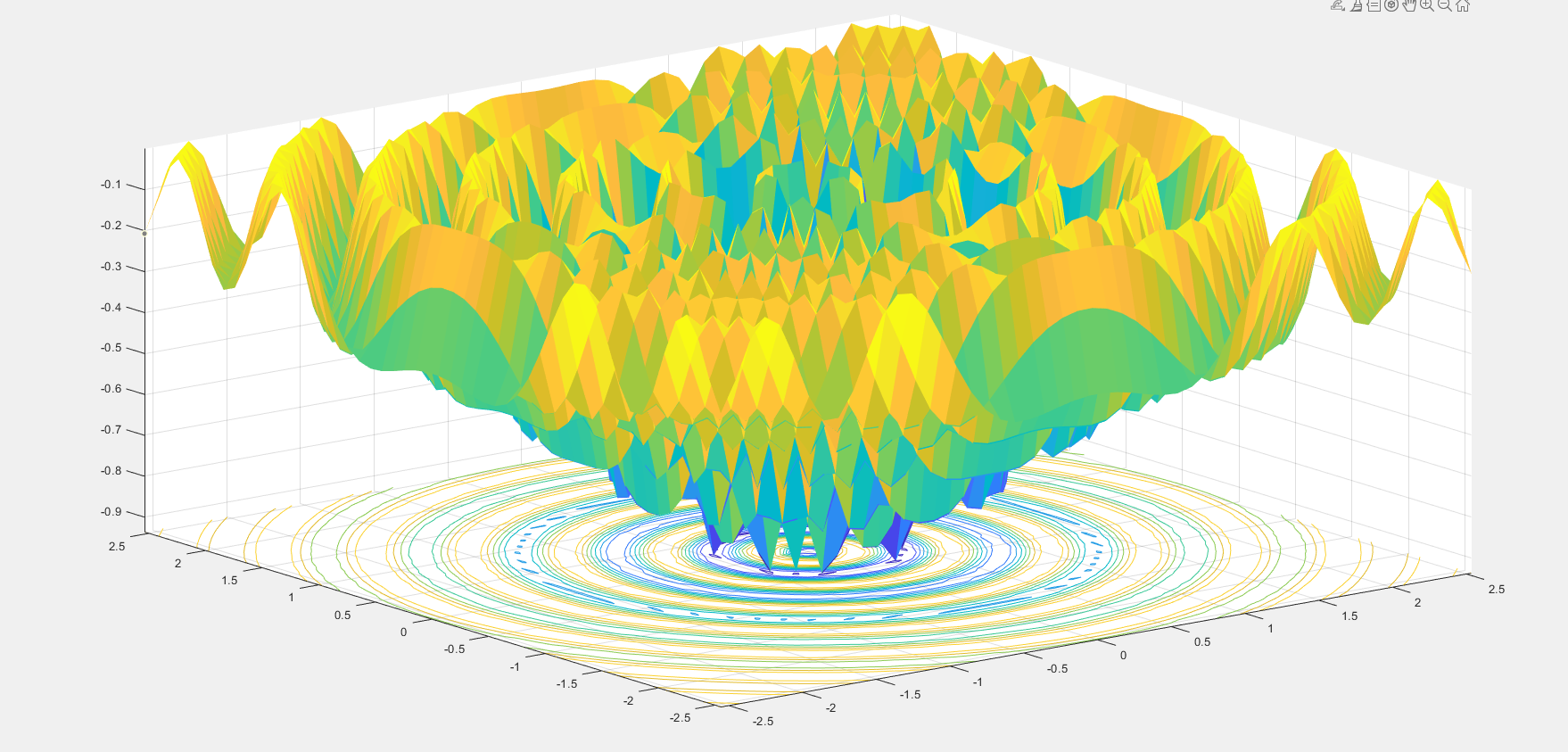
三、函数结构说明

1. 主函数

该函数根据输入字符串 'F1' ~ 'F20'，输出目标函数的配置信息和对应函数句柄，方便统一调用。示例：

function [lb,ub,dim,fobj] = Get_Functions_details(F)
    switch F
        case 'F11'
            fobj = @F11;
            lb = -5.12;
            ub = 5.12;
            dim = 30;
        ...
    end
end

2. 测试函数定义示例：

function o = F10(x)  % Sphere函数
    o = sum(x.^2);    % 函数最优值为0，x=0时取得
end

function o = F13(x)  % Ackley函数
    o = -20*exp(-0.2*sqrt(mean(x.^2))) - exp(mean(cos(2*pi*x))) + 20 + exp(1);
end

function o = F19(x)  % Schwefel函数
    o = 418.9829*length(x) - sum(x .* sin(sqrt(abs(x))));
end

3. 约束函数示例：

function o = F7(x)
    o = sum(abs((x + 0.5)).^2);
    g1 = ... % 约束1
    g2 = ... % 约束2
    o = o + 10000*(g1 + g2);  % 惩罚项
end

四、如何使用本模块进行算法测试

1. 获取测试函数信息

[F_lb, F_ub, F_dim, F_fobj] = Get_Functions_details('F15');

2. 在优化算法中调用：假设你有一个算法函数 MyOptimizer，可以这样写：

[bestScore, bestSol] = MyOptimizer(F_fobj, F_dim, F_lb, F_ub, 100, 500);

3. 记录收敛曲线、可视化结果等

五、完整代码

function [lb,ub,dim,fobj] = Get_Functions_details(F)
% 此函数用于根据输入的函数编号F，返回对应的测试函数句柄fobj，
% 以及该函数的变量下界lb、上界ub和维度dim。
% 在群体智能优化算法中用于统一测试平台。

switch F
    case 'F1'              % Griewank函数
        fobj = @F12;
        lb = -600;
        ub = 600;
        dim = 30;

    case 'F2'              % Ackley函数
        fobj = @F13;
        lb = -32;
        ub = 32;
        dim = 30;

    case 'F3'              % Sphere函数
        fobj = @F10;
        lb = -100;
        ub = 100;
        dim = 30;

    case 'F4'              % Zakharov函数
        fobj = @F14;
        lb = -5;
        ub = 10;
        dim = 30;

    case 'F5'              % 带约束的函数
        fobj = @F9;
        lb = [0,0,0];
        ub = 2.*[1,1,1];
        dim = 3;

    case 'F6'              % 带约束的函数
        fobj = @F7;
        lb = -100;
        ub = 100;
        dim = 30;

    case 'F7'              % F2函数（abs+prod）
        fobj = @F2;
        lb = -10;
        ub = 10;
        dim = 30;

    case 'F8'              % 带约束的函数
        fobj = @F8;
        lb = [0,0,0];
        ub = [1,1,1];
        dim = 3;

    case 'F9'              % Branin函数
        fobj = @F6;
        lb = -5;
        ub = 20;
        dim = 2;

    case 'F10'             % Levy函数
        fobj = @F15;
        lb = -10;
        ub = 10;
        dim = 10;

    case 'F11'             % Rastrigin函数
        fobj = @F11;
        lb = -5.12;
        ub = 5.12;
        dim = 30;

    case 'F12'             % F4函数（最大绝对值）
        fobj = @F4;
        lb = -100;
        ub = 100;
        dim = 30;

    case 'F13'             % F1函数（Schwefel变种）
        fobj = @F1;
        lb = -50;
        ub = 50;
        dim = 10;

    case 'F14'             % F3函数（Shekel's Foxholes）
        fobj = @F3;
        lb = -65.536;
        ub = 65.536;
        dim = 2;

    case 'F15'             % Rosenbrock函数
        fobj = @F5;
        lb = -30;
        ub = 30;
        dim = 30;
        case 'F16'
        fobj = @F16;
        lb = -100;
        ub = 100;
        dim = 2;

    case 'F17'
        fobj = @F17;
        lb = -512;
        ub = 512;
        dim = 2;

    case 'F18'
        fobj = @F18;
        lb = -5.12;
        ub = 5.12;
        dim = 2;

    case 'F19'
        fobj = @F19;
        lb = -500;
        ub = 500;
        dim = 30;

    case 'F20'
        fobj = @F20;
        lb = 0;
        ub = pi;
        dim = 10;

end
end

%% === 测试函数定义区域 ===

function o = F1(x)  % F1: Schwefel-like 函数
    o = sum(-x .* sin(sqrt(abs(x))));
end

function o = F2(x)  % F2: 绝对值加乘积函数
    o = sum(abs(x)) + prod(abs(x));
end

function o = F3(x)  % F3: Shekel’s Foxholes
    aS = [...
    -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32;...
    -32 -32 -32 -32 -32 -16 -16 -16 -16 -16 0 0 0 0 0 16 16 16 16 16 32 32 32 32 32];
    for j = 1:25
        bS(j) = sum((x' - aS(:,j)).^6);
    end
    o = (1/500 + sum(1./([1:25] + bS))).^(-1);
end

function o = F4(x)  % F4: 取绝对值最大值
    o = max(abs(x));
end

function o = F5(x)  % F5: Rosenbrock函数
    dim = size(x,2);
    o = sum(100*(x(2:dim)-(x(1:dim-1).^2)).^2 + (x(1:dim-1)-1).^2);
end

function o = F6(x)  % F6: Branin函数
    o = (x(2) - (x(1)^2)*5.1/(4*pi^2) + 5/pi*x(1) - 6)^2 + 10*(1 - 1/(8*pi))*cos(x(1)) + 10;
end

function o = F7(x)  % F7: 带约束的罚函数
    o = sum(abs((x + 0.5)).^2);
    alpha = 10000;
    g1 = (x(1) + x(2)^2 - x(3) > 0) * (x(1) + x(2)^2 - x(3))^2 * alpha;
    g2 = (x(6)^3 + x(7)^2 + x(8)^3 > 0) * (x(6)^3 + x(7)^2 + x(8)^3)^2 * alpha;
    o = o + g1 + g2;
end

function o = F8(x)  % F8: 带约束的函数（不等式约束）
    o1 = -(x(1)^2 - x(2)^2 + x(2)*x(3));
    alpha = 10000;
    c(1) = 2*x(1) + x(2) + 3*x(3) - 6;
    c(2) = x(1)^2 + x(1)*x(2) + x(3)*x(2) - x(2) - 6;
    ceq = 0;
    o = o1 + alpha * sum((c > 0).*c.^2) + alpha * sum(ceq.^2);
end

function o = F9(x)  % F9: 带等式约束的函数
    o1 = -x(1) - 2*x(2) + 3*x(3);
    alpha = 10000;
    c(1) = -x(1) - x(2) + 3;
    c(2) = -x(3) - x(2) + 3;
    ceq(1) = x(1) + x(3) - 4;
    o = o1 + alpha * sum((c > 0).*c.^2) + alpha * sum(ceq.^2);
end

function o = F10(x)  % F10: Sphere函数
    o = sum(x.^2);
end

function o = F11(x)  % F11: Rastrigin函数
    o = sum(x.^2 - 10*cos(2*pi*x) + 10);
end

function o = F12(x)  % F12: Griewank函数
    o = sum(x.^2)/4000 - prod(cos(x./sqrt(1:length(x)))) + 1;
end

function o = F13(x)  % F13: Ackley函数
    o = -20*exp(-0.2*sqrt(mean(x.^2))) - exp(mean(cos(2*pi*x))) + 20 + exp(1);
end

function o = F14(x)  % F14: Zakharov函数
    o = sum(x.^2) + (sum(0.5*(1:length(x)).*x))^2 + (sum(0.5*(1:length(x)).*x))^4;
end

function o = F15(x)  % F15: Levy函数
    w = 1 + (x - 1)/4;
    o = sin(pi*w(1))^2 + sum((w(1:end-1)-1).^2 .* (1 + 10*sin(pi*w(1:end-1)+1).^2)) + ...
        (w(end)-1)^2 * (1 + sin(2*pi*w(end))^2);
end
% F16 - Schaffer Function N.2
function o = F16(x)
    o = 0.5 + (sin(x(1)^2 - x(2)^2)^2 - 0.5) / (1 + 0.001*(x(1)^2 + x(2)^2))^2;
end

% F17 - Eggholder Function
function o = F17(x)
    o = -(x(2)+47)*sin(sqrt(abs(x(2)+x(1)/2+47))) - x(1)*sin(sqrt(abs(x(1)-(x(2)+47))));
end

% F18 - Drop-Wave Function
function o = F18(x)
    r = sqrt(sum(x.^2));
    o = -(1 + cos(12*r)) / (0.5*r^2 + 2);
end

% F19 - Schwefel Function
function o = F19(x)
    o = 418.9829*length(x) - sum(x .* sin(sqrt(abs(x))));
end

% F20 - Michalewicz Function
function o = F20(x)
    m = 10;
    o = -sum(sin(x) .* (sin(((1:length(x)) .* x.^2) / pi)).^(2*m));
end

六、总结

本文整理了一套适用于群体智能优化算法的标准测试函数模块，支持 20 个经典函数的调用，涵盖了常见的单峰、多峰、约束、无约束函数，可用于算法开发、调试与对比实验。函数实现遵循标准格式，搭配 Get_Functions_details 接口，可便捷地集成进任何优化框架。

智能算法测试函数
12-03
这个测试函数，可以用来测试遗传算法，粒子群算法、模拟退火算法等智能算法
MATLAB 智能算法测试函数
09-05
MATLAB 智能算法常见测试函数公式 MATLAB实现
优化算法测试函数MATLAB代码完整版
07-22
优化算法测试函数MATLAB代码完整版，包含完整的MATLAB代码、数据及算法描述，都在这里了
智能算法经典测试函数
qq_44614115的博客
02-01 9947
本文总结了学习智能算法的过程中所了解到的经典测试函数
MATLAB优化算法测试函数
02-28
本来想自己改一些关于优化算法测试函数的MATLAB代码，但是后来发现网上是有这个代码的，所以来分享一下。
精选资源
帝企鹅EPO优化算法原理、测试函数及matlab代码
11-19
该算法结合了群体智能和自然选择机制，旨在解决复杂优化问题。在MATLAB环境中，EPO的实现通常包括以下几个关键步骤： 1. **初始化种群**：首先，随机生成一个初始的企鹅群体，每个企鹅代表一个解决方案，其位置和...
精选资源
标准粒子群算法优化测试函数shubert,matlab编程代码实现
11-21
在本文中，我们将深入探讨如何使用标准粒子群优化算法（PSO）来解决数学优化问题，特别是针对描述中的测试函数——Shubert函数。Shubert函数是一个多模态优化问题，具有多个全局最优解，这使得它成为检验优化算法...
精选资源
遗传算法优化粒子群算法求解shubert函数，ga-pso算法求解测试函数
06-02
在这个项目中，GA-PSO算法被应用来解决Shubert函数，这是一个经典的测试函数，因其多峰性和非线性特性而被广泛用于评估优化算法的性能。 Shubert函数是一个多峰函数，其表达式通常由一系列项组成，这些项与参数的...
粒子群优化算法（PSO ）源代码+23个经典测试函数
04-18
粒子群优化算法（PSO，Particle Swarm Optimization）是一种基于群体智能的优化算法，源自对鸟群和鱼群等动物集体行为的研究。PSO利用种群中的每个粒子在搜索空间中的移动来寻找最优解，粒子的位置和速度分别代表...
【智能优化算法-跳蛛优化算法】基于跳蛛优化算法求解单目标优化问题附matlab代码.zip
05-05
跳蛛优化算法是一种新兴的生物启发式全局优化方法，源于自然界中跳蛛高效寻找猎物的行为。这种算法在解决复杂的单目标优化问题时表现出色，能够有效地搜索全局最优解。在MATLAB环境中实现跳蛛优化算法，可以帮助研究...
群智能算法的标准测试函数
03-14
包含有Ronsenbrock，Schaffer，Schewel,Schwefel, ShiftedRonsenbrock, ShiftedSphere,Sphere,Step,SumDIfferent,SumSquares,Zakharov，等测试函数，代码是MATLAB实现的，并且都是子函数形式，方便使用，内有调用说明
Benchmark functions 优化算法测试函数
03-13
Benchmark functions.zip 是一些常用的优化算法测试函数，共有17个。
算法标准测试函数
12-24
Ackley，Alpine，Bohachevsky，Bohachevsky2，Goldstein_price，Griewank，Hyper_ellipsoid，Quadric_Noise，Rastrigrin，基于MATLAB实现，群智能算法实现
优化标准测试函数及MATLAB代码
04-29
目前常用的优化标准测试函数及MATLAB代码
智能优化算法常用测试函数
m0_49644580的博客
10-09 2434
智能算法测试函数
【matlab】智能优化算法——基准测试函数
m0_58683132的博客
07-01 2468
智能优化算法的基准测试函数是用于评估和优化算法性能的一组标准问题。这些测试函数模拟了真实世界优化问题的不同方面，包括局部最小值、全局最优解、高维度、非线性、不连续等复杂性。
智能优化算法：测试函数代码与图像分析
最新发布
weixin_42186387的博客
08-01 764
在研究和开发智能优化算法的过程中，测试函数发挥着至关重要的作用。测试函数，也被称作基准测试函数，是专为算法测试和性能评估设计的数学模型，它们模拟了优化问题中的目标函数。这些函数通常具有已知的全局最优解，使得研究人员可以验证算法的性能，比如收敛速度、解的质量、鲁棒性等。测试函数的主要作用包括：提供一个标准的比较基准：通过相同测试函数的性能评估，可以直接比较不同算法的优劣。帮助算法开发与调试：在算法开发阶段，测试函数能够及时反映算法改进带来的效果。预测算法在实际问题中的表现。
多种智能优化算法运行时间和不同函数测试对比附matlab代码
matlab_dingdang的博客
06-13 1253
智能优化算法是一种常用的求解最优化问题的方法，包括遗传算法、粒子群优化算法、蚁群算法等等。这些算法具有不同的优缺点和适用范围，因此在实际应用中需要进行对比。下面是一些常见的智能优化算法及其特点：遗传算法（GA）：通过模拟种群遗传过程来寻找最优解，具有全局搜索能力和收敛速度较快的特点。粒子群算法（PSO）：通过模拟粒子在解空间中的运动过程来寻找最优解，具有易于实现和求解速度快的特点。蚁群算法（ACO）：利用蚁群在食物与蚂蚁巢穴之间的搜索规律来寻找最优解，具有分布式搜索和适用于多目标优化等特点。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值