二叉树【通透理解】-面试必备-附代码

前言

本文通透的理解一下二叉树的特性，并且附上代码，方便读者进一步理解本文章讲解思路，如读者对本文内容有补充，欢迎发言

二叉树

一张图通透的告诉你三种遍历方法

下面笔者对下图进行一个说明，按照先序遍历的思想对二叉树进行遍历，可以得到1,2,4,4,4,2,5,5,5,2,1,3,6,6,6,3,7,7,7,3,1这种次序

• 如果我们要找先序遍历，在上述次序中每一个元素第一次出现的加入到先序遍历，比如4出现了三次，加入第一次，4后面还有一个2，但是前面已经加入了一个2，所以忽略;
• 如果我们要找中序遍历，在上述次序中每一个元素第二次出现的加入到中序遍历，比如4出现了三次，加入第二次，4前面还有一个2，是第一次出现的，所以忽略；
• 如果我们要找后序遍历，在上述次序中每一个元素第三次出现的加入到后序遍历，比如4出现了三次，加入第三次。5出现了三次，加入第三次，5后面有一个2，是第三次出现，加入到后序遍历；
  

好了，经过上面的讲解，相信大家对三种遍历方式已经有一种清晰的概念

三种遍历代码（递归）

不难看出，跟上面讲的内容一样，

• 先序遍历是在第一次遍历到节点输出head.value
• 中序遍历是在第二次遍历到节点输出head.value
• 后序遍历是在第三次遍历到节点输出head.value
  

三种遍历代码（非递归）

先序遍历

从栈里弹出就打印出元素

中序遍历

跟上面的不同在于，先遍历到左节点的根，之后在弹出，然后在遍历弹出节点的右节点，到null时弹出，周而复始

后序遍历

用到一个收集栈，每一个弹出的元素进入到收集栈，因为栈的后进先出原则，可以打到一个后序的目的

宽度优先遍历

从头结点开始，一行一行遍历，原理是准备一个队列，将头结点放进，然后先放左，后放右，因为队列的先进先出，所以达到了一行一行的输出

二叉树获取最大宽度

题目：求一个二叉树的最大宽度
这里需要开辟一个HashMap的空间，把每一层的宽度放进去

判断为搜索二叉树

搜索二叉树：左孩子小于父节点，父节点小于右节点

那么如何判断是否为搜索二叉树呢，主要是采用中序遍历来判断是否为升序数组，只不过在原本的中序遍历上输出的语句改为判断大小

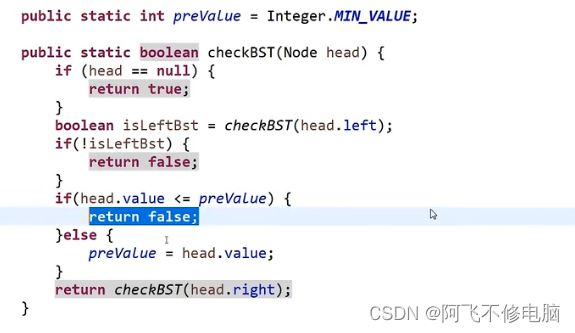
判断完全二叉树

完全二叉树：遍历二叉树，如果遇到一个节点只有左孩子没有右孩子，则以后的遍历到的节点都是叶子结点，则是完全二叉树

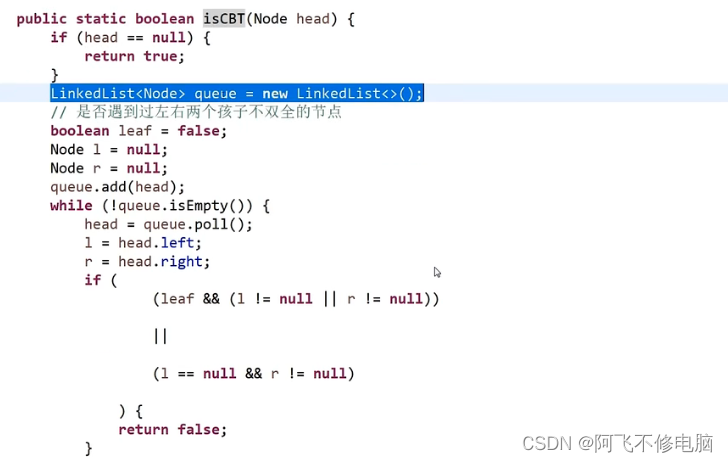
二叉树递归套路

目前有一个节点head，从head左边拿数据，再从head右边拿数据，然后跟当前节点的数据进行比较（相当于用了两个黑盒，然后你还能在该递归中将黑盒拆掉，这样递归才能连上）
比如说我们要求一个二叉树是否为搜索二叉树
我们需要从该节点拿到左孩子的数据，和右孩子的数据，即左树是否为搜索树，并且左树的max值（因为左树的max值要小于当前节点的值），右树同理，跟当前节点的value比较看是否满足题目条件

求满二叉树

如果一棵二叉树的高度为h，且它的节点数满足2^h^ - 1，满足满二叉树

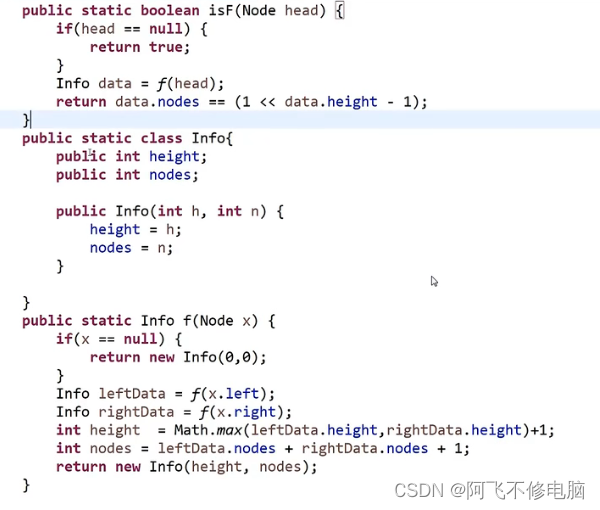
二叉树微软原题

可能刚看到这种题没有思路，但是你把纸条折一遍，并且在每个折痕上标上方向，会看到一种特殊的数据结构-二叉树