Pytorch_张量

qq_53398489

已于 2024-08-05 16:54:27 修改

阅读量976

点赞数 28

分类专栏： Pytorch_深度学习入门文章标签： pytorch 深度学习

于 2024-08-05 16:32:31 首次发布

本文链接：https://blog.youkuaiyun.com/qq_53398489/article/details/140857115

版权

Pytorch_深度学习入门专栏收录该内容

1 篇文章

订阅专栏

01 张量的数据类型

张量是一种数据结构，可以是一个矩阵或者是高维数组

1.1 张量的类型

创建浮点型数组时，默认数据类型是float32。创建整型数组时，默认数据类型是int 64

.dtype

获取张量的数据类型

1.2 类型的转化

张量类型的隐式转化

和NumPy中array相同，当张量各元素属于不同类型时，系统会自动进行隐式转化。

显式的转化方法—float() / double() / int()

02 张量的生成

2.1 torch.tensor() 函数

可以使用dtype参数指定张量的数据类型，requires_grad参数来指定张量是否需要进行梯度计算

下面针对张量A计算sum(A²)在每个元素上的梯度大小：

ndim、shape、size、numel

零维张量

在PyTorch中，还有一类特殊的张量，被称为零维张量。该类型张量只包含一个元素，但又不是单独一个数。

2.2 torch.Tensor() 函数

可以根据指定的形状生成张量

**_like

系列函数生成与指定张量维度相同的张量

2.3 利用Numpy数组生成张量

from_numpy

将Numpy数组转化成张量

.numpy()

将张量转化为Numpy数组

2.4 随机数生成张量

rand 、rand_like

randn、randn_like

2.5 其他生成张量的函数

arange
linspace

03 张量的操作

3.1 改变张量的形状

flatten

拉平，将任意维度张量转化为一维张量

reshape

unsqueeze

手动升维

注意理解维度和shape返回结果一一对应的关系，shape返回的序列有几个元素，张量就有多少维度。

squeeze

删除不必要的维度

3.2 获取张量中的元素

一、张量的符号索引

1. 一维张量索引

从左到右，从零开始

注：张量索引出来的结果还是零维张量，而不是单独的数。要转化成单独的数，需要使用item()方法。

冒号分隔，表示对某个区域进行索引，也就是所谓的切片

冒号前后没有值，表示索引整个区域

注：在张量的索引中，step位必须大于0

2. 二维张量索引

二维张量可以视为两个一维张量组合而成，而在实际的索引过程中，需要用逗号进行分隔，分别表示对哪个一维张量进行索引、以及具体的一维张量的索引。

3. 三维张量的索引

将三维张量视作矩阵组成的序列，则在实际索引过程中拥有三个维度，分别是索引矩阵、索引矩阵的行、索引矩阵的列。

3.3 拼接和拆分

一、view 方法

该方法会返回一个类似视图的结果，该结果和原张量对象共享一块数据存储空间，并且通过.view()方法，还可以改变对象结构，生成一个不同结构，但共享一个存储空间的张量。当然，共享一个存储空间，也就代表二者是“浅拷贝”的关系，修改其中一个，另一个也会同步进行更改。

“视图”的作用就是节省空间，而值得注意的是，在接下来介绍的很多切分张量的方法中，返回结果都是“视图”，而不是新生成一个对象。

二、张量的分片

1、分块：chunk函数

chunk函数能够按照某维度，对张量进行均匀切分，并且返回结果是原张量的视图。

注意：chunk返回结果是一个视图，不是新生成了一个对象

注：当原张量不能均分时，chunk不会报错，但会返回其他均分的结果

2、拆分：split函数

split既能进行均分，也能进行自定义切分。当然，需要注意的是，和chunk函数一样，split返回结果也是view。

均分情况

自定义切片

注: 当第二个参数位输入一个序列时，序列的各数值的和必须等于对应维度下形状分量的取值。例如，上述代码中，是按照第一个维度进行切分，而B总共有4行，因此序列的求和必须等于4，也就是1+3=4，而序列中每个分量的取值，则代表切块大小。

三、张量的合并操作

张量的合并操作类似于列表的追加元素，可以拼接、也可以堆叠。

拼接函数：cat

注意理解，拼接的本质是实现元素的堆积，也就是构成a、b两个二维张量的各一维张量的堆积，最终还是构成二维向量。

堆叠函数：stack

和拼接不同，堆叠不是将元素拆分重装，而是简单的将各参与堆叠的对象分装到一个更高维度的张量里。

注意对比二者区别，拼接之后维度不变，堆叠之后维度升高。拼接是把一个个元素单独提取出来之后再放到二维张量中，而堆叠则是直接将两个二维张量封装到一个三维张量中，因此，堆叠的要求更高，参与堆叠的张量必须形状完全相同。

04 张量计算

PyToch总共为Tensor设计了六大类数学运算，分别是：

1.逐点运算（Pointwise Ops）：指的是针对Tensor中每个元素执行的相同运算操作；
2.规约运算（Reduction Ops）：指的是对于某一张量进行操作得出某种总结值；
3.比较运算（Comparison Ops）：指的是对多个张量进行比较运算的相关方法；
4.谱运算（Spectral Ops）：指的是涉及信号处理傅里叶变化的操作；
5.BLAS和LAPACK运算：指的是基础线性代数程序集（Basic Linear Algeria Subprograms）和线性代数包（Linear Algeria Package）中定义的、主要用于线性代数科学计算的函数和方法；
6.其他运算（Other Ops）：其他未被归类的数学运算。

一、张量的广播（Broadcast）特性

在具体介绍张量的运算操作之前，我们先要了解张量的运算规则，其中最重要的一点，就是张量具备和NumPy相同的广播特性，也就是允许不同形状的张量之间进行计算。

1、相同形状的张量计算

相同形状数组总是可以进行广播计算。尽管是对应位置元素进行计算，但本质上也是应用到了广播特性。

2、不同形状的张量计算

广播的特性是在不同形状的张量进行计算时，一个或多个张量通过隐式转化，转化成相同形状的两个张量，从而完成计算的特性。但并非任何两个不同形状的张量都可以通过广播特性进行计算，因此，我们需要了解广播的基本规则及其核心依据。

2.1 标量和任意形状的张量

标量可以和任意形状的张量进行计算，计算过程就是标量和张量的每一个元素进行计算。

2.2 相同维度、不同形状的张量之间计算

对于返回结果，我们可以看成是一个序列，代表着张量各维度的信息。对于二维张量，由于我们可以将其视作一个矩阵，可以说t2是一个拥有三行四列的二维张量，但这种理解方式对于更高维度张量就存在一定的局限，因此我们需要树立另外一种理解方法，那就是：t2是由3个一维张量组成，并且该一维张量、每个都包含四个元素。

t2是由3个二维张量组成了三维张量，并且每个二维张量，都是由四个一维张量组成，每个一维张量又包含5个。

接下来，来探讨相同维度、不同形状的张量之间的广播规则。

二维张量的广播

t31的形状是（1， 4），和t3的形状（3， 4）在第一个分量上取值不同，但该分量上t31取值为1，因此可以广播，也就可以进行计算

注意理解：此处的广播相当于将t31的形状（1， 4）拓展成了t3的（3， 4），也就是复制了第一行三次，然后二者进行相加。当然，也可以理解成t31的第一行和t3的三行分别进行了相加。

t3和t32实际计算过程如下：

若t3和t33的形状第一个分量维度不同，但二者取值均不为1，则无法广播

此时，t34的形状是（3， 1），而t35的形状是（1， 3），二者的形状在两个份量上均不相同，但都有存在1的情况，因此也是可以广播的

三维张量的广播

只有一个分量不同，并且该分量为1

两个张量的形状上有两个分量不同时，只要不同的分量仍然有一个取值为1，则仍然可以广播

广播过程：

2.3 不同维度的张量计算过程中的广播

对于不同维度的张量，我们首先可以将低维的张量升维，然后依据相同维度不同形状的张量广播规则进行广播。而低维向量的升维也非常简单，只需将更高维度方向的形状填充为1即可，例如：

转化之后表示只包含一个二维张量的三维张量，且二维张量就是t2

转化之后表示只包含一个三维张量的四维张量，且三维张量只包含一个二维张量，且二维张量就是t2

t3和t2的计算过程，就相当于形状为（1，2，2）和（3，2，2）的两个张量进行计算

二、逐点运算（Pointwise Ops）

针对Tensor中每个元素都进行的数学科学运算，逐点运算主要包括数学基本运算、数值调整运算和数据科学运算三块，相关函数如下：

1、Tensor基本数学运算

2、Tensor数值调整函数

注：虽然此类型函数是数值调整函数，但并不会对原对象进行调整，而是输出新的结果。

而若要对原对象本身进行修改，则可考虑使用`方法_()`的表达形式，对对象本身进行修改。此时方法就是上述同名函数。

3、Tensor常用科学计算

tensor的大多数科学计算只能作用于tensor对象

tensor的大多数科学运算具有一定的静态性

所谓静态性，指的是对输入的张量类型有明确的要求，例如部分函数只能输入浮点型张量，而不能输入整型张量。

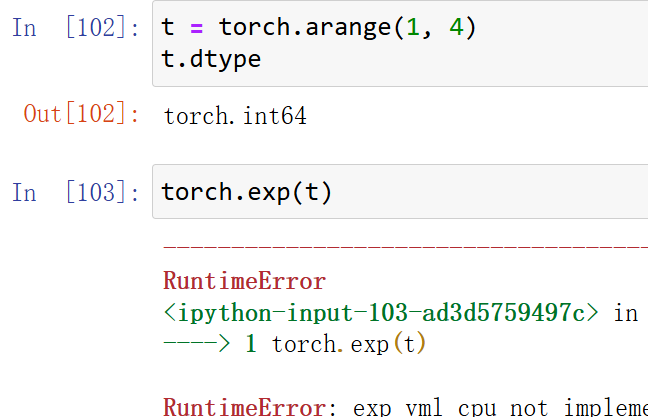
在PyTorch中，由于会涉及GPU计算，因此很多时候元素类型不会在实际执行函数计算时进行调整。此处的科学运算大多数都要求对象类型是浮点型，我们需要提前进行类型转化。

4、排序运算：sort

在PyTorch中，sort排序函数将同时返回排序结果和对应的索引值的排列。

三、规约运算

规约运算指的是针对某张量进行某种总结，最后得出一个具体总结值的函数。此类函数主要包含了数据科学领域内的诸多统计分析函数，如均值、极值、方差、中位数函数等等。

1、Tensor统计分析函数

2、dist计算距离

dist函数可计算闵式距离（闵可夫斯基距离），通过输入不同的p值，可以计算多种类型的距离，如欧式距离、街道距离等。闵可夫斯基距离公式如下：

p取值为2时，计算欧式距离

p取值为1时，计算街道距离

3、规约运算的维度

由于规约运算是一个序列返回一个结果，因此若是针对高维张量，则可指定某维度进行计算。

4、二维张量的排序

和上述过程类似，在进行排序过程中，二维张量也可以按行或者按列进行排序

四、比较运算

比较运算是一类较为简单的运算类型，和Python的布尔运算类似，常用于不同张量之间的逻辑运算，最终返回逻辑运算结果（逻辑类型张量）。基本比较运算函数如下所示：

五、BLAS和LAPACK运算

1、BLAS和LAPACK概览

BLAS（Basic Linear Algeria Subprograms）和LAPACK（Linear Algeria Package）模块提供了完整的线性代数基本方法，由于涉及到函数种类较多，因此此处对其进行简单分类，具体包括：

矩阵的形变及特殊矩阵的构造方法：包括矩阵的转置、对角矩阵的创建、单位矩阵的创建、上/下三角矩阵的创建等；
矩阵的基本运算：包括矩阵乘法、向量内积、矩阵和向量的乘法等，当然，此处还包含了高维张量的基本运算，将着重探讨矩阵的基本运算拓展至三维张量中的基本方法；
矩阵的线性代数运算：包括矩阵的迹、矩阵的秩、逆矩阵的求解、伴随矩阵和广义逆矩阵等；
矩阵分解运算：特征分解、奇异值分解和SVD分解等。

2、矩阵的形变及特殊矩阵构造方法

矩阵的形变方法其实也就是二维张量的形变方法。另外，在实际线性代数运算过程中，经常涉及一些特殊矩阵，如单位矩阵、对角矩阵等，相关创建方法如下：

Tensor矩阵运算：

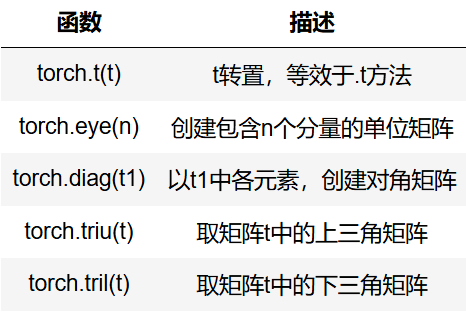
转置

对角矩阵

三角矩阵

3、矩阵的基本运算

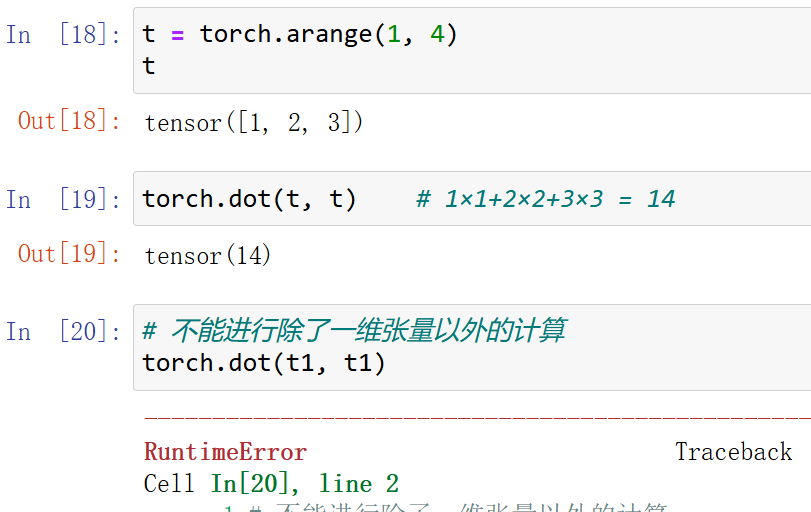
dot\vdot：点积计算

注意，在PyTorch中，dot和vdot只能作用于一维张量，且对于数值型对象，二者计算结果并没有区别，两种函数只在进行复数运算时会有区别。

mm：矩阵乘法

mv：矩阵和向量相乘

PyTorch中提供了一类非常特殊的矩阵和向量相乘的函数，矩阵和向量相乘的过程我们可以看成是先将向量转化为列向量然后再相乘。

在实际执行向量和矩阵相乘的过程中，需要矩阵的列数和向量的元素个数相同

bmm：批量矩阵相乘

所谓批量矩阵相乘，指的是三维张量的矩阵乘法。我们知道，三维张量就是一个包含了多个相同形状的矩阵的集合。例如，一个（3， 2， 2）的张量，本质上就是一个包含了3个2*2矩阵的张量。而三维张量的矩阵相乘，则是三维张量内部各对应位置的矩阵相乘。由于张量的运算往往涉及二维及以上，因此批量矩阵相乘也有非常多的应用场景。