计算机组成原理第二章：数据的表示与运算

数制与编码

其中编码和校验码部分已经在考纲内删除了，可不用再关心。

数据的表示

二进制：

十六进制：

由此可推广一般化：

进制转换：

二进制转化为额其他进制：
二进制转化为八进制，每三个位看做一组，然后进行计算，不够三的倍数时添加0即可，二进制转十六进制同理。每四个看做一组即可。

十进制转化为其他进制：
整数部分：
小数部分：

快捷方法：

以上图的112.25为例，128肯定就大于了，不行，所以只能用64，然后112.25-64剩余58.25，不够64所以用32，以此类推，小数点部分一样的道理，没用到的地方就用0表示，用到的地方就用1表示，就能拿到二进制数值了。

真值和机器数

定点数的表示和运算

定点数的表示

无符号数

不会变少，如上图所示，一位拿来做符号位的话，那么我们只能表示2的7次方-1个数据，正数能表示这么多，负数也能表示这么多，那么合起来不就又是2的8次方-1吗，所以能表示的数据量并不会减少。另外还要注意，计算机的位数其实就是指的机器字长。

主要就是用于表示计算机内部的一些非负数值。

有符号数

有符号数定点表示（原码）

定点整数

定点小数

有符号数的定点表示（反码）

有符号数的定点表示（补码）

上面的规定中，假设的是机器字长为八位，所以补码整数表示为了-2的7次方，但是如果机器字长为n位的话，就应该是-2的n次方，而补码小数则永远都是-1，没有区别。

有符号数的定点表示（移码）

为什么移码只有整数？因为之前介绍补码的时候已经说过了，不管机器字长多少，补码小数的表示范围为-1到1-2的-n次方,而-1已经由1.00000表示了，同时移码又是建立在补码基础上的，就是将补码的符号位取反，那么唯一的一个负数-1都被取反变成正1了，所以显而易见，移码则只能表示整数了。

总结

定点数的运算

移位运算（算数移位最常考）

算术移位（原码）

丢失精度什么意思？比如上图中提到的，当我们将9继续算数右移一位，可以看见低位移出去了一个1，这就意味着9又除以了2，现实生活中应该等于4.5，但是因为丢弃未不等于0，丢失了0.5的精度就变成了4。

出现严重错误怎么理解？上图中真值为72当它继续左移时，会发现高位的1会被丢弃（因为已经超过了机器字长所能表示的最大位数），所以计算剩余的值为16，被丢弃的1的权重应该为2的7次方即128，然后再加上现在还剩的16为144，这才是我们正好应该72*2所得到的值，但因为1被丢弃了所以只剩16了，即严重的精度缺失。

算数移位（反码）

负数反码的移位运算高低位补1是因为反码是由原码符号位不动数值位按位取反得来的，所以在负数反码高低位补的1就是原来原码上的0。

算数移位（补码）

总结

逻辑移位（最简单的一种）

循环移位

带进位循环移位：

移位过后如下：
就相当于走了一个循环，右移就是最右边的数值位移到CF里面，然后CF里面的值再填充到字长里面即可，左移同理。

不带进位循环移位：
注意：移动位就是指字长里面需要被移出的那个数值就叫移动位。

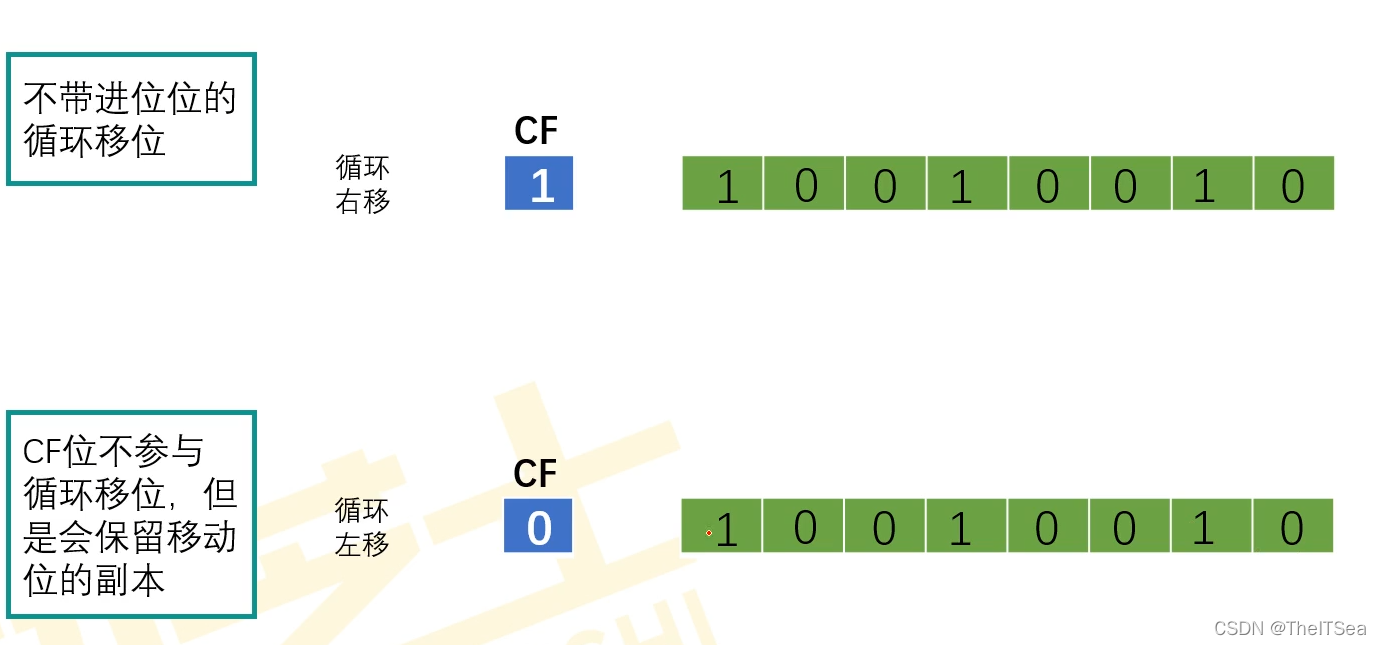
大概过程是：
先不看CF位，字长里面先进行一次循环移位，然后CF位再记录下来移动位的那个数值即可：

总结一下：

加减法运算

原码加减法

加法器直接对原码进行计算可能会出错：

所以需要采取一定的规则：

即：

之前的错误例子改正后即：

补码加减法

对于补码来说，无论加法还是减法最后都会转化为加法，由加法器实现运算，符号位也参与运算。

移码加减法（不考，了解即可）

溢出判断

1）符号比较法

2）双进位法

可以发现上述中的例子左边部分为上溢出，右边部分没有溢出。

3）双符号位法

符号拓展

乘除法运算（难，考的不多）

原码一位乘

两个数一正一负，按照概念中说的，我们始终将MQ中的乘数看成正数来计算，在最后得出结果时再来进行正负的判断。
由上图可知，乘数最低位为1，我们将部分积加上我们的被乘数，得到01101存入我们的ACC寄存器中：

然后接下来采用类似的操作，但是乘数最低位因为已经用过了，所以进行逻辑右移，ACC的符号位不动，最高位顺下右移补0，所以最低位的值就右移至MQ的高位，而MQ的低位就被抛弃了。然后再进行重复的加操作，ACC+X：

再进行逻辑右移，可以发现此时MQ寄存器中的最低位为0，所以让ACC寄存器+0即可：

接下来都是如法炮制，因为乘数4位。所以进行4次操作之后就已经拿到结果了：

最后ACC中的内容就是最终结果的高位，MQ中的内容就是最终结果的低位：

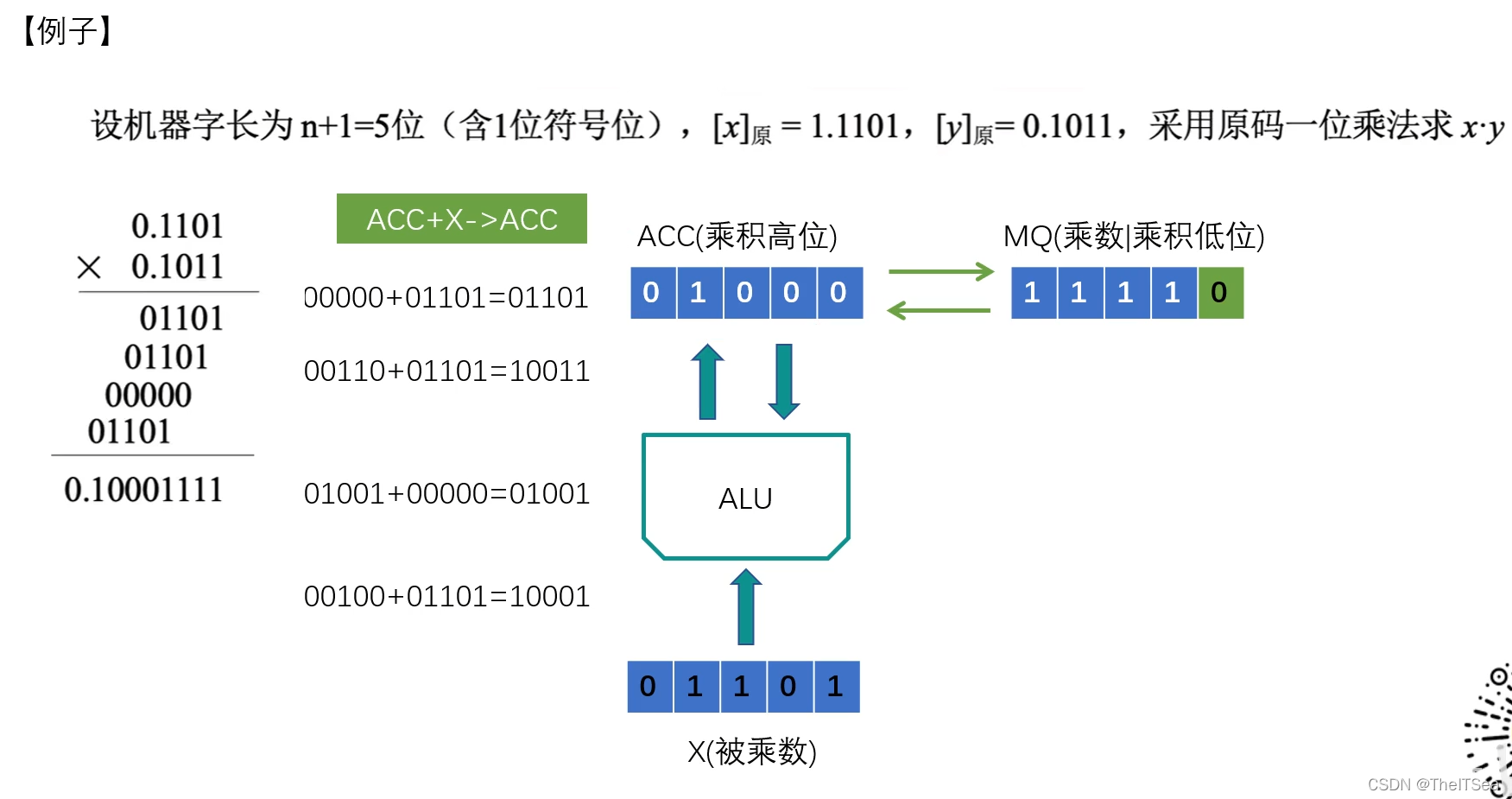
最后结果的符号单独处理：

在试卷上用下面的方法更方便：

补码一位乘

原码一位除（考的少）

计算机中怎么实现这个过程呢？有两种方式：一是恢复余数法，二是加减交替法，这里先讲第一种：

恢复余数法

同样是需要ACC、MQ寄存器和ALU处理器来实现：

在我们手动计算中，我们自己会认为01011比01101小，所以会先补一个0，但是计算机不知道，所以计算机在进行运算时第一次上商一定是先上1，上1了之后再进行一个判断：

现在计算机知道了01011+10011的结果（作减法的结果）是小于0的，是负数，那么接下来肯定就不能进行运算了，所以现在我们又恢复这个除数，并且把第一次上商的1改成0，ACC里面的被除数也恢复回01011：

然后我们对ACC和MQ进行左移，这样ACC的最高位0就被丢弃了，然后ACC内容变成10110，对于MQ也要左移，但是记得在每次进行除法前我们都要先让计算机默认商1，当商1的结果为正数时，才能继续正常除法。

可以看到这一次的结果是个正值，那么说明我们刚刚的商1是正确的，所以我们更新ACC里的值为01001，MQ里面的商1的值也保留。现在我们又将ACC和MQ左移一位：

然后过程类似，又是先通过默认商1来判断是否能够继续进行，能则留下该商1然后更新ACC，左移继续操作；不能则继续左移即可。

重复这个操作直到最后，得到答案：

加减交替法

补码一位除（和原码一位除差不多）

浮点数的表示和运算

一般浮点数的表示

IEEE 754标准

浮点数运算

浮点数加减运算

浮点数乘除法（考纲未要求，了解就好）

加餐内容（感兴趣可以看看，关于硬件的东西）