计算机组成原理第二章：数据的表示和运算

江上舟摇li

已于 2025-04-06 22:06:42 修改

阅读量743

点赞数 30

分类专栏：计算组组成原理文章标签：硬件工程

于 2025-04-06 22:04:27 首次发布

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.youkuaiyun.com/m0_59571950/article/details/147029300

版权

计算组组成原理专栏收录该内容

2 篇文章

订阅专栏

一.数制与编码

1.1进制转换

二进制转8进制和16进制：分别3位，4位一组，拆开组数

反过来8进制和16进制转二进制也是拆开数字转换

十进制小数转二进制

并不是每个十进制小数都能用二进制小数表述，但任意一个二进制小数都可以用十进制小数表述

整数部分正常转

小数部分乘基取整，乘积为1.0时结束

比如123.6875

1.2定点码的编码表示

原码：表示浮点数的尾数

取值范围：

源码整数： $-(2^n-1)<=x<=2^n-1$

原码小数： $-(1-2^{-n})<=x<=1-2^{-n}$

反码：

若符号位为0，则反码=原码

若符号位为1，则将除符号位以外的数值位全部取反

原码和反码的0不唯一，即存在+0和-0

补码：表示整数

若符号位为0，则补码=原码

若符号位为1，则补码=反码末位+1=原码除除符号位以外的数值位全部取反，末位+1

表示范围：

补码整数： $-2^n<=x<=2^n-1$

补码小数： $-1<=x<=1-2^{-n}$

tip:[x]补快速求[-x]补的办法

符号位，数值位都取反，末位+1

移码：浮点数的阶码,只能表示整数

在补码的基础上对符号位取反

表示范围

$-2^n<=x<=2^n-1$

真值=移码-偏置值。

表示范围

移码整数： $-2^n<=x<=2^n-1$

补码和移码的0是唯一的。

1.3整数的表示

无符号数，有符号数

c语言的整数类型和状态转换：

有符号数转无符号数：转为补码，符号位加入数值运算，之后去掉符号

强制类型转换的结果是保持二进制各位不变，仅改变解释这些位的方式（不改变内容，仅改变解释方式）

无符号数转有符号数：原码转为补码

eg：65535= $2^{16}-1$ =1111 1111 1111 1111 $\Rightarrow$ （补码）1,000 0000 0000 0001=-1

长字转为短字：高位截断，低位保留：

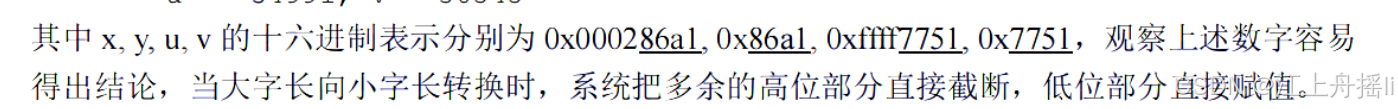
短字转为长字：符号扩展

1.3习题小节

对于13题，可以这么想：[x]补=1,x1x2x3x4x5x6-> $x6*2^0+x5*2^1+x4*2*2+....x1*2^5+1*(-2^6)=sum-64$

23:补码1000 0000，移码=0000 0000

24：真值=移码-偏置（作为无符号数运算），A真值=0011 1111-127=-64

25：[B]补=（全部取反，末位+1）[-B]补

二.运算方法和运算电路

2.1基本运算部件

运算器：ALU（核心部件是加法器）,移位器，状态寄存器（PSW），通用寄存器

带标志加法器：

几个标志：

OF，判断有符号数加减运算是否溢出，OF=最高进位 xor 次高进位，0没溢出，1溢出

SF,判断有符号数加减运算的正负性，0为正，1为负，SF=最高位本位和

ZF，判断加减运算结构是否为0，0不为0，1为0

CF，判断无符号数加减运算是否溢出，CF=最高进位 xor sub(若为减法，sub=1,若为加法,sub=0)

的

eg:有符号数8bit补码1000 0000(-128)+1111 1111(-1)

OF=1 xor 0 =1

SF=0(正)

ZF=0

若为无符号：CF=1 XOR 0 = 1

判断溢出也可以通过化为常数运算，下面是常数运算溢出的情况：

正+正=负

负+负=正

负-正=正

正-负=负

算数逻辑单元ALU：

是一种组合逻辑电路，包括算数运算和逻辑运算，加减乘除都可以归结为加法运算，因此其核心为带标志加法器，ALUop位数决定了操作种类：比如位数为3，最多有8种操作，同时ALU也可以实现左移和右移操作

2.2定点数的移位运算

逻辑移位：将操作数视为无符号整数，左移高位移除，低位补0；右移低位移除，高位补0

算数移位：将操作数视为有符号整数（补码，算数运算）

左移高位移除，低位补0，若左移前后符号位不一致，则溢出

右移低位移除，高位补符号位，若低位1移除，则影响精度

eg:0111 0100 << 1110 1000

eg:0011 0001 >> 0001 1000(影响精度）

2.3定点数的加减运算

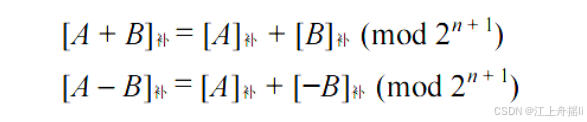
加减运算电路：

这里低位进位同sub位一致

2.4定点数的乘除运算

看视频

2.5习题小节

地址寄存器不属于运算器，而属于存储器

11：若老实算CD难搞，可以转换为真值，8位补码范围: $-2^7<=x<=2^7-1$

12:存储模4仅需要一个符号位

34:有符号->补码，无符号->无符号

32777 = 0000 0000 0000 0000 1000 0000 0000 1001（原码）

32777 = 0000 0000 0000 0000 1000 0000 0000 1001（补码）

截高留低si=1000 0000 0000 1001

j=1111 1111 1111 1111 1000 0000 0000 1001

三.浮点数的表示和运算

3.1浮点数的表示

公式：真值=阶码-偏置（按无符号数）

例：1010 1111(阶码） 0110 0100 0000 0000 0000 0000

真=阶-偏=1+2+4+8+32-64=-17 $\Rightarrow$ -0.0110 0100（尾数） $*2^{-17}$

浮点数的表述范围：

运算结果大于最大正数时称为正上溢，小于绝对值最大负数时称为负上溢，正上溢和负上溢
统称上溢。数据一旦产生上溢，计算机必须中断运算操作，进行溢出处理。当运算结果在0至最
小正数之间时称为正下溢，在0至绝对值最小负数之间时称为负下溢，正下溢和负下溢统称下溢。
数据下溢时，浮点数值趋于零，计算机将其当作机器零处理。

浮点数的规格化：尽可能保留有效数字的位数

基数为2的原码规格化尾数M应满足1/2<|M<1，形式如下：①正数为0.1×..×的形式，最
大值为0.11...1，最小值为0.100..0，表示范围为 $1/2<M<(1-2^{n})$ ;②负数为1.1×...×的形式，最
大值为1.10...0，最小值为1.11..1，表示范围为 $-(1-2^{-n})<=M<=-1/2$ 。

IEEE754标准：

8位阶码的真值范围是-126~127

这里需要记住的是他们的十进制的偏置值

IEEE规定有一个隐藏位1，因此23位尾数的实际表示24位有效数字，并且隐藏位1在小数点之前，比如 $(12)_{10}=(1100)_{2}$ ,规格化为 $1.1*2^3$

在这里，偏置值并不是通常的n位移码 $2^{n-1}$ ,而是 $2^{n-1}-1$ ,因此其偏置分别位127和1023

3.2浮点数的加减运算

对阶：使两个操作数的小数点位置对齐，即两个数阶码相等，采用小阶码向大阶码对齐的原则，将小阶码的尾数右移一位（基数位2），阶码+1，直到两者阶码相等。为保证运算的精度，尾数右移，低位移除的位不要丢掉，应该保留并参与尾数部分的运算。

尾数加减：因为IEEE 754浮点数尾数有隐藏位，因此进行尾数加减时，必须将隐藏位还原到尾数部分，运算后的尾数不一定是规格化的

尾数规格化：

IEEE754 的标准是保证小数点左边为1。

普通浮点数的规格化是：

对原码尾数：

正0.1xxxxxxx,最大：0.11111.....1,最小:0.100000...0000；

负1.1xxxxxxx,最大1.10000.....0,最小1.111111.1111

对补码尾数的规格化是：

正0.1xxxxxxx,最大0.1111.111111,最小0.1000000.0000

负1.0xxxxxxxx，最大1.011111.1111,最小1.0000000.0000

舍入：在对阶和尾数右规时候存在舍入

判断溢出：看阶码是否上溢

若一个正指数超过了最大允许值(127或1023），发生指数上溢，产生异常；

若一个负指数超过了最小允许值(-149或-1047），发生指数下溢，把结果按机器0处理；

3.3 C语言的浮点数类型

隐式类型转换：

int->float:不会溢出，但当int转换为浮点数的尾数的有效位大于24时，需要舍入处理，影响精度

int或float->double:可以精确保留

double->float：可能溢出

float或double->int:数据会向0方向截断（仅保留整数部分），并且大数转换会发生溢出

3.4数据的大小端和对齐方式：

大端对齐：数据低位放在地址高位

小端对齐：数据低位放在地址低位

按边界对齐：假设字长为32位（机器字长），按边界对齐要求其存储地址是自身大小的整数倍，半字地址一定是2的整数倍，字地址一定是4的整数倍，可以提高存取数据的速度

3.5习题小节：

3：基数大，范围大，精度低

7：eg $11.01100*2^4\Rightarrow 1.10110*2^5$ ,阶数增大，尾数右移，负数高位补0，右移低位补0

阶码减小，尾数左移，但对阶一定是小阶码向大阶码对齐

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。