- 回溯算法是在一棵树上的 深度优先遍历(因为要找所有的解,所以需要遍历);
在 Java 中,当你使用 List<List<Integer>> res = new ArrayList<>() 这样的语句时,右侧的 new ArrayList<>() 实际上利用了 Java 的类型推断功能,这是 Java 7 引入的钻石操作符 (<>) 的特性。这里解释一下为什么不需要在右侧声明两层列表结构。
类型推断和钻石操作符
-
类型推断:Java 编译器可以从左侧的变量声明中推断出右侧的泛型类型。当你声明
List<List<Integer>>时,编译器知道你需要的是一个ArrayList,其元素类型为List<Integer>。 -
钻石操作符 (
<>):Java 7 引入的这个特性允许你在创建泛型实例时不必重复泛型类型。你只需要在左侧声明完整的泛型类型,然后在右侧使用空的钻石操作符。编译器会自动填充正确的泛型类型。
理解列表嵌套
-
外层列表:在
List<List<Integer>>中,外层的List是容器,它将包含一些元素,这些元素本身也是列表。 -
内层列表:内层的
List<Integer>表示这些元素是整数列表。这些内层列表需要单独创建并添加到外层列表中。
实例创建
当你写 new ArrayList<>() 时,你实际上只是创建了外层的 ArrayList 实例,内层的 List<Integer> 实例需要在后续的操作中单独创建并添加。例如:
List<List<Integer>> res = new ArrayList<>();
List<Integer> innerList = new ArrayList<>();
innerList.add(1); // 添加一些整数到内层列表
res.add(innerList); // 将内层列表添加到外层列表
- temp的大小判定在每次进入下一层时也就是刚刚进入travelsal时操作,且因为temp是全局变量,所以要new一个新的。
- 下一层travelsal中应添加i+1而不是start+1

class Solution {
List<Integer> temp=new LinkedList<>();
List<List<Integer>> result=new LinkedList<>();
public List<List<Integer>> combine(int n, int k) {
travelsal(1,n,k);
return result;
}
public void travelsal(int start,int n,int k)
{
if(temp.size()==k)
{
result.add(new LinkedList<>(temp));
return;
}
for(int i=start;i<=n;i++)
{
System.out.println(i);
temp.add(i);
travelsal(i+1,n,k);
temp.removeLast();
}
}
}本题可以进行剪枝
如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了,那么就没有必要搜索了。
还需要元素个数:k-temp.size() 目前可选元素个数:n-i+1(左闭右闭)
因此不等式 n-i+1>=k-temp.size()
i<=temp.size()+n+1-k
class Solution {
List<List<Integer>> result=new ArrayList<>();
List<Integer> temp=new ArrayList<>();
public List<List<Integer>> combine(int n, int k) {
backtracking(1,n,k);
return result;
}
public void backtracking(int start,int n,int k)
{
if(temp.size()==k)
{
//深度到达k
result.add(new ArrayList<>(temp));
return;
}
//未到达k
for(int i=start;i<=n+temp.size()+1-k;i++)
{
temp.add(i);
backtracking(i+1,n,k);
//到这里的时候已经添加完一个temp了
temp.remove(temp.size()-1);
}
return;
}
}class Solution {
List<List<Integer>> result=new ArrayList<>();
List<Integer> temp=new ArrayList<>();
public List<List<Integer>> combinationSum3(int k, int n) {
backtracking(1,k,n);
return result;
}
public void backtracking(int start,int k,int n)
{
//k是深度 9是宽度 n是还差多少到目标值
if(temp.size()==k&&n==0)
{
result.add(new ArrayList<>(temp));//因为java中是引用,所以要new一个新的
return;
}
if(n<=0){
//k不满足要求
return;}
if(temp.size()==k)
{
//没达到要求的n
}
for(int i=start;i<=10-k+temp.size();i++)
{ //剪枝不等式:k-tmp.size<=9-i+1
// i<=10-k+tmp.size()
n-=i;
temp.add(i);
backtracking(i+1,k,n);
n+=i;
temp.removeLast();
}
return;
}}class Solution {
List<String> result=new ArrayList<>();
StringBuilder temp=new StringBuilder();
public List<String> letterCombinations(String digits) {
//digits是数字串 164
if(digits==null||digits.length()==0) return result;
String[] numString={"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
backtracking(digits,numString,0);
return result;
}
public void backtracking(String digits,String[] numString,int num)
{
//nums是深度 与digits.length()比较 用于遍历深度
if(num==digits.length())
{
result.add(temp.toString());
return;
}
//取出numstring中digtis[num]对应的字符串 abc
String str=numString[digits.charAt(num)-'0'];
for(int i=0;i<str.length();i++)
{
temp.append(str.charAt(i));
backtracking(digits,numString,num+1);
temp.deleteCharAt(temp.length() - 1);
}
return;
}
}
startindex的作用是实现树同层剪枝 ,树枝不剪枝。而本题深度不做限制,条件是数组中的最小值大于target,或者也可以写一个sum来记录
class Solution {
public List<List<Integer>> result=new ArrayList<>();
public List<Integer> temp=new ArrayList<>();
int min=Integer.MAX_VALUE;
public List<List<Integer>> combinationSum(int[] candidates, int target) {
for(int i=0;i<candidates.length;i++)
{
if(candidates[i]<min)
{
min=candidates[i];
}
}
backtracking(candidates,target,0);
return result;
}
public void backtracking(int[] candidates,int target,int startindex)
{
//满足条件
if(target==0)
{
result.add(new ArrayList<>(temp));
return;
}
if(min>target)
{
//查找失败 最小的都大于剩下的目标值
return;
}
// if()
for(int i=startindex;i<candidates.length;i++)
{
target-=candidates[i];
temp.add(candidates[i]);
backtracking(candidates,target,i);//向更深处遍历可选i 但是横向遍历时会变成i+1 满足了树层剪枝
target+=candidates[i];
temp.removeLast();
}
return;
}
}
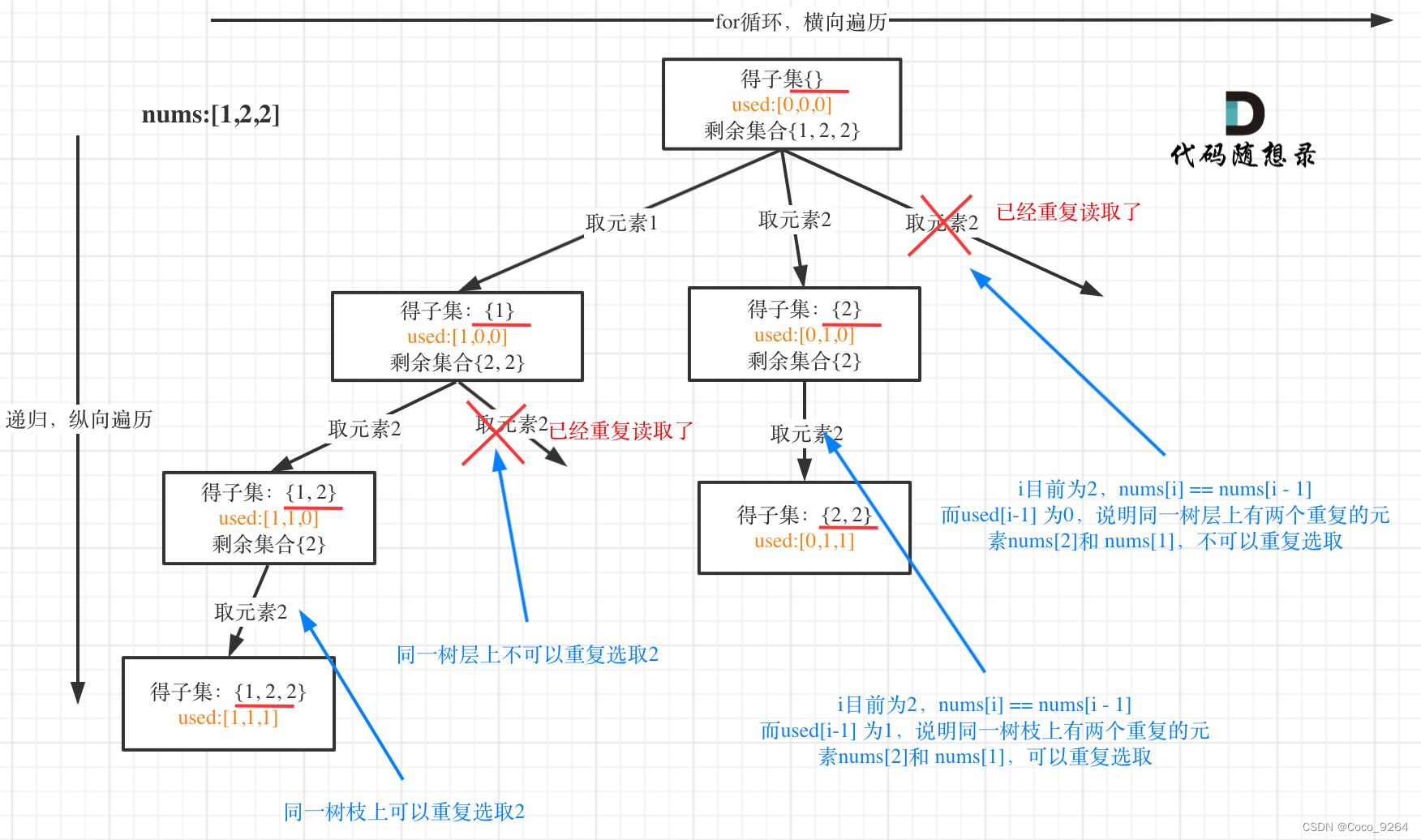
- used[i - 1] == true,说明同一树枝candidates[i - 1]使用过
- used[i - 1] == false,说明同一树层candidates[i - 1]使用过
为什么 used[i - 1] == false 就是同一树层呢,因为同一树层,used[i - 1] == false 才能表示,当前取的 candidates[i] 是从 candidates[i - 1] 回溯而来的。
而 used[i - 1] == true,说明是进入下一层递归,去下一个数,所以是树枝上,如图所示:
这里我们这里直接用startIndex来去重也是可以的, 就不用used数组了。
class Solution {
public List<List<Integer>> result=new ArrayList<>();
public List<Integer> temp=new ArrayList<>();
int min=Integer.MAX_VALUE;
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
if(candidates==null||candidates.length==0) return result;
Arrays.sort(candidates); // 对数组进行排序
for(int i=0;i<candidates.length;i++)
{
if(candidates[i]<min)
{
min=candidates[i];
}
}
backtracking(candidates,target,0);
return result;
}
public void backtracking(int[] candidates,int target,int startindex)
{
//满足条件
if(target==0)
{
result.add(new ArrayList<>(temp));
return;
}
if(min>target)
{
//查找失败 最小的都大于剩下的目标值
return;
}
// if()
for(int i=startindex;i<candidates.length;i++)
{
if (i > startindex && candidates[i] == candidates[i - 1]) {
continue;
}
target-=candidates[i];
temp.add(candidates[i]);
backtracking(candidates,target,i+1);//向更深处遍历
target+=candidates[i];
temp.removeLast();
}
return;
}
}用HashSet: 不用clear是因为我们在backtraking里每进入一次都声明一个新的set,因此同一个set只能限定一个backtracking里的同层相同元素
class Solution {
List<List<Integer>> result = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
Arrays.sort( candidates );
if( candidates[0] > target ) return result;
backtracking(candidates,target,0,0);
return result;
}
public void backtracking(int[] candidates,int target,int sum,int startIndex){
if( sum > target )return;
if( sum == target ){
result.add( new ArrayList<>(path) );
}
HashSet<Integer> hashSet = new HashSet<>();
for( int i = startIndex; i < candidates.length; i++){
if( hashSet.contains(candidates[i]) ){
continue;
}
hashSet.add(candidates[i]);
path.add(candidates[i]);
sum += candidates[i];
backtracking(candidates,target,sum,i+1);
path.removeLast();
sum -= candidates[i];
}
}
}class Solution {
List<String> temp=new ArrayList<>();
List<List<String>> result=new ArrayList<>();
// Deque<String> deque = new LinkedList<>();
public List<List<String>> partition(String s) {
if(s==null||s.length()==0) return result;
backTracking(s,0);
return result;
}
private void backTracking(String s,int startIndex)
{
if(startIndex >=s.length()){
//分割竖现超过了s的长度
result.add(new ArrayList<>(temp));
return;
}
for(int i=startIndex;i<s.length();i++)
{
//i=startindex就是处理竖线后的字符串
if(isH(s,startIndex,i))
{
//提取字符串 左闭右开
String str=s.substring(startIndex,i+1);
temp.add(str);
}else{
continue;
//不是回文串就不向下深度延伸了
}
backTracking(s,i+1);
temp.removeLast();
}
}
private boolean isH(String s,int startIndex,int end)
{
//一开始想的是用栈来处理 但是发现双指针更容易一些
for(int i=startIndex,j=end;i<j;i++,j--)
{
if(s.charAt(i)!=s.charAt(j))
{
return false;
}
}
return true;
}
}其实可以不需要加终止条件,因为startIndex >= nums.size(),本层for循环本来也结束了,本来我们就要遍历整棵树。
有的同学可能担心不写终止条件会不会无限递归?
并不会,因为每次递归的下一层就是从i+1开始的。
如果要写终止条件,注意:result.push_back(path);要放在终止条件的上面,如下
class Solution {
List<List<Integer>> result=new ArrayList<>();
List<Integer> temp=new ArrayList<>();
public List<List<Integer>> subsetsWithDup(int[] nums) {
Arrays.sort(nums);
backtracking(nums,0);
return result;
}
public void backtracking(int[] nums,int start)
{
//没有终止条件限定就是到达每一个叶子节点时都将temp放入结果
result.add(new ArrayList(temp));
for(int i=start;i<nums.length;i++)
{
if(i>start&&nums[i]==nums[i-1])
{
//i==start表示是同一枝 还未同层扩展
continue;//同层不能有重复
}else{
temp.add(nums[i]);
backtracking(nums,i+1);
temp.remove(temp.size()-1);//回溯
}
}
return;
}
}
class Solution {
List<List<Integer>> result=new ArrayList<>();
List<Integer> temp=new ArrayList<>();
public List<List<Integer>> findSubsequences(int[] nums) {
// Arrays.sort(nums);
backtracking(nums,0);
return result;
}
public void backtracking(int[] nums,int startindex)
{
if(temp.size()>=2)//用temp.size()控制深度
{
//因为在每次操作的前面
result.add(new ArrayList(temp));
}
//used是局部创建的 只负责同层去重 向下延伸到新的结点时 会重新new一个
Set<Integer> used=new HashSet<>();//用used判定是否用过元素
for(int i=startindex;i<nums.length;i++)
{
if(used.contains(nums[i]))//同层去重
continue;
if(temp.size()==0||nums[i]>=temp.get(temp.size()-1)){
temp.add(nums[i]);
used.add(nums[i]); // 记录这个元素在本层已经使用过
backtracking(nums,i+1);
temp.removeLast();
}
}
return;
}
}在 backtrack 函数的循环中,我们遍历整个 nums 数组。对于每个 nums[i],我们首先检查 used[i] 是否为 true。如果为 true,这意味着 nums[i] 已经在当前排列中,因此我们跳过它,继续检查下一个数字。

class Solution {
List<List<Integer>> result = new ArrayList<>();
List<Integer> temp = new ArrayList<>();
public List<List<Integer>> permute(int[] nums) {
if (nums == null || nums.length == 0)
return result;
boolean[] used = new boolean[nums.length]; // 增加一个用于跟踪元素是否被使用的布尔数组
backtrack(nums, used);
return result;
}
private void backtrack(int[] nums, boolean[] used) {
if (temp.size() == nums.length) {
result.add(new ArrayList<>(temp)); // 完成一种排列
return;
}
for (int i = 0; i < nums.length; i++) {
if (!used[i]) { // 检查这个元素是否已经被使用
used[i] = true;
temp.add(nums[i]);
backtrack(nums, used); // 继续递归填充下一个数字
temp.remove(temp.size() - 1); // 回溯,移除最后一个元素,尝试其他可能性
used[i] = false; // 标记为未使用
}
}
}
}
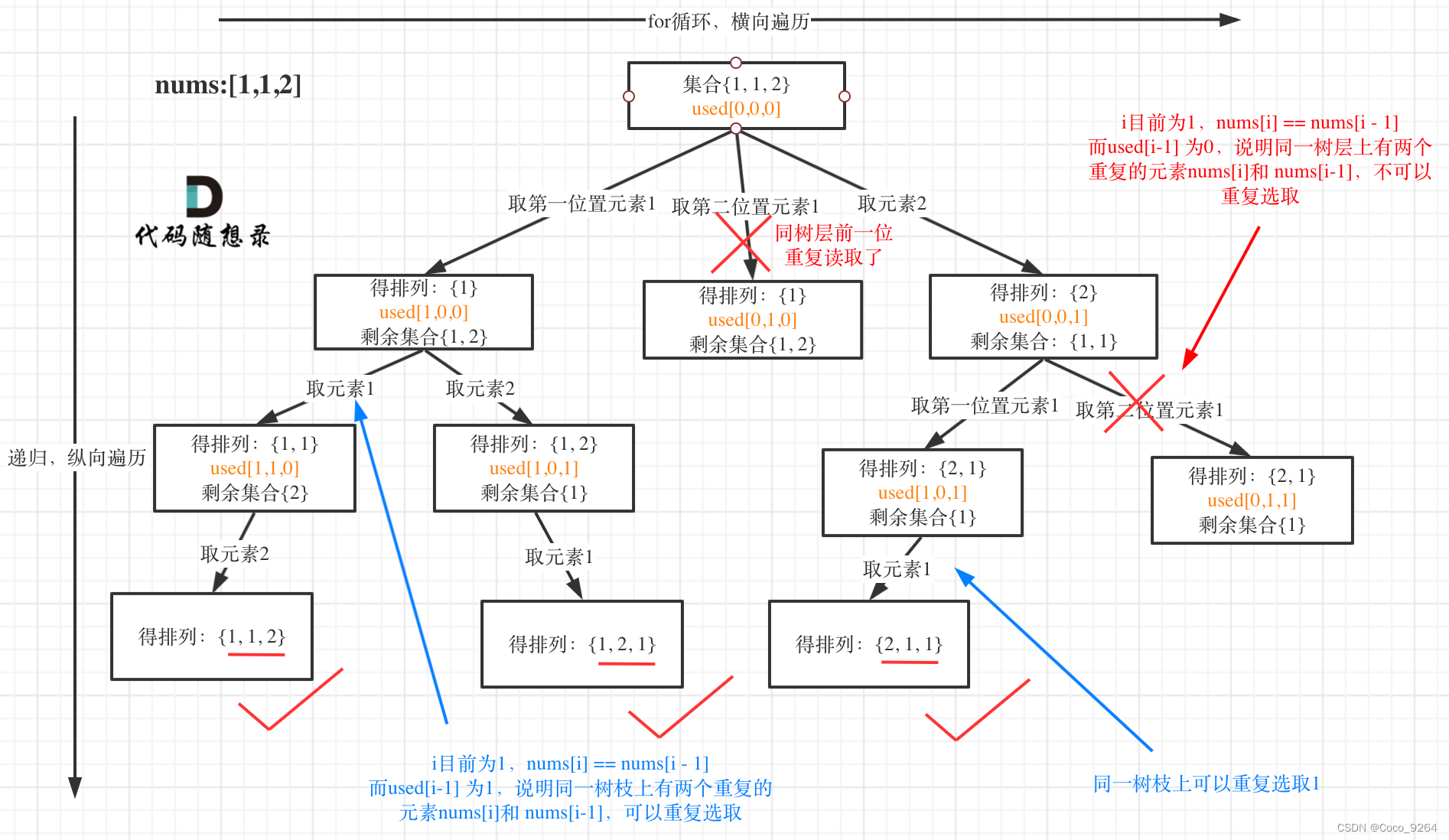
当遇到一个与前一个元素相同的元素时,只有在前一个元素已被使用的情况下才继续递归。这样可以防止生成重复的排列。前一个元素未被使用说明是同一层,不能







 本文解释了Java中类型推断和钻石操作符如何简化List<List<Integer>>的创建,并通过示例展示了在LeetCode题目中如何使用递归和剪枝策略解决组合问题,包括元素组合、回文串分割和子序列查找等。
本文解释了Java中类型推断和钻石操作符如何简化List<List<Integer>>的创建,并通过示例展示了在LeetCode题目中如何使用递归和剪枝策略解决组合问题,包括元素组合、回文串分割和子序列查找等。
















 634
634

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








