了解了梯度下降的知识,不在代码上体现怎么可以呢?
上代码,先看第一个,
经典房价问题:
# 导入需要用到的库
import numpy as np
import matplotlib.pyplot as plt
# 定义存储输入数据(x)和目标数据(y)的数组
x, y = [], []
# 遍历数据集,变量sample对应的正是一个个样本
for sample in open("C:\\Users\\贺旭伟\\Desktop\\shujuji.txt.txt", 'r'):
_x, _y = sample.split(",")
# 将字符串数据转化为浮点数
x.append(float(_x))
y.append(float(_y))
# 读取完数据后,将他们转化为Numpy数组以方便进一步的处理
x, y = np.array(x), np.array(y)
# 标准化
x = (x - x.mean()) / x.std()
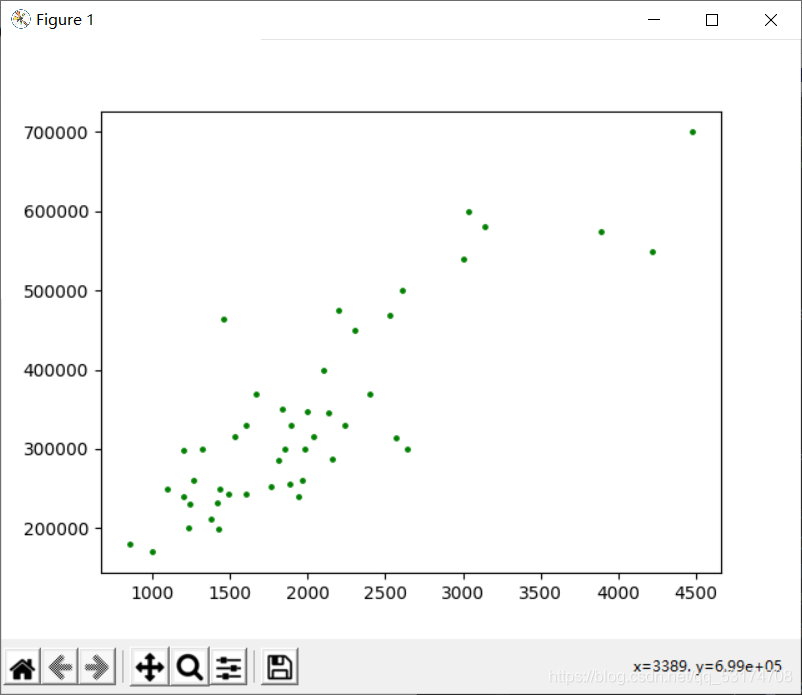
# 将原始数据集以散点的形式画出
plt.figure()
plt.scatter(x, y, c="g", s=6)
plt.show()
# (-2,4)这个区间上取100个点作为画图的基础
x0 = np.linspace(-2, 4, 100)
# 利用Numpy的函数定义训练并返回多项式回归模型的次数
# deg参数代表着模型参数中的n,即模型中多项式的次数
# 返回的模型能够根据输入的x(默认是x0),返回预测的y
def get_model(deg):
return lambda input_x=x0: np.polyval(np.polyfit(x, y ,deg), input_x)
# 根据参数n、输入的x,y返回相对应的损失
def get_cost(deg, input_x,input_y):
return 0.5 * ((get_model(deg)(input_x) - input_y) ** 2).sum()
# 定义测试函数集并根据它进行各种实验
test_set = (1, 4, 10)
for d in test_set:
# 输出损失
print(get_cost(d, x, y))
# 画出相应的图像
plt.scatter(x, y, c="g", s=20)
for d in test_set:
plt.plot(x0, get_model(d)(), label="degree = {}".format(d))
# 将横轴和纵轴的范围分别限制在(-2,4)和(10^5,10^6)
plt.xlim(-2, 4)
plt.ylim(1e5, 1e6)
# 调用legend方法使曲线对应的label正确显示
plt.legend()
plt.show()
给数据集(在桌面创建txt文件即可,注意修改代码中的路径):
2104,399900
1600,329900
2400,369000
1416,232000
3000,539900
1985,299900
1534,314900
1427,198999
1380,212000
1494,242500
1940,239999
2000,347000
1890,329999
4478,699900
1268,259900
2300,449900
1320,299900
1236,199900
2609,499998
3031,599000
1767,252900
1888,255000
1604,242900
1962,259900
3890,573900
1100,249900
1458,464500
2526,469000
2200,475000
2637,299900
1839,349900
1000,169900
2040,314900
3137,579900
1811,285900
1437,249900
1239,229900
2132,345000
4215,549000
2162,287000
1664,368500
2238,329900
2567,314000
1200,299000
852,179900
1852,299900
1203,239500
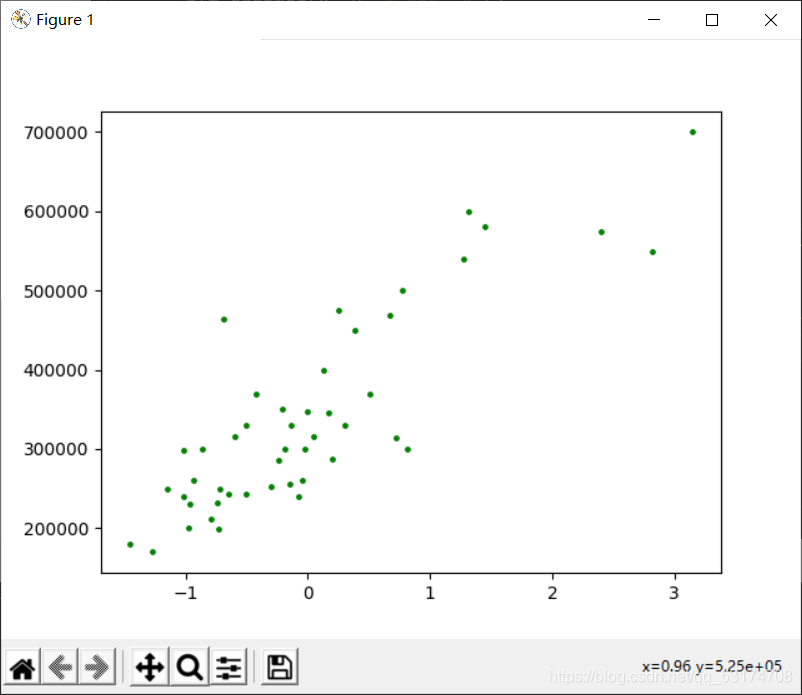
这是代码跑出来的图。下面详细讲解:
首先导入numpy和matplotlib两个库。用一个循环来把文本中的数据赋值给_x和_y,
然后把x和y从列表转为numpy中的一维数组。x是房子面积,y是房价。
先画一个散点图,对应于xy,就是我们的第一个图。可以看到第一个图和第二个图的区别就是横坐标不一样,原因是第一个图没有标准化,你可能不太理解为什么要标准。下面给出标准化的作用:
复制粘贴人家的不好,我给出链接,哈哈,标准化的意义和方法
图二和图三中横轴是标准化之后的面积,纵轴是房子的价格。
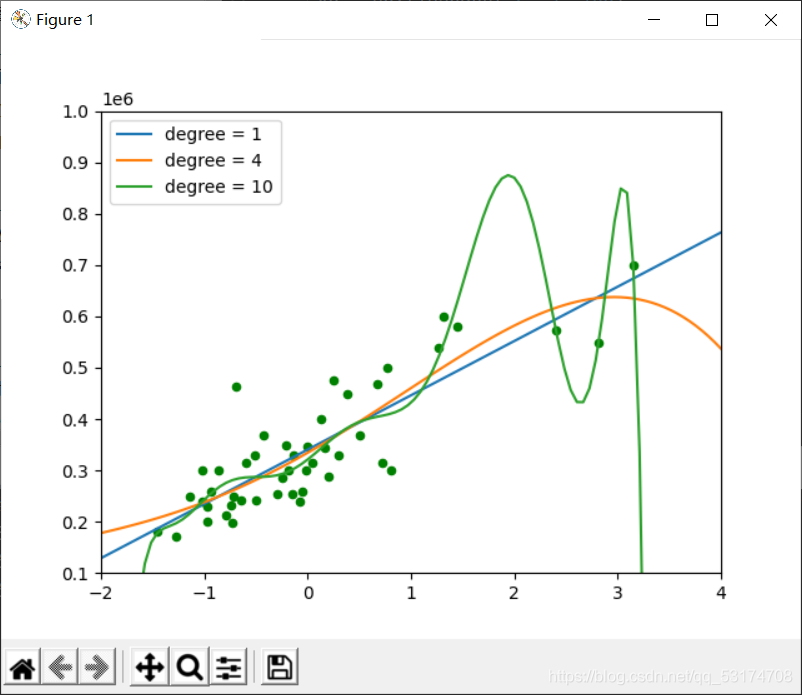
为了画出图三的线:
模型损失函数是平方损失函数也就是所谓的欧式距离,这里的目的是要将损失函数最小化
利用Numpy训练和优化
模型的数学表达式为:
f(x|p;n)=p0xn+p1x(n-1)+…+pn-1x+pn
L(p;n)=0.5∑[f(x|p;n)-y]^2
可能会卡在numpy的几个拟合函数上,给链接
return lambda input_x=x0: np.polyval(np.polyfit(x, y ,deg), input_x)
可能这个函数不太明白,我简单讲讲,lambda是python的匿名函数,没啥好说的,右面的两个函数,从内到外:先说np.polyfit,它有三个参数,x和y就是需要拟合的数据,deg是需要拟合出函数的阶数,比如deg=5,那么就会输出六个数(假如是1,2,3,4,5,6),则代表拟合出的函数是1x5+2x4+3x3+4x2+5x1+6。就是这个意思。而polyval函数的意思是把第二个参数x带入得到的函数里,求值。挺详细吧,还没听懂就评论区留言吧,一起学习。
还有一点需要注意:
def get_model(deg):
return lambda input_x=x0: np.polyval(np.polyfit(x, y ,deg), input_x)
def get_cost(deg, input_x,input_y):
return 0.5 * ((get_model(deg)(input_x) - input_y) ** 2).sum()
第一个函数返回的是一个函数(叫模型也行),第二个函数用到了第一个函数返回的函数(模型),第二个函数得到的就是平方损失函数(我觉得和代价函数出不多,仅本人愚见)。
然后代码就没什么讲的了,这个代码没有用到梯度下降,所以我们来看第二个代码,用梯度下降找代价函数最低点。
梯度下降问题
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.axes3d import Axes3D
#f(w1,w2) = w1^2 + w2^2 + 2*w1*w2 + 500
def targetFunction(W):
w1, w2 = W
return w1 ** 2 + w2 ** 2 + 2 * w1 * w2 + 500
def gradientFunction(W):#梯度功能
w1, w2 = W
w1_grad = 2 * w1 + 2 * w2
w2_grad = 2 * w2 + 2 * w1
return np.array([w1_grad, w2_grad])#以二维数组的形式返回梯度
def batch_gradient_distance(targetFunc,gradientFunc,init_W,learning_rate = 0.01,tolerance = 0.0000001): #核心算法
W = init_W #w是随机生成的二维数组
target_value = targetFunc(W) #生成目标函数
counts = 0 #开始统计
while counts < 5000:
gradient = gradientFunc(W)#计算出梯度
next_W = W - gradient * learning_rate#新的二维数组等于原有的减去梯度*学习率
next_target_value = targetFunc(next_W)#创建新的目标函数
if abs(next_target_value - target_value)<tolerance:
print("此结果经过了", counts, "次循环")
return next_W
else:
W, target_value = next_W, next_target_value
counts += 1
else:
print("没有取到极值点")
if __name__ == '__main__':
np.random.seed(0) #保证每次运行随机出来的结果一致
init_W = np.array([np.random.random(),np.random.random()]) #随机初始的w1,创建一个随机的二维数组
w1,w2 = batch_gradient_distance(targetFunction,gradientFunction,init_W)
print(w1,w2)
x1=np.arange(-10,11,1) #为了绘制函数的原图像
x2=np.arange(-10,11,1)
x1, x2 = np.meshgrid(x1, x2) # meshgrid :3D坐标系
z=x1**2 + x2**2 + 2*x1*x2+500
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(x1, x2, z) #绘制3D坐标系中的函数图像
ax.scatter(w1,w2, targetFunction([w1,w2]), s=50, c='red') #绘制已经找到的极值点
ax.legend() #使坐标系为网格状
plt.show() #显示
这个代码为了避免进入局部最优解问题,我直接给出函数f(x,y)=x2+y2+2xy+500。找出的最优解的图像为:
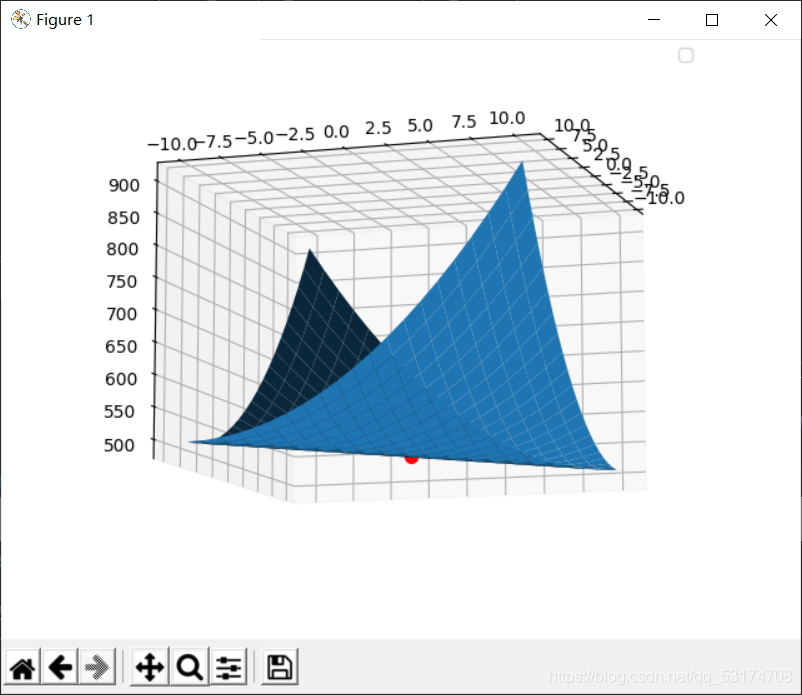
图中的红点就是最低点。
接下来就要用到偏导的知识了:
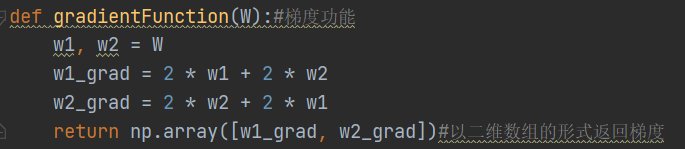
还有一个点要注意:






















 1008
1008

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








