2021-04-28

机器学习
上一节，我们已经知道了什么是代价函数，这次，我们讲具体的用法：
如图：左边是假设函数，右边是代价函数，暂且令纵截距为0，那么每一个斜率，都会产生一个代价函数上的一个值，

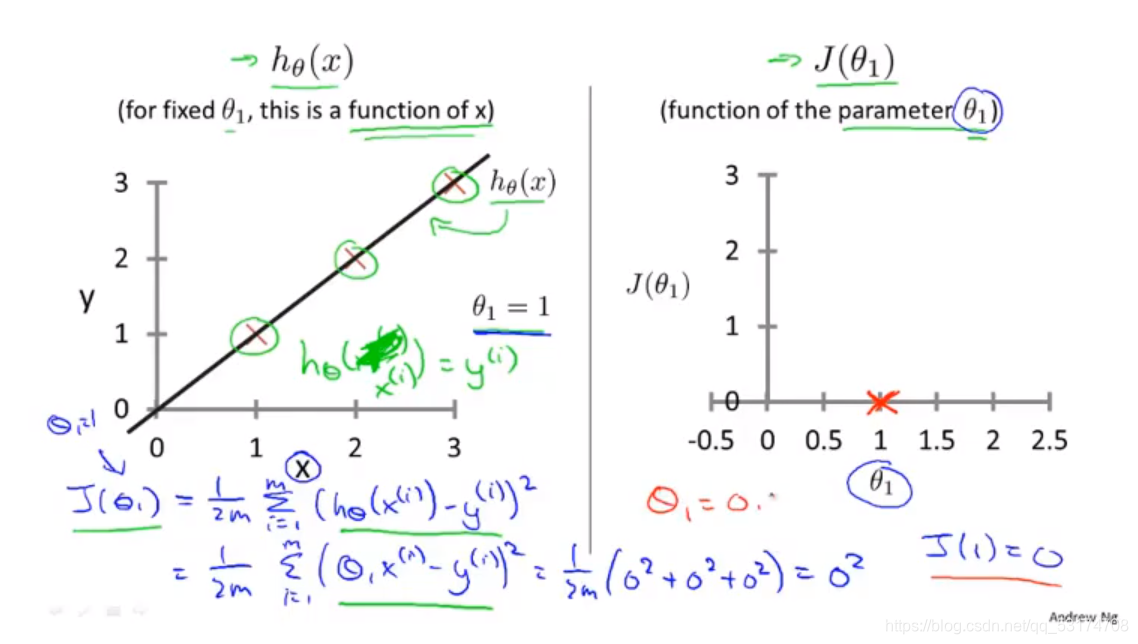
然后我们对斜率重复取值，结果便会在代价函数的图中画许多的点，连接起来后，讲代价函数的图像画了出来，横坐标是斜率，如图:

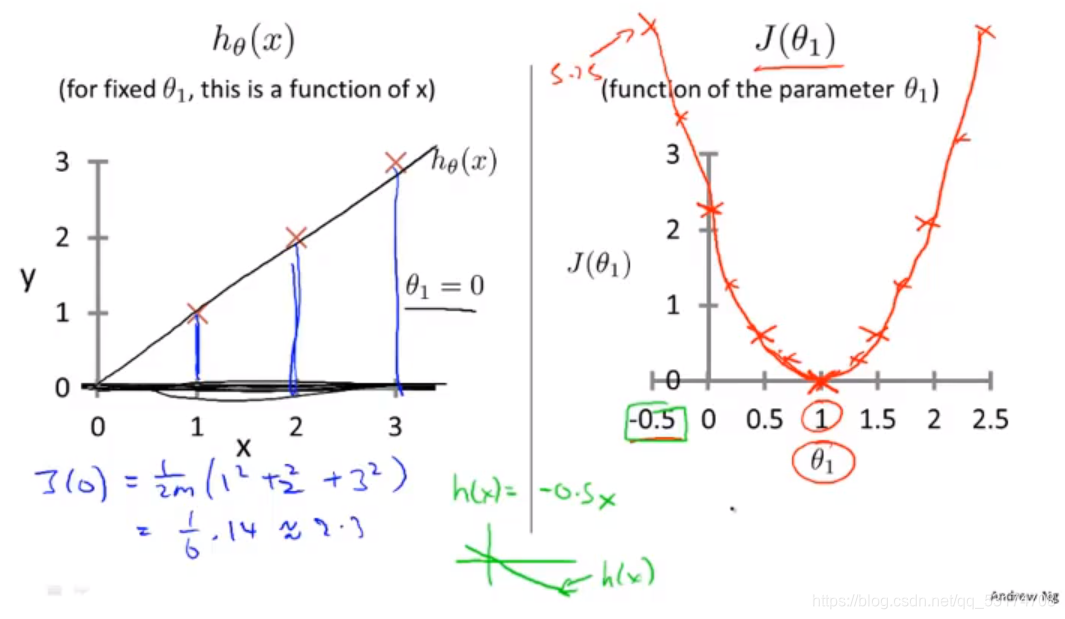
很明显，为了最拟合，便要让代价函数最小，从右图中看出斜率为1是最合适。
接下来我们保留纵截距和斜率，这样我们的代价函数便会与两个自变量有关，一个自变量可以得到一条曲线，两个自变量我们便可以得到一个立体图，如下：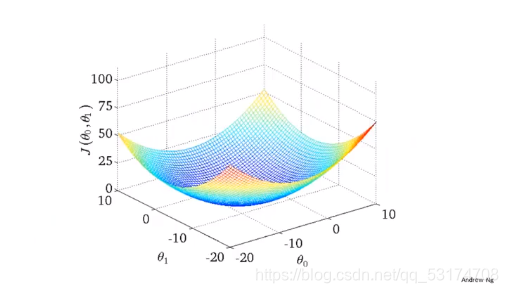
这只是一种情况，不是所有的代价函数曲线都是这样，在这个3d图中，我们要找到最低点，找点的过程种，我们便要用到偏导数的方法。
首先，为了便于理解，我们的吴恩达老师将3d图转化成了等高线图。

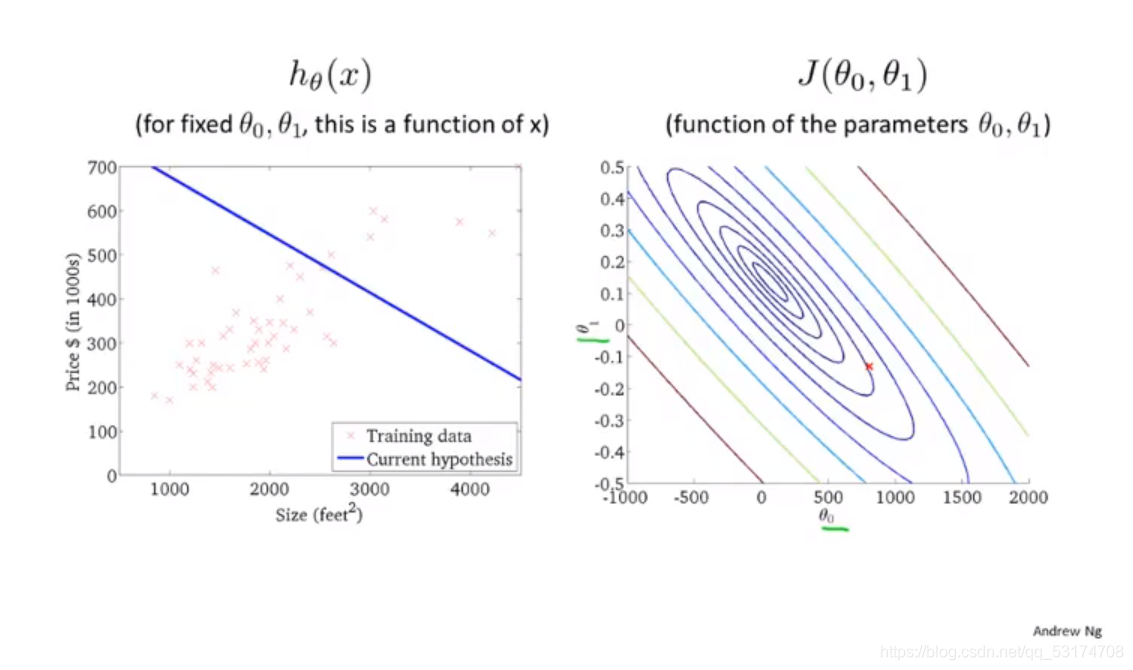
登高线图上的没一个点都代表了一个纵截距和斜率，其实很容易想到，在等高线的最低点，也就是中心位置，代价函数最小，函数拟合的最好，我们需要一个高效的算法来找到这个点。用到的方法便是偏导数中的梯度下降法。
视频分享

为了便于理解梯度下降，我们先看二维，如图，三维的偏导对应二维的导数，也就是斜率，那么公式的意思就是沿着斜率下降一定（学习率）的距离，直到找到最低点。

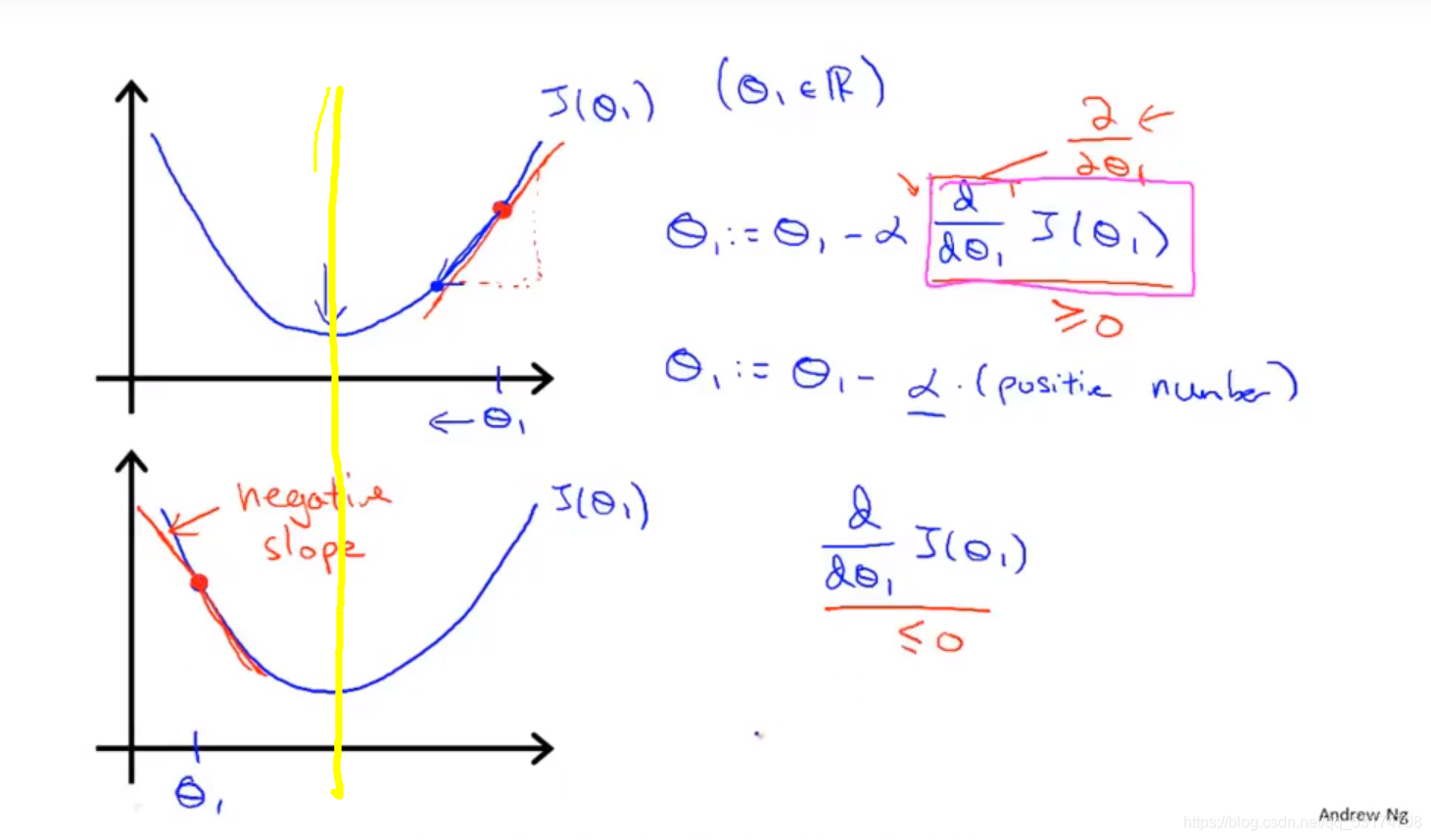
我刚开始的困惑是既然下降的距离是一定的，为什么总能找到最低点，尤其是三维的时候，沿两个方向不是同等程度的下降吗？按理说是一条直线啊，知道我看了二维的图，如上图，仔细思考我画的黄线的意义，提示1：线上的点过了黄线斜率会变号。提示2：过了黄线后，会折返。
还有一点新人不理解，就是为什么无论学习率多大，一定能找到最低点，你应该想，在最低点时，斜率为0，点的位置就不动了。