原码,反码,补码,傻傻分不清?

什么是原码,反码,补码?

非常重要!!!

 计算机计算方式:

 原码最左边的符号位,0为正数,1为负数;

 将十进制转为二进制进行计算(原码),但是原码存在弊端,无法计算负数;

 因此出现了反码用来计算负数,反码就是将原码的0变成1,1变成0;

 但是在计算加法等方式时,一旦最终值大于负数,那么就会出现一个[1]的偏差;

 所以这个时候就出现了补码,补码就是在反码的基础上加[1];

 注意:因为补码加了[1],所以负数多出了一个数字[-128],并且它没有原码和反码;

 而正数的一个字节则最大为[127];

 注意:正数的原码、反码和补码都是一样的;负数的补码等于补码加 1,负数的反码等于补码 -1;

 使用:当发生强制类型转换时,会自动去除多余的位数;

     如:int强转为byte时,系统会自动把多出来的3个字节全部清除,不论是否有数据存在,因此强转会出现数据溢出的情况;

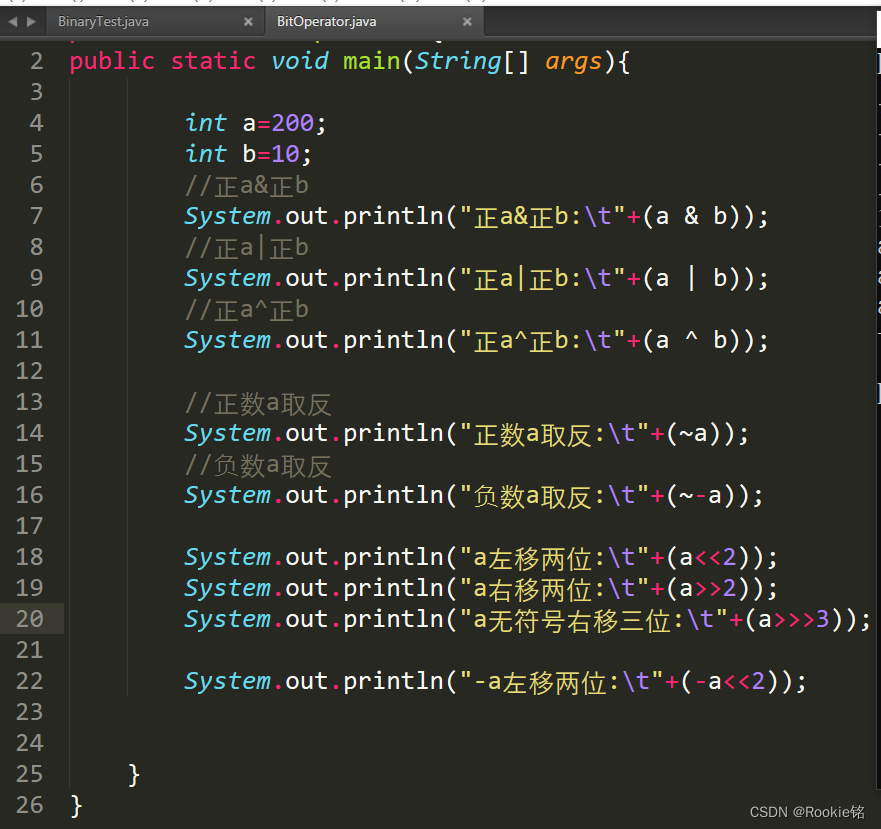
int a = 200;

int b = 10;

 按位与的运算规则:0为false,1为true;

 在计算的时候, 只有a和b二进制形式对应的数字位都为[1],计算之后的二进制数的那一位才能是1,否则就是0;

 说一下为什么二进制数位这么长,那是因为一个int数字占4字节,一个字节由8位二进制构成!!!

 以 int a = 200;int b = 10;举例

 如:  int a = 200的二进制数为:0000 0000 0000 0000 0000 0000 1100 1000,

      int b = 10 的二进制数为:0000 0000 0000 0000 0000 0000 0000 1010,

     那么 a & b 时,两个二进制数依照对应的位数一一对应,

     正数三码合一:

     可以得出结果的原码:0000 0000 0000 0000 0000 0000 0000 1000,

     最后换算为十进制数为:8;

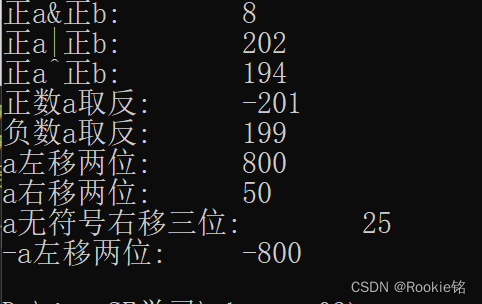
     System.out.println(a & b);//8

    

 按位或的运算规则:0为false,1为true,

 但是在计算的时候,[或]只有a和b二进制形式对应的数字位只需要其中有一个为[1],

         那么计算之后的二进制数的那一位就是1,否则就是0;

 如:int a = 200 与 int b = 10 的时候, a | b

         正数三码合一:

         可以得出结果的原码:0000 0000 0000 0000 0000 0000 1100 1010,

     最后换算为十进制数为:202;

     System.out.println(a | b);//202

     

 按位异或的运算规则:0为false,1为true,

 但是在计算的时候,[异或]只有a和b二进制形式对应的数字位其中一个为[1],另一个为[0],

         那么计算之后的二进制数的那一位才是1,否则就是0;

 如:int a = 200 与 int b = 10 的时候, a ^ b

         正数三码合一:

         可以得出结果原码:0000 0000 0000 0000 0000 0000 1100 0010,

     最后换算为十进制数为:194;

     System.out.println(a ^ b);//194

    

 按位取反的运算规则:0为false,1为true,

 但是在计算的时候,[取反]时,[0]变[1],[1]变[0]

 如:int a = 200

         正数三码合一:

         可以得出 a的补码:0000 0000 0000 0000 0000 0000 1100 1000,

         然后进行 取反操作, ~a,

         运算后的补码:    1111 1111 1111 1111 1111 1111 0011 0111,

         而前面说到过,反码等于(它的)补码-1

         可以得出 a的反码:1111 1111 1111 1111 1111 1111 0011 0110,

         可以得出 a的原码:1000 0000 0000 0000 0000 0000 1100 1001,

     最后换算为十进制数为:-201;

     System.out.println(~a);//-201

    

    

前面说了正数的三码都是一样的,但是负数可不同咯;

     int a = -200,

         可以得出 a的原码:1000 0000 0000 0000 0000 0000 1100 1000,

         可以得出 a的反码:1111 1111 1111 1111 1111 1111 0011 0111,   

         可以得出 a的补码:1111 1111 1111 1111 1111 1111 0011 1000,

         然后再进行 取反   ~-a,

         运算后的补码:   0000 0000 0000 0000 0000 0000 1100 0111,

         正数,三码合一:

         a的原码就是:    0000 0000 0000 0000 0000 0000 1100 0111,

     最后换算为十进制数为:199;

     System.out.println(~a);//199

 注意:默认的移动规则实则就是一句话,

         左移一位翻一倍,如200变400;

         右移一位缩一倍,如200变100;

         而无符号右移,则是不论其最左边一位是正数的[0]还是负数的[1],一律给它补上[0];

        

 依旧是 int a = 200;举例

 左移(<<)的运算规则:向左移动,低位补0,

         如:并且把它左移[2]位,

         那么它的二进制数将会由:0000 0000 0000 0000 0000 0000 1100 1000,

                          变成:0000 0000 0000 0000 0000 0011 0010 0000,

     最后换算为十进制数为:800;

     System.out.println(a << 2);

    

 右移的运算规则与左移相似,只是他的高位补0或1,

         也就是说如果二进制数为正数时,最左边的位数为[0],那么我们就需要补[0],

         如果是负数那么就是补[1],

         而左边第二位的数值位直接用[0]替代;

         那么它的二进制数将会由:0000 0000 0000 0000 0000 0000 1100 1000,

                                     变成:0000 0000 0000 0000 0000 0000 0011 0010,

         最后换算为十进制数为:50;

         System.out.println(a >> 2);

        

 无符号右移(>>>),运算规则就是向右移动,高位补[0];

         那么它的二进制数将会由:0000 0000 0000 0000 0000 0000 1100 1000,

                                     变成:0000 0000 0000 0000 0000 0000 0001 1001,

         最后换算为十进制数为:25;

         System.out.println(a >>> 3);

        

虽然不太喜欢算负数,但还是举个栗子吧.

int a = -200;

    之前算过 a为负数时的原码为: 1000 0000 0000 0000 0000 0000 1100 1000, 

    左移[2]位,

         可以得出 a的左移后的原码:1000 0000 0000 0000 0000 0011 0010 0000,(写到这其实就够了)

         可以得出 a的左移后的反码:1111 1111 1111 1111 1111 1100 1101 1111,   

         可以得出 a的左移后的补码:1111 1111 1111 1111 1111 1100 1110 0000,

         最后换算为十进制数为:-800;

代码图:

        

 结果: