
判断一棵二叉树是否为左右对称,及从根部开始看是否在左右相对称的节点上的值是否相等,因此我们需要将这个二叉树从上到下依次遍历。
在前序,中序,后序三种顺序结构中,要选择前序遍历。为什么呢?
因为要是比较这个二叉树是否对称,就不是单纯的依次递归,而是从根部开始左右子根依次遍历,如果在开始的时候两个节点对应的值就不相等,那么我们就没有再继续遍历的必要了。如果选择其他的遍历方法,那么就是遍历以后再进行比较,就会比较麻烦。

在根部比较左右子根,如果相同,则继续向下比较,继续向两个子根向下
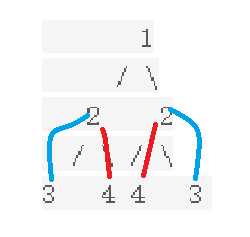
如图,将第二层的左子根的左根和右子根的右根比较,左根的右子根和右根的左子根比较,如果完全相同,则该二叉树是镜像二叉树
bool _cheakSame(struct TreeNode* left,struct TreeNode* right)//对于判断左右子根是否相等
{
if(left==NULL&&right==NULL)
{
return true;
}
if(left==NULL||right==NULL)
{
return false;
}
if(left->val!=right->val)
{
return false;
}
else
{
return _cheakSame(left->left,right->right)&&
_cheakSame(left->right,right->left);
}
}
bool isSymmetric(struct TreeNode* root){
if(root==NULL)//如果是空,则对称
{
return true;
}
return _cheakSame(root->left,root->right);
}

如图即为该函数递归的思路
总结:
1.在遇到二叉树当中的数值判断问题,应采用前序的方法来遍历,先判断数据,再决定是否继续向下
2.在写判断两节点是否相等时,会有很多种情况,例如都是空,一个空一个不空,如果两个节点对应的数据相等,那么该怎么向下遍历,如何确定遍历停止的条件都是问题
要想解决这种情况特别多的问题,其实最好的方法就是反向思考,就像该思路中写的,先判断两个节点是否同时为空,如果同时为空,那么就相等,如果有一个不为空,该情况下,我们不去讨论究竟谁是空,只是说leftNULL||rightNULL,该意思就是只要其中有一个为空,结果就是假
如果判断的两个节点相等呢,该怎么说下面的节点呢,因此我们反向来说,先把不相等的情况摘出来,该情况下结果为假,否则的话就根据递归继续向下啦
























 579
579

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








