目录
什么叫策略模式
策略模式(Strategy Pattern)是一种行为型设计模式,它定义了一簇算法、封装每个算法,并使它们可互相替换,以便客户端可以在运行时选择不同的算法来解决特定的问题。策略模式将算法的选择从具体的类中分离出来,使得算法的变化不会影响到使用算法的客户端。
策略模式有助于遵循开闭原则,因为它允许在不修改现有代码的情况下添加新的策略。
策略模式的作用
分离算法的定义和使用:策略模式将算法的具体实现与算法的使用分离开来,使得客户端代码不需要关心具体的算法细节。这样,客户端代码可以专注于高层逻辑,而不会受到底层算法的影响。
提高代码的灵活性:通过将算法封装成独立的策略类,策略模式使得在运行时可以轻松地切换不同的算法。这样,系统可以根据需要动态地选择最合适的算法,而无需修改客户端代码。
易于扩展:策略模式使得添加新的算法变得相对简单。只需创建新的具体策略类,并将其引入到上下文中,而不必修改现有的代码。
降低耦合度:策略模式通过将算法的选择从客户端代码中分离出来,降低了客户端代码与具体算法的耦合度。这使得客户端代码更加独立、可维护和易于测试。
复用性:策略模式将算法封装成独立的类,可以在不同的上下文中重用相同的策略。这有助于提高代码的复用性。
可读性:策略模式提供了一种清晰的方式来组织和管理不同的算法实现,使得代码更加可读和易于理解。
策略模式的特征
策略接口(Strategy Interface):定义了一组算法的通用接口,通常包括一个或多个抽象方法,表示具体策略类应该实现的操作。
具体策略类(Concrete Strategies):实现策略接口,提供具体的算法实现。
上下文类(Context):包含一个策略接口的引用,可以动态切换不同的具体策略。上下文类负责将具体的算法委派给策略对象执行。
策略模式的应用场景
策略模式在软件开发中有许多常见的应用场景,特别是在需要根据不同情况选择不同算法或策略的情况下,比如:
排序算法:对于排序操作,可以使用策略模式来实现不同的排序算法,例如冒泡排序、快速排序、归并排序等,以便在运行时选择最适合的排序策略。
图像处理:图像处理应用通常需要应用不同的滤镜或变换算法。策略模式可以用来封装这些算法,使用户能够选择不同的处理策略。
支付方式:在电子商务应用中,不同的支付方式(信用卡、微信、支付宝等)可以视为不同的支付策略。策略模式可以用来处理不同的支付方式。
策略模式的实现
定义策略接口
首先,定义一个策略接口,它声明了一组算法的通用方法或操作。这个接口将作为具体策略类的基础。例如,假设我们要实现不同的排序策略,可以定义一个 SortStrategy 接口,包含一个 sort 方法。
public interface SortStrategy {
void sort(int[] arr);
}创建具体策略类
接下来,实现策略接口的具体策略类,每个具体策略类都包含了特定算法的实现。例如,我们可以创建 BubbleSortStrategy 和 InsertionSortStrategy 等具体策略类。
//冒泡排序策略类
public class BubbleSortStrategy implements SortStrategy {
@Override
public void sort(int[] arr) {
int n = arr.length;
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
// 交换 data[j] 和 data[j+1] 的位置
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
}//快速排序策略类
public class InsertionSortStrategy implements SortStrategy {
@Override
public void sort(int[] arr) {
int n = arr.length;
for (int i = 1; i < n; i++) {
int key = arr[i];
int j = i - 1;
// 将 arr[i] 插入到已排序序列中的合适位置
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
}
创建上下文类
上下文类包含一个对策略接口的引用,并且可以在运行时切换不同的策略。上下文类通常包括一个设置策略的方法以及使用策略的方法。
public class Sorter {
//排序策略
private SortStrategy strategy;
public Sorter(SortStrategy strategy) {
this.strategy = strategy;
}
// 设置新的排序策略
public void setStrategy(SortStrategy strategy) {
this.strategy = strategy;
}
// 使用当前策略来执行排序
public void performSort(int[] arr) {
strategy.sort(arr);
}
}进行测试
public class Test {
public static void main(String[] args) {
int[] arr = {5, 2, 8, 1, 9};
// 创建上下文对象并设置初始策略
Sorter sorter = new Sorter(new BubbleSortStrategy());
// 使用冒泡排序策略进行排序
sorter.performSort(arr);
System.out.println("冒泡排序结果:" + Arrays.toString(arr));
// 切换到插入排序策略
sorter.setStrategy(new InsertionSortStrategy());
// 使用新策略进行排序
sorter.performSort(arr);
System.out.println("插入排序结果:" + Arrays.toString(arr));
}
}结果为:
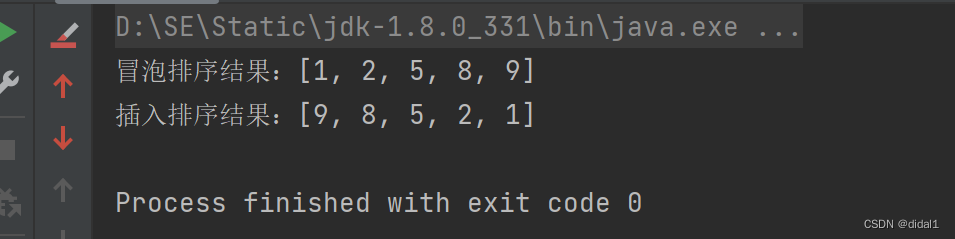
可以看到,排序的结果是完全符合要求的。
总结
总的来说,其实我们可以把策略模式就看成是封装了 if 或 switch,主要是策略模式的扩展性更强,能够降低耦合性,符合开闭原则。





 策略模式是一种行为型设计模式,它通过定义策略接口、具体策略类和上下文类,实现算法的灵活替换。该模式有助于提高代码的可读性、灵活性和扩展性,同时降低耦合度,支持开闭原则。应用示例包括排序算法、图像处理和支付方式选择。
策略模式是一种行为型设计模式,它通过定义策略接口、具体策略类和上下文类,实现算法的灵活替换。该模式有助于提高代码的可读性、灵活性和扩展性,同时降低耦合度,支持开闭原则。应用示例包括排序算法、图像处理和支付方式选择。

















 430
430

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










