3.16《LeetCode零基础指南》第九讲递归学习反思

一、

938. 二叉搜索树的范围和

难度简单279

给定二叉搜索树的根结点 root，返回值位于范围 [low, high] 之间的所有结点的值的和。

示例 1：

输入：root = [10,5,15,3,7,null,18], low = 7, high = 15
输出：32

示例 2：

输入：root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10
输出：23

提示：

• 树中节点数目在范围 [1, 2 * 104] 内
• 1 <= Node.val <= 105
• 1 <= low <= high <= 105
• 所有 Node.val 互不相同

深度暴力搜索就完了：

class Solution {
public:
    int rangeSumBST(TreeNode* root, int low, int high) {
        if(!root)return 0;
        if(root->val<=high&&root->val>=low)
        {
            return root->val+rangeSumBST(root->left,low,high)+rangeSumBST(root->right,low,high);
        }
        return rangeSumBST(root->left,low,high)+rangeSumBST(root->right,low,high);
    }
};

**广度搜索：（涉及队列，之后看）**

---------------------------------------------------------------------------------------------------------------------------------

二、

剑指 Offer 55 - I. 二叉树的深度

难度简单172

输入一棵二叉树的根节点，求该树的深度。从根节点到叶节点依次经过的节点（含根、叶节点）形成树的一条路径，最长路径的长度为树的深度。

例如：

给定二叉树 [3,9,20,null,null,15,7]，

    3
   / \
  9  20
    /  \
   15   7

返回它的最大深度 3 。

递归就完了：

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(!root)return 0;
        else
        {
            return 1+max(maxDepth(root->left),maxDepth(root->right));
        }
    }
};

广度搜索：

int maxDepth(TreeNode* root) {
    if (root == nullptr)
        return 0;
    queue<TreeNode*> que;
    que.push(root);
    int depth = 0;
    while (!que.empty()) {
        ++depth;
        int n = que.size();
        for (int i = 0; i < n; ++i) {
            TreeNode* node = que.front();
            que.pop();
            if (node->left)
                que.push(node->left);
            if (node->right)
                que.push(node->right);
        }
    }
    return depth;
}

---------------------------------------------------------------------------------------------------------------------------------

***三、

class Solution {
public:
    vector<vector<int>>result;
    vector<int>res;
    void huisu(vector<vector<int>>& graph,int x,int n)
    {
        if(x==n)
        {
            result.push_back(res);
        }
        for(auto y:graph[x])
        {
            res.push_back(y);
            huisu(graph,y,n);
            res.pop_back();
        }
    }
    vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
        res.push_back(0);
        huisu(graph,0,graph.size()-1);
        return result;
    }
};

226. 翻转二叉树

难度简单1203

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

示例 2：

输入：root = [2,1,3]
输出：[2,3,1]

示例 3：

输入：root = []
输出：[]

递归：

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if(root==nullptr)return root;
        swap(root->left,root->right);
        invertTree(root->left);
        invertTree(root->right);
        return root;
    }
};

深度优先：

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if(root==nullptr)return root;
        stack<TreeNode*> st;
        st.push(root);
        while(!st.empty())
        {
            TreeNode*node=st.top();
            st.pop();
            swap(node->left,node->right);
            if(node->left)st.push(node->left);
            if(node->right)st.push(node->right);
        }
        return root;
    }
};

---------------------------------------------------------------------------------------------------------------------------------

***四、

797. 所有可能的路径

难度中等262收藏分享切换为英文接收动态反馈

给你一个有 n 个节点的 有向无环图（DAG），请你找出所有从节点 0 到节点 n-1 的路径并输出（不要求按特定顺序）

 graph[i] 是一个从节点 i 可以访问的所有节点的列表（即从节点 i 到节点 graph[i][j]存在一条有向边）。

示例 1：

输入：graph = [[1,2],[3],[3],[]]
输出：[[0,1,3],[0,2,3]]
解释：有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3

示例 2：

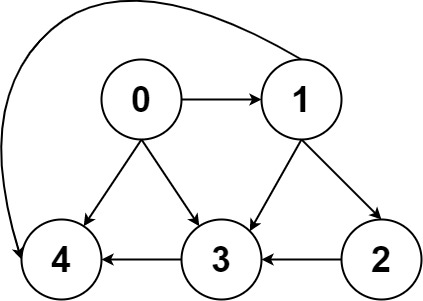
输入：graph = [[4,3,1],[3,2,4],[3],[4],[]]
输出：[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]

回溯法：

class Solution {
public:
    vector<vector<int>>result;
    vector<int>res;
    void huisu(vector<vector<int>>& graph,int x,int n)
    {
        if(x==n)
        {
            result.push_back(res);
        }
        for(auto y:graph[x])
        {
            res.push_back(y);
            huisu(graph,y,n);
            res.pop_back();
        }
    }
    vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
        res.push_back(0);
        huisu(graph,0,graph.size()-1);
        return result;
    }
};